LeetCode题练习与总结：求根节点到叶节点数字之和--129

news2024/10/6 1:37:51

一、题目描述

给你一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字。

每条从根节点到叶节点的路径都代表一个数字：

例如，从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。

计算从根节点到叶节点生成的 所有数字之和 。

叶节点 是指没有子节点的节点。

示例 1：

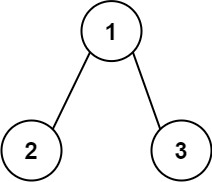
输入：root = [1,2,3]
输出：25
解释：
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此，数字总和 = 12 + 13 = 25

示例 2：

输入：root = [4,9,0,5,1]
输出：1026
解释：
从根到叶子节点路径 4->9->5 代表数字 495
从根到叶子节点路径 4->9->1 代表数字 491
从根到叶子节点路径 4->0 代表数字 40
因此，数字总和 = 495 + 491 + 40 = 1026

提示：

树中节点的数目在范围 [1, 1000] 内
0 <= Node.val <= 9
树的深度不超过 10

二、解题思路

这个问题是一个典型的深度优先搜索（DFS）问题。我们需要遍历整棵树，并且记录从根节点到当前节点的路径所形成的数字。当我们到达一个叶子节点时，就计算这条路径的数字，并将其累加到总和中。对于每一个非叶子节点，我们将其值乘以10然后加上其左子节点的值，再加上其右子节点的值，这样就可以得到所有从根节点到叶子节点路径的数字之和。

算法步骤：

初始化总和为0。
从根节点开始进行深度优先搜索。
在搜索过程中，记录下从根节点到当前节点的路径值。
当到达叶子节点时，将路径值加到总和中。
返回总和。

三、具体代码

class Solution {
    public int sumNumbers(TreeNode root) {
        return dfs(root, 0);
    }

    private int dfs(TreeNode node, int sum) {
        if (node == null) {
            return 0;
        }
        sum = sum * 10 + node.val;
        if (node.left == null && node.right == null) {
            return sum;
        }
        return dfs(node.left, sum) + dfs(node.right, sum);
    }
}

四、时间复杂度和空间复杂度

1. 时间复杂度

深度优先搜索（DFS）算法会遍历树中的每个节点一次。
对于每个节点，我们执行常数时间的操作，即计算当前路径值和递归调用。
因此，时间复杂度与树中节点的数量成正比，即 O(N)，其中 N 是树中节点的数量。

2. 空间复杂度

空间复杂度主要取决于递归调用栈的深度，这通常与树的高度成正比。
在最坏的情况下，树可能是高度平衡的，此时递归调用栈的深度为 O(logN)，其中 N 是树中节点的数量。
在最好的情况下，树完全不平衡，每个节点都只有一个子节点，此时递归调用栈的深度为 O(N)。
因此，空间复杂度在最坏情况下为 O(logN)，在最好情况下为 O(N)。

综上所述，该算法的时间复杂度为 O(N)，空间复杂度在最坏情况下为 O(logN)，在最好情况下为 O(N)。

五、总结知识点

递归：这是一种编程技巧，函数自己调用自己，用于解决可以分解为多个相似子问题的大问题。在这个问题中，我们使用递归来进行深度优先搜索（DFS）。
深度优先搜索（DFS）：这是一种用于遍历或搜索树或图的算法。在这个问题中，我们使用DFS来遍历二叉树的每个节点，并计算从根节点到叶节点的路径所代表的数字。
二叉树遍历：代码中实现的DFS实际上是二叉树的先序遍历（根-左-右），因为我们在访问左右子节点之前先访问当前节点。
路径累积：在递归过程中，我们将从根节点到当前节点的路径值传递给子节点，这是通过将当前路径值乘以10并加上当前节点的值来实现的。
回溯：虽然代码中没有显式的回溯步骤，但递归的本质包含了回溯的概念。一旦递归函数到达最深层并开始返回时，它会回溯到上一层，这是递归能够正常工作的关键。
边界条件处理：在递归函数中，我们首先检查当前节点是否为空，这是递归的边界条件，用于防止递归无限进行下去。
叶节点的判断：代码中通过检查当前节点是否没有子节点（即左右子节点都为空）来判断是否是叶节点。这是递归过程中的一个关键步骤，因为只有叶节点的路径值才会被累加到最终结果中。
函数参数和返回值：dfs 函数接受当前节点和当前路径值作为参数，并返回从根节点到叶节点的路径总和。这是递归函数设计的一个重要方面，确保了每次递归调用都能够正确地传递和处理数据。