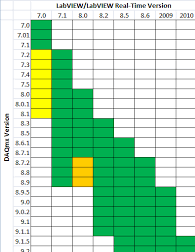
矩阵乘法是什么意思?
一种常见的观点是矩阵乘法缩放/旋转/倾斜几何平面:

NSDT工具推荐: Three.js AI纹理开发包 - YOLO合成数据生成器 - GLTF/GLB在线编辑 - 3D模型格式在线转换 - 可编程3D场景编辑器 - REVIT导出3D模型插件 - 3D模型语义搜索引擎 - Three.js虚拟轴心开发包 - 3D模型在线减面 - STL模型在线切割
这在第一次学习向量时很有用:向量输入,新向量输出。不幸的是,这可能导致过度依赖几何可视化。
如果有 20 个家庭来参加你的烧烤,你如何估计你需要的热狗?(嗯……20 个家庭,假设每个家庭 3 人,每人 2 个热狗……大约 20 * 3 * 2 = 120 个热狗。)
你可能不会想“哦,我需要一个邀请-家庭规模-饥饿棱镜的体积!”。对于大型矩阵,我不会考虑 500 维向量,只会考虑要修改的数据。
另一种开发是矩阵乘法组成线性运算。
这是技术上准确的定义:是的,矩阵乘法会产生一个由原始函数组成的新矩阵。但是,有时被操作的矩阵不是线性运算,而是一组向量或数据点。我们需要另一种直觉来了解正在发生的事情。
我将以软件开发人员的观点来看待这个问题:
矩阵乘法与信息流有关,将数据转换为代码并转换回。
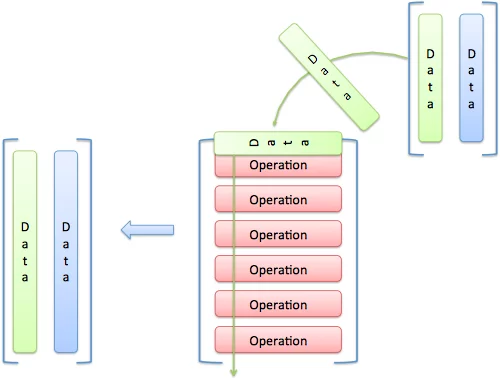
我认为线性代数是“数学电子表格”:
- 我们将信息存储在各种电子表格(“矩阵”)中
- 一些数据被视为要应用的函数,其他数据被视为要使用的数据点
- 我们可以根据需要在向量和函数解释之间切换
有时我会将数据视为几何向量,有时我会将矩阵视为组合函数。但我主要考虑的是系统中的信息流动。
1、开发者的直觉:代码就是数据,数据就是代码
拿你最喜欢的食谱来说吧。如果你把这些词解释为指令,你最终会得到馅饼、松饼、蛋糕等。
如果你把这些词解释为数据,那么文本就是可以调整的散文:
- 将测量单位转换为公制单位
- 由于过敏而更换配料
- 根据海拔高度或不同的设备进行调整
结果是一个新的食谱,可以进一步调整,或作为指令执行,制作不同的馅饼、松饼、蛋糕等。编译器将程序视为文本,对其进行修改,并最终输出“指令”——可能是另一层的文本。
这就是线性代数。我们将“3 4 5”等原始信息视为向量或函数,具体取决于它的写法:
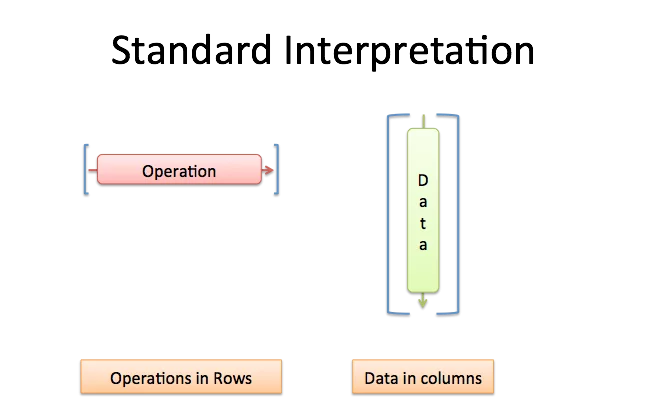
按照惯例,垂直列通常是一个向量,水平行通常是一个函数:
[3; 4; 5]表示x = (3, 4, 5)。这里,x 是一个数据向量(我使用 ; 来分隔每行)。[3 4 5]表示f(a, b, c) = 3a + 4b + 5c。这是一个接受三个输入并返回单个结果的函数。
然后就是顿悟时刻:数据就是代码,代码就是数据!
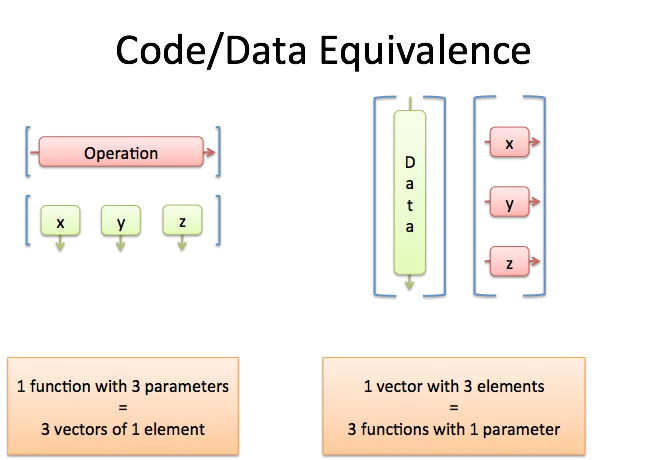
包含水平函数的行实际上可以是三个数据点(每个数据点都有一个元素)。垂直数据列实际上可以是三个不同的函数,每个函数都采用一个参数。
啊。这变得简洁了:根据期望的结果,我们可以以不同的顺序组合数据和代码。
2、矩阵转置
矩阵转置交换行和列。这是它在实践中的含义。
如果 x 是一个有 3 个条目的列向量( [3; 4; 5] ),那么 x' 是:
- 采用 3 个参数的函数(
[3 4 5]) x'仍然可以保留为数据向量,但作为三个单独的条目。转置“将其拆分”。
类似地,如果 f = [3 4 5] 是我们的行向量,那么 f' 可以表示:
- 垂直列中的单个数据向量。
f'分为三个函数(每个函数采用一个输入)。
让我们在实践中使用它。
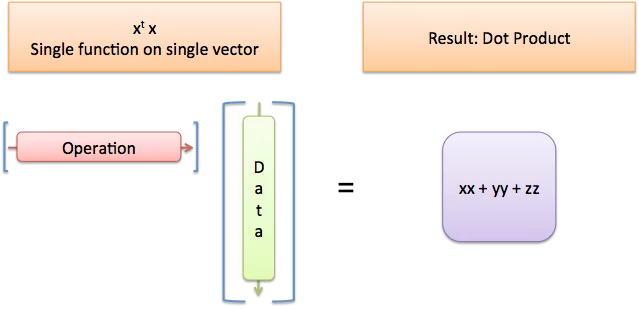
当我们看到 x' * x 时,我们的意思是:`x'`(作为单个函数)正在对 x(单个向量)进行操作。结果是点积。换句话说,我们将数据应用于自身。
当我们看到 x * x' 时,我们的意思是 x(作为一组函数)正在对 x'(一组单独的数据点)进行操作。结果是一个网格,我们将每个函数应用于每个数据点。在这里,我们以每种可能的排列方式将数据与其自身混合在一起。
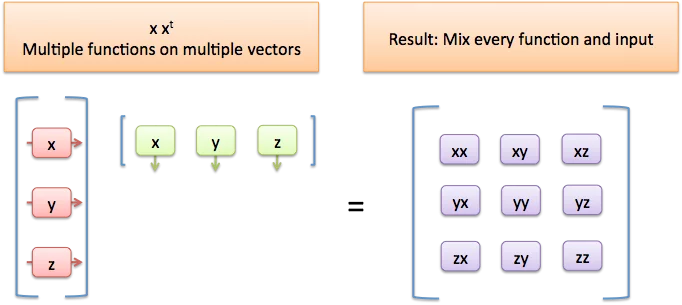
我认为 xx 是 x(x)。它是作用于“向量 x”的“函数 x”。这有助于计算协方差矩阵,即数据中自相似性的度量。
3、将直觉付诸实践
这对我们有什么帮助?当我们看到这样的方程式(来自机器学习课程):
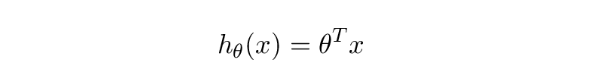
我现在立刻感觉到发生了什么。在第一个方程式中,我们将 θ(通常是一组数据参数)视为一个函数,并将 作为一个参数传入。这应该会给我们一个单一的值。
更复杂的推导如下:
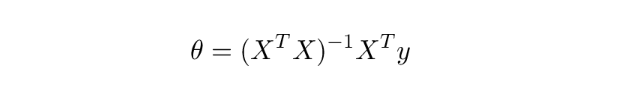
可以同样解读。在某些情况下,这会变得很棘手,因为我们将数据存储为矩阵中的行(而不是列),但现在我有更好的工具可以跟进。你可以开始估计何时会得到一个单一的值,或者何时会得到一个“排列网格”。
几何缩放和线性组合都有它们的位置,但在这里我想考虑信息。“x 中的信息正在成为一个函数,我们将它自己作为参数传递。”
长话短说,不要局限于单一的直觉。乘法从重复加法发展而来,到缩放(小数),到旋转(虚数),到“应用”一个数字到另一个数字(积分),等等。为什么矩阵乘法不一样呢?
原文链接:矩阵乘法的直觉 - BimAnt