【基于 PyTorch 的 Python 深度学习】8 注意力机制（4）：PyTorch 实现（上）

前言

文章性质：学习笔记 📖

学习资料：吴茂贵《 Python 深度学习基于 PyTorch ( 第 2 版 ) 》【ISBN】978-7-111-71880-2

主要内容：根据学习资料撰写的学习笔记，该篇主要介绍了如何使用 PyTorch 实现 Transformer 。

代码链接：Python-DL-PyTorch2/pytorch-08/pytorch-08_01.ipynb

前言

一、使用 PyTorch 实现 Transformer

1、Transformer 背景介绍

2、构建 Encoder-Decorder

3、构建编码器

4、构建解码器

5、构建多头注意力

6、构建前反馈神经网络层

7、预处理输入数据

一、使用 PyTorch 实现 Transformer

Transformer 的原理在前面已经分析得较为详细，本文重点介绍如何使用 PyTorch 来实现。我们将使用 PyTorch 1.0+ 版本完整实现 Transformer 架构，并用简单实例进行验证。本文代码参考了哈佛大学 OpenNMT 团队针对 Transformer 实现的代码。该代码是用 PyTorch 0.3.0 实现的，代码地址为：http://nlp.seas.harvard.edu/2018/04/03/attention.html 。

1、Transformer 背景介绍

目前主流的神经序列转换模型大都基于 Encoder-Decoder 架构。所谓序列转换模型就是把一个输入序列转换成另外一个输出序列，它们的长度可能不同。比如基于神经网络的机器翻译，输入是中文句子，输出是英语句子，这就是一个序列转换模型。类似的，文本摘要、对话等问题都可以看作序列转换问题。虽然这里主要关注机器翻译，但是任何输入是一个序列输出是另外一个序列的问题都可以使用 Encoder-Decoder 模型。

Transformer 使用编码器-解码器模型的架构，只不过它的编码器是由 N(6) 个 EncoderLayer 组成，每个 EncoderLayer 包含一个自注意力 SubLayer 层和一个全连接 SubLayer 层。而它的解码器也是由 N(6) 个 DecoderLayer 组成，每个 DecoderLayer 包含一个自注意力 SubLayer 层、一个注意力 SubLayer 层、一个全连接 SubLayer 层。

编码器 Encoder 把输入序列 ( x1, … , xn ) 映射或编码成一个连续的序列 z = ( z1, … , zn ) 。而解码器 Decoder 根据 z 来解码得到输出序列 y1, … , ym 。解码器 Decoder 是自回归的（Auto-Regressive），会把前一个时刻的输出作为当前时刻的输入。

2、构建 Encoder-Decorder

构建 编码器-解码器模型 的代码如下：

① 导入需要的库。

import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
import math, copy, time

import matplotlib.pyplot as plt
import seaborn
seaborn.set_context(context="talk")

%matplotlib inline

② 构建 Encoder-Decoder 架构。

class EncoderDecoder(nn.Module):
    """
    这是一个标准的 Encoder-Decoder 架构
    """
    def __init__(self, encoder, decoder, src_embed, tgt_embed, generator):
        super(EncoderDecoder, self).__init__()
        # 编码器和解码器都是在构造时传入的，这样会非常灵活
        self.encoder = encoder
        self.decoder = decoder
        # 输入和输出嵌入
        self.src_embed = src_embed  
        self.tgt_embed = tgt_embed 
        # 解码器部分最后的 Linear+softmax
        self.generator = generator  
        
    def forward(self, src, tgt, src_mask, tgt_mask):
        # 接收并处理屏蔽 src 和目标序列，
        # 首先调用 encode 方法对输入进行编码，然后调用 decode 方法进行解码
        return self.decode(self.encode(src, src_mask), src_mask, tgt, tgt_mask)
    
    def encode(self, src, src_mask):
        # 传入参数包括 src 的嵌入和 src_mask
        return self.encoder(self.src_embed(src), src_mask)
    
    def decode(self, memory, src_mask, tgt, tgt_mask):
        # 传入参数包括目标的嵌入，编码器的输出 memory 及两种掩码
        return self.decoder(self.tgt_embed(tgt), memory, src_mask, tgt_mask)

从以上代码可以看出，Encoder 和 Decoder 都使用了 掩码（Mask），即对某些值进行掩盖，使其在参数更新时不产生效果。

Transformer 模型里面涉及两种掩码，分别是 Padding Mask 和 Sequence Mask。

Padding Mask 在所有的 scaled dot-product attention 里都需要用到，而 Sequence Mask 只在 Decoder 的 self-attention 里用到。

（1）Padding Mask

什么是 Padding Mask 呢？因为每个批次输入序列长度是不一样的，也就是说，我们要对输入序列进行对齐。具体来说，如果输入的序列较短，则在后面填充 0 ；如果输入的序列太长，则截取左边的内容，把多余的部分直接舍弃。因为这些填充的位置其实是没什么意义的，所以注意力机制不应该把注意力放在这些位置上，需要进行一些处理。具体的做法是，把这些位置的值加上一个非常大的负数（负无穷），这样经过 softmax ，这些位置的概率就会接近 0 ！而 Padding Mask 实际是一个张量，每个值都是一个布尔值，值为 false 的地方就是我们要进行处理的地方。

（2）Sequence Mask

前文也提到，Sequence Mask 是为了使解码器无法看见未来的信息。也就是说，对于一个序列，在 time_step 为 t 的时刻，解码输出应该只能依赖于 t 时刻之前的输出，而不能依赖 t 之后的输出。因此我们需要想办法把 t 之后的信息给隐藏起来。那么具体怎么做呢？也很简单：生成一个上三角矩阵，上三角的值全为 0 ，然后把这个矩阵作用在每一个序列上。对于解码器的自注意力，里面使用到的缩放的点积注意力 scaled dot-product attention，同时需要 Padding Mask 和 Sequence Mask 作为 attn_mask，具体实现就是两个 Mask 相加作为 attn_mask 。在其他情况下，attn_mask 一律等于 Padding Mask。

③ 创建 Generator 类。通过一个全连接层，再经过 log_softmax 函数的作用，使 Decoder 的输出成为概率值。

class Generator(nn.Module):
    """ 定义标准的一个全连接（linear）+ softmax
    根据解码器的隐状态输出一个词
    d_model 是解码器输出的大小，vocab 是词典大小 """
    def __init__(self, d_model, vocab):
        super(Generator, self).__init__()
        self.proj = nn.Linear(d_model, vocab)
    # 全连接再加上一个 softmax
    def forward(self, x):
        return F.log_softmax(self.proj(x), dim=-1)

3、构建编码器

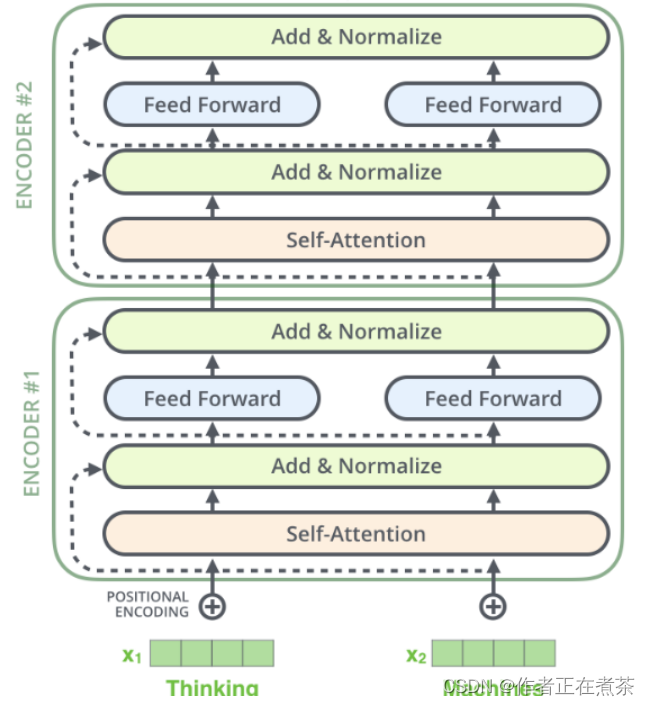
前文提到，编码器 Encoder 是由 N 个相同结构的 Encoderlayer 堆积而成的，而每个 Encoderlayer 层又有两个子层。第一个是多头自注意力层，第二个比较简单，是按位置全连接的前馈网络。其间还有 LayerNorm 及残差连接等。编码器的结构如下图所示。

① 定义复制模块的函数。

首先定义 clones 函数，用于克隆相同的 EncoderLayer 。

def clones(module, N):
    " 克隆 N 个完全相同的 SubLayer，使用了 copy.deepcopy "
    return nn.ModuleList([copy.deepcopy(module) for _ in range(N)])

这里使用了 nn.ModuleList ，ModuleList 就像一个普通的 Python 的 List ，可以使用下标来访问它，其优点是传入的 ModuleList 的所有 Module 都会注册到 PyTorch 中，这样优化器 Optimizer 就能找到其中的参数，从而能够用梯度下降更新这些参数。

但是 nn.ModuleList 并不是 Module（的子类），因此它没有 forward 等方法，我们通常把它放到某个 Module 里。

② 定义编码器 Encoder 。

class Encoder(nn.Module):
    " Encoder 由 N 个 EncoderLayer 堆积而成 "
    def __init__(self, layer, N):
        super(Encoder, self).__init__()
        self.layers = clones(layer, N)
        self.norm = LayerNorm(layer.size)
        
    def forward(self, x, mask):
        " 对输入 (x, mask) 进行逐层处理 "
        for layer in self.layers:
            x = layer(x, mask)
        return self.norm(x) # N 个 EncoderLayer 处理完成之后还需要一个 LayerNorm

编码器就是 N 个 SubLayer 的栈，最后加上一个 LayerNorm 。

③ 定义 LayerNorm 。

class LayerNorm(nn.Module):
    " 构建一个 LayerNorm 模型 "
    def __init__(self, features, eps=1e-6):
        super(LayerNorm, self).__init__()
        self.a_2 = nn.Parameter(torch.ones(features))
        self.b_2 = nn.Parameter(torch.zeros(features))
        self.eps = eps

    def forward(self, x):
        mean = x.mean(-1, keepdim=True)
        std = x.std(-1, keepdim=True)
        return self.a_2 * (x - mean) / (std + self.eps) + self.b_2

论文中的处理过程如下：

x -> x + self-attention(x) -> layernorm(x + self-attention(x)) => y
y -> dense(y) -> y + dense(y) -> layernorm(y + dense(y)) => z（输入下一层）

这里把 layernorm 层放到前面了，即处理过程如下：

x -> layernorm(x) -> self-attention(layernorm(x)) -> x + self-attention(layernorm(x)) => y
y -> layernorm(y) -> dense(layernorm(y)) -> y + dense(layernorm(y)) => z（输入下一层）

PyTorch 中各层权重的数据类型是 nn.Parameter ，而非 Tensor ，需对初始化后的参数（Tensor 型）进行类型转换。每个 Encoder 层又有两个子层，每个子层通过残差把每层的输入输出转换为新的输出。无论是自注意力还是全连接，都首先是 LayerNorm 层，然后是自注意力层 / 稠密层，然后是 dropout 层，最后是残差连接。这里把这个过程封装成 SubLayer Connection。

④ 定义 SublayerConnection 。

class SublayerConnection(nn.Module):
    """
    LayerNorm + SubLayer (Self-Attenion / Dense) + dropout + 残差连接
    为了简单，把 LayerNorm 放到了前面，而原始论文是把 LayerNorm 放在最后
    """
    def __init__(self, size, dropout):
        super(SublayerConnection, self).__init__()
        self.norm = LayerNorm(size)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x, sublayer):
        # 将残差连接应用于具有相同大小的任何子层
        return x + self.dropout(sublayer(self.norm(x)))

⑤ 构建 EncoderLayer 。

class EncoderLayer(nn.Module):
    " Encoder 由 self_attn 和 feed_forward 构成 "
    def __init__(self, size, self_attn, feed_forward, dropout):
        super(EncoderLayer, self).__init__()
        self.self_attn = self_attn
        self.feed_forward = feed_forward
        self.sublayer = clones(SublayerConnection(size, dropout), 2)
        self.size = size

    def forward(self, x, mask):
        " 实现正向传播功能 "
        x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, mask))
        return self.sublayer[1](x, self.feed_forward)

为实现代码的复用，这里把 self_attn 层和 feed_forward 层作为参数传入，只构造两个 SubLayer 。

forward 调用 sublayer[0]（SubLayer 对象），最终会调用其 forward 方法，这个方法需要 2 个参数：输入 Tensor ，对象或函数。

self_attn 函数需要 4 个参数：Query 的输入，Key 的输入，Value 的输入和 Mask 。故使用 lambda 将其变成一个参数 x 的函数。

lambda x: self.self_attn(x, x, x, mask) ，这里可以将 Mask 看作已知数。

4、构建解码器

解码器由 N 个 DecoderLayer 堆积而成，参数 layer 是 DecoderLayer，也是一个调用对象，最终会调用 DecoderLayer.forward 方法，需要 4 个参数：输入 x ，Encoder 的输出 memory ，输入 Encoder 的 Mask(src_mask) ，输入 Decoder 的 Mask(tgt_mask) 。这里所有的 Decoder 的 forward 方法也需要这 4 个参数。解码器的结构如下图所示。

① 定义解码器 Decoder 。

class Decoder(nn.Module):
    " 构建 N 个完全相同的 Decoder 层"
    def __init__(self, layer, N):
        super(Decoder, self).__init__()
        self.layers = clones(layer, N)
        self.norm = LayerNorm(layer.size)
        
    def forward(self, x, memory, src_mask, tgt_mask):
        for layer in self.layers:
            x = layer(x, memory, src_mask, tgt_mask)
        return self.norm(x)

② 定义 DecoderLayer 。

class DecoderLayer(nn.Module):
    " Decoder 包括 self-attn, src-attn 和 feed forward "
    def __init__(self, size, self_attn, src_attn, feed_forward, dropout):
        super(DecoderLayer, self).__init__()
        self.size = size
        self.self_attn = self_attn
        self.src_attn = src_attn
        self.feed_forward = feed_forward
        self.sublayer = clones(SublayerConnection(size, dropout), 3)
 
    def forward(self, x, memory, src_mask, tgt_mask):
        m = memory
        x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, tgt_mask))
        x = self.sublayer[1](x, lambda x: self.src_attn(x, m, m, src_mask))
        return self.sublayer[2](x, self.feed_forward)

DecoderLayer 比 EncoderLayer 多了一个 src-attn 层，这层的输入来自 Encoder 的输出 memory 。

src-attn 和 self-attn 的实现相同，只不过使用的 Query 、Key 和 Value 输入不同。

普通注意力（src-attn）的 Query 由下层输入进来（来自 self-attn 的输出），Key 和 Value 是 Encoder 最后一层的输出 memory 。

自注意力的 Query ，Key 和 Value 都由下层输入进来。

③ 定义 subsequent_mask 函数。

Decoder 和 Encoder 有一个关键的不同：Decoder 在解码第 t 个时刻的时候只能使用 1, … , t 时刻的输入，而不能使用 t+1 时刻及其之后的输入。因此我们需要一个函数来产生一个掩码矩阵，代码如下：

def subsequent_mask(size):
    " Mask out subsequent positions. "
    attn_shape = (1, size, size)
    subsequent_mask = np.triu(np.ones(attn_shape), k=1).astype('uint8')
    return torch.from_numpy(subsequent_mask) == 0

我们看一下这个函数生成的一个简单样例，假设语句长度为 6 。

plt.figure(figsize=(5,5))
plt.imshow(subsequent_mask(6)[0])

运行结果如图 8-44 所示。

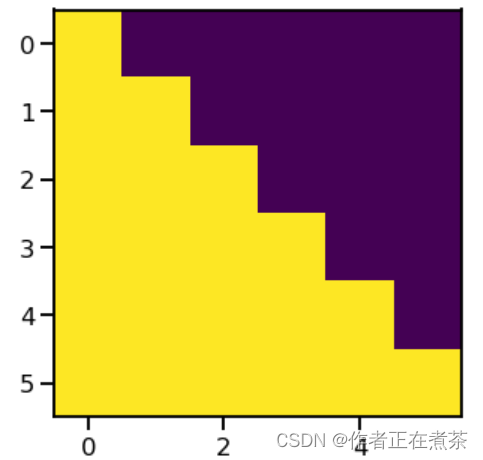
查看序列掩码情况：

subsequent_mask(6)[0]

我们发现它输出的是一个方阵，对角线和下面都是 True 。第一行只有第一列是 True ，它的意思是时刻 1 只能关注输入 1 ，第三行说明时刻 3 可以关注 { 1, 2, 3 } 而不能关注 { 4, 5, 6 } 的输入，因为在真正解码的时候，这是属于预测的信息。知道了这个函数的用途之后，上面的代码就很容易理解了。

5、构建多头注意力

构建多头注意力的过程类似于卷积神经网络中构建多通道的过程，目的都是提升模型的泛化能力。下面来看具体构建过程。

① 定义注意力 attention 。

注意力（包括自注意力和普通的注意力）可以看成一个函数，它的输入是 Query 、Key 、Value 和 Mask，输出是一个 Tensor 。其中输出是 Value 的加权平均，而权重由 Query 和 Key 计算得出。具体的计算公式如下所示：

$Attention(Q,K,V)=Softmax(\frac{QK^T}{\sqrt{d_k}})V$

具体实现代码如下：

def attention(query, key, value, mask=None, dropout=None):
    " 计算缩放的点积注意力 "
    d_k = query.size(-1)
    scores = torch.matmul(query, key.transpose(-2, -1)) / math.sqrt(d_k)
    if mask is not None:
        scores = scores.masked_fill(mask == 0, -1e9)
    p_attn = F.softmax(scores, dim = -1)
    if dropout is not None:
        p_attn = dropout(p_attn)
    return torch.matmul(p_attn, value), p_attn

上面的代码实现 $\frac{QK^T}{\sqrt{d_k}}$ 和公式里稍微不同，这里的 Q 和 K 都是 4 维张量（Tensor），包括 batch 和 head 维度。torch.matmul 会对 Query 和 Key 的最后两维进行矩阵乘法，这样效率更高，如果我们要用标准的矩阵（2 维张量）乘法来实现，那么需要遍历 batch 和 head 两个维度。用一个具体例子跟踪一些不同张量的形状变化，然后对照公式就很容易理解。比如 Q 是 (30, 8, 33, 64) ，其中 30 是 batch 的个数，8 是 head 的个数，33 是序列长度，64 是每个时刻的特征数。K 和 Q 的形状必须相同，而 V 可以不同，但在这里，其形状也是相同的。接下来是 scores.masked_fill(mask == 0, -1e9) ，用于把 mask=0 的得分变成一个很小的数，这样经过softmax 之后的概率就很接近零。self_attention 中的掩码主要是 Padding Mask 格式，与解码器 Decoder 中的掩码格式不同。再对 score 进行 softmax 函数计算，把得分变成概率 p_attn ，如果有 dropout 层，则对 p_attn 进行 dropout（原论文无 dropout 层）。最后把 p_attn 和 value 相乘。p_attn 是 ( 30, 8, 33, 33 ) ，value 是 ( 30, 8, 33, 64 ) ，只看后两堆 (33×33) × (33×64) = (33×64) 。

② 定义多头注意力 Multi-headed Attention 。

前面可视化部分介绍了如何将输入变成 Q 、K 和 V ，对于每一个头都使用 3 个矩阵 $W^Q$ 、 $W^K$ 、 $W^V$ 把输入转换成 Q 、K 和 V 。然后分别用每一个头进行自注意力的计算，把 N 个头的输出拼接起来，与矩阵 $W^Q$ 相乘。具体计算多头注意力的公式如下：

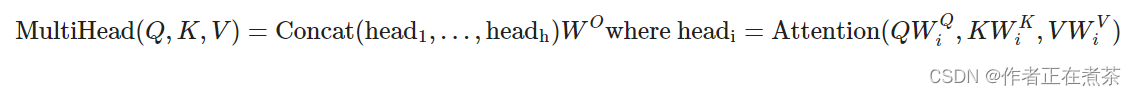
这里的映射是参数矩阵，其中， $h = 8$ ， $d_k=d_v=\frac{d_{model}}{h}=64$ 。

$W_i^Q \in R^{d_{model}d_k} ,W_i^K \in R^{d_{model}d_k},W_i^V \in R^{d_{model}d_v},W_i^O \in R^{hd_vd_{model}}$

详细的计算过程如下：

class MultiHeadedAttention(nn.Module):
    def __init__(self, h, d_model, dropout=0.1):
        " 传入 head 个数及 model 的维度 "
        super(MultiHeadedAttention, self).__init__()
        assert d_model % h == 0
        # 这里假设 d_v = d_k
        self.d_k = d_model // h
        self.h = h
        self.linears = clones(nn.Linear(d_model, d_model), 4)
        self.attn = None
        self.dropout = nn.Dropout(p=dropout)
        
    def forward(self, query, key, value, mask=None):
        " Implements Figure 2 "
        if mask is not None:
            # 相同的 mask 适应所有的 head
            mask = mask.unsqueeze(1)
        nbatches = query.size(0)
        
        # 1) 首先使用线性变换，然后把 d_model 分配给 h 个 head ，每个 head 为 d_k = d_model / h         
        query, key, value = \
            [l(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)
             for l, x in zip(self.linears, (query, key, value))]
        
        # 2) 使用 attention 函数计算 scaled-dot-product-attention 
        x, self.attn = attention(query, key, value, mask=mask, dropout=self.dropout)
        
        # 3) 实现多头注意力，用 view 函数把 8 个 head 的 64 维向量拼接成一个 512 的向量
        # 然后再使用一个线性变换 (512, 521)，shape 不变. 
        x = x.transpose(1, 2).contiguous().view(nbatches, -1, self.h * self.d_k)
        return self.linears[-1](x)

zip(self.linears, (query, key, value)) 是把 (self.linears[0], self.linears[1], self.linears[2]) 和 (query, key, value) 放到一起再进行遍历。

只看 self.linears[0] (query)。根据构造函数的定义，self.linears[0] 是一个 (512, 512) 的矩阵，而 query 是 (batch, time, 512) 。

相乘之后得到新的 query 还是 512 (d_model) 维的向量，接着用 view 把它变成 (batch, time, 8, 64) 。

再调用 transponse 将其变成 (batch, 8, time, 64)，这是 attention 函数要求的 shape。

(batch, 8, time, 64) 分别对应 8 个 head ，每个 head 的 query 都是 64 维。

key 和 value 的运算完全相同，因此也分别得到 8 个 head 的 64 维的 key 和 64 维的 value 。

接着调用 attention 函数，得到 x 和 self.attn 。x 的 shape 是 (batch, 8, time, 64) ，而 attn 是 (batch, 8, time, time) 。

调用 x.transpose(1, 2) 把 x 变成 (batch, time, 8, 64) ，再将其变成 (batch, time, 512) ，即把 8 个 64 维的向量拼接成 512 的向量。

最后用 self.linears[-1] 对 x 进行线性变换，self.linears[-1] 是 (512, 512) ，因此最终的输出还是 (batch, time, 512) 。

最初构造了 4 个 (512, 512) 的矩阵，前 3 个用于对 query ，key 和 value 进行变换，最后一个用于变换 8 个 head 拼接后的向量。

多头注意力的应用：

① Encoder 的 Self-Attention 层：query ，key 和 value 都是相同的值，来自下层的输入。掩码都是 1（当然填充的不算）。

② Decoder 的 Self-Attention 层：query ，key 和 value 都是相同的值，来自下层的输入。但是掩码使得它不能访问未来的输入。

③ Encoder-Decoder 的普通 Attention 层：query 来自下层的输入，而 key 和 value 都是 Encoder 最后一层的输出，掩码都是 1 。

6、构建前反馈神经网络层

除了注意力子层之外，编码器和解码器中的每个层都包含一个完全连接的前馈网络（ Feed Forward ），该网络包括两个线性转换，中间有一个 ReLU 激活函数，具体公式为：

$FFN(x)=max(0,xW_1+b_1)W_2+b_2$

全连接层的输入和输出都是 d_model(512) 维的，中间隐含单元的个数是 d_ff (2048) ，具体代码如下：

class PositionwiseFeedForward(nn.Module):
    " Implements FFN equation "
    def __init__(self, d_model, d_ff, dropout=0.1):
        super(PositionwiseFeedForward, self).__init__()
        self.w_1 = nn.Linear(d_model, d_ff)
        self.w_2 = nn.Linear(d_ff, d_model)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        return self.w_2(self.dropout(F.relu(self.w_1(x))))

7、预处理输入数据

输入的词序列都是 ID 序列，我们需要嵌入 Embedding 。源语言和目标语言都需要 Embedding ，此外我们还需要一个线性变换把隐含变量变成输出概率，这可以通过前面的类 Generator 来实现。Transformer 模型的注意力机制并没有包含位置信息，即一句话中词语在不同的位置时，在 Transformer 中是没有区别的，这当然是不符合实际的。因此，在 Transformer 中引入位置信息相比卷积神经网络 CNN 、循环神经网络 RNN 等模型有更加重要的作用。原论文作者添加位置编码的方法是：构造一个与输入嵌入维度一样的矩阵，然后与输入嵌入相加得到 multi-head attention 的输入。预处理输入数据的过程如图 8-45 所示。

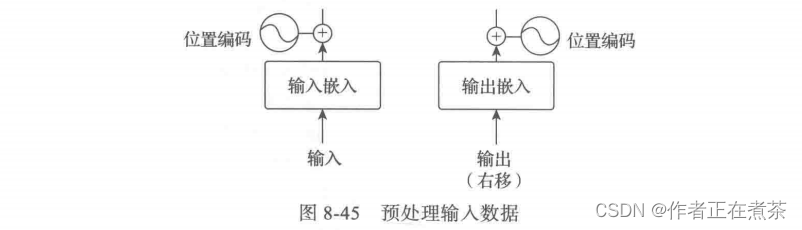
① 先把输入数据转换为输入嵌入，具体代码如下：

class Embeddings(nn.Module):
    def __init__(self, d_model, vocab):
        super(Embeddings, self).__init__()
        self.lut = nn.Embedding(vocab, d_model)
        self.d_model = d_model

    def forward(self, x):
        return self.lut(x) * math.sqrt(self.d_model)

② 添加位置编码。位置编码的公式如下：

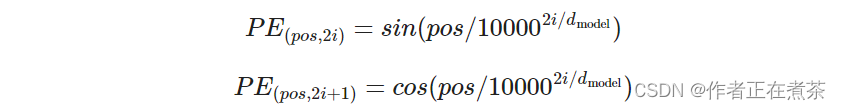
class PositionalEncoding(nn.Module):
    " 实现 PE 函数 "
    def __init__(self, d_model, dropout, max_len=5000):
        super(PositionalEncoding, self).__init__()
        self.dropout = nn.Dropout(p=dropout)
        
        # Compute the positional encodings once in log space.
        pe = torch.zeros(max_len, d_model)
        position = torch.arange(0, max_len).unsqueeze(1)
        div_term = torch.exp(torch.arange(0, d_model, 2) *
                             -(math.log(10000.0) / d_model))
        pe[:, 0::2] = torch.sin(position * div_term)
        pe[:, 1::2] = torch.cos(position * div_term)
        pe = pe.unsqueeze(0)
        self.register_buffer('pe', pe)
        
    def forward(self, x):
        x = x + self.pe[:, :x.size(1)].clone().detach()
        return self.dropout(x)

注意这里调用了 Module.register_buffer 函数。这个函数的作用是创建一个 buffer ，比如把 pi 保存下来。register_buffer 通常用于保存一些模型参数之外的值，比如在 BatchNorm 中，我们需要保存 running_mean(Moving Average) ，它不是模型的参数（不是通过迭代学习的参数），但是模型会修改它，而且在预测的时候也要使用它。这里也是类似的，pe 是一个提前计算好的常量，在构造函数里并没有把 pe 保存到 self 里，但是在 forward 函数中可以直接使用 self.pe 。如果保存（序列化）模型到磁盘，PyTorch 框架将保存 buffer 里的数据到磁盘，这样在反序列化的时候就可以恢复它们。

③ 可视化编码。

假设输入的 ID 序列长度为 10 ，如果输入转为嵌入之后是 (10, 512) ，那么位置编码的输出也是 (10, 512) 。上面公式中的 pos 就是位置 0~9 ，512 维的偶数维使用 sin 函数，而奇数维使用 cos 函数。这种位置编码的好处是：PE 可以表示为 PE+k 式的线性函数，这样网络就能容易地学到相对位置的关系。

图 8-46 是一个示例，向量的大小 d_model=20 ，这里画出第 4 、5 、6 和 7 维的图像（下标从零开始），最大的位置是 100 。

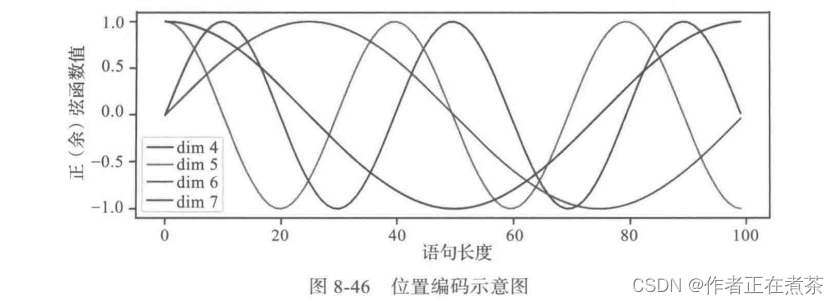
可以看到它们都是正弦（余弦）函数，而且周期越来越长。具体实现代码如下：

## 语句长度为 100 ，这里假设 d_model=20，
plt.figure(figsize=(15, 5))
pe = PositionalEncoding(20, 0)  
y = pe.forward(torch.zeros(1, 100, 20))  
plt.plot(np.arange(100), y[0, :, 4:8].data.numpy())
plt.legend(["dim %d"%p for p in [4,5,6,7]])

④ 下面来看一个生成位置编码的简单示例，代码如下：

d_model, dropout, max_len = 512, 0, 5000
pe = torch.zeros(max_len, d_model)
position = torch.arange(0, max_len).unsqueeze(1)
div_term = torch.exp(torch.arange(0, d_model, 2) * -(math.log(10000.0) / d_model))
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
print(pe.shape)
pe = pe.unsqueeze(0)
print(pe.shape)