C++ | Python气泡表面张力和预期形态及上升速度数值模型

news2024/10/6 23:39:52

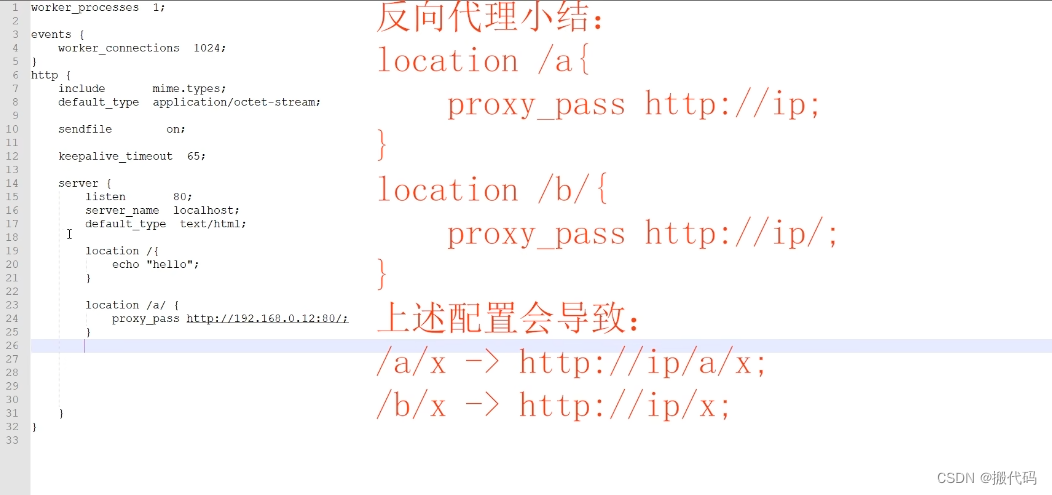
📜模型-用例

📜流体力学：C++风流和MATLAB | Python | CUDA 库埃特流泊肃叶流薄膜流体 | 📜神经网络：Python捕捉重叠气泡单体运动，算法测速
在这里插入图片描述

✒️C++风成和风蚀建模

风成过程是指由风在地表或近地表引起的侵蚀、搬运和沉积物沉积过程。由风作用产生的沉积物以及这些沉积物特有的沉积结构也被描述为风成。风成作用在植被稀少或没有植被的地区最为重要。然而，风成沉积物并不局限于干旱气候。它们也出现在海岸线沿线，半干旱气候的河道沿岸，在由弱胶结砂岩露头风化而成的大量沙子地区以及冰川冲积地区。

风通过风的吹散（风的湍流作用带走松散的细颗粒）和磨蚀（风载颗粒的磨削作用和喷砂作用磨损表面）侵蚀地球表面。一旦被风吹散，颗粒之间的碰撞会进一步分解它们，这一过程称为磨损。在世界范围内，水的侵蚀比风的侵蚀更重要，但风的侵蚀在半干旱和干旱地区很重要。某些人类活动会加剧风蚀，例如使用四轮驱动车辆。

在此，我将使用C++代码解释固体地形上模拟沉积物的方法，包括沉积物的产生和沉积物的运输。我发现风蚀可以通过两个关键效应来描述：吹散、磨蚀。

我的方法是对穿过坚固和松散地形并与之相互作用的“风粒子”进行建模。

风粒子使用特定的运动描述反弹并飞过地形
飞行颗粒与固体地形碰撞会磨损地面，将固体物质转化为松散的沉积物
风粒子在松散的沉积物上移动可以提升一定的量并将其“悬浮”
风粒子飞过空气中的沉积物
每当沉积物被提升或掉落时，附近的松散沉积物就会发生瀑布式沉积物

世界级包含两个有趣的地图：代表坚实地面的高度图和代表分层在顶部的松散颗粒的沉积物图。两张地图都是代表网格（256×256）的简单展平数组：

//...

#define SIZE 256

//...

class World{
public:

  void generate();                      
  void erode(int cycles);                

  //...

  double heightmap[SIZE*SIZE] = {0.0};   
  double sediment[SIZE*SIZE] = {0.0};    

  //...

};

风粒子由三个关键过程描述：

基于风动力学的运动
通过磨损和悬浮进行质量传输
通过级联进行质量沉降

为了捕获这些过程，我们定义了一个风粒子结构：

struct Wind{

  Wind(glm::vec2 _pos){ pos = _pos; }
  Wind(glm::vec2 _p, glm::ivec2 dim){
    pos = _p;
    int index = _p.x*dim.y+_p.y;
  }

  int index;
  glm::vec2 pos;
  float height = 0.0;
  glm::vec3 pspeed = glm::vec3(1.0,0.0,1.0);
  glm::vec3 speed = pspeed;
  double sediment = 0.0; 

  const float dt = 0.25;
  const double suspension = 0.0001;  
  const double abrasion = 0.0001;
  const double roughness = 0.005;
  const double settling = 0.01;

  void fly(double* h, double* path, double* pool, bool* track, glm::ivec2 dim, double scale);
  void cascade(int i, double* height, double* sediment, glm::ivec2 dim);

};

我们定义盛行风速 pspeed，它充当粒子速度的初始条件。风粒子在地形逆风边缘的随机位置产生。fly 函数定义了粒子在其生命周期内的整个运动：

void Wind::fly(double* h, double* w, double* s, bool* track, glm::ivec2 dim, double scale){
  glm::ivec2 ipos;
  while(true){

    ipos = pos;                    
    int ind = ipos.x*dim.y+ipos.y; 
    if(height < h[ind] + s[ind]) height = h[ind] + s[ind];
    glm::vec3 n = surfaceNormal(pos, h, s, dim, scale);

    //...

如果粒子在表面上滑动或碰撞，它就会发生偏转。我们使用以下方式描述偏转方向：
$\underline{a}=(\underline{n} \times(\underline{n} \times \underline{v}))=(\underline{n} \times \underline{h})$
其中 $n$ 是偏转点处的表面法线， $v$ 是粒子的速度。矢量 a 表示表面法线 $n$ 的法线矢量，它与速度矢量 $v$ 和表面法线 $n$ 位于同一平面。偏转角度的这种表达式具有额外的效果，即向下移动并与表面碰撞的粒子将通过沿着下降路径偏转而正确地沿着表面移动。

对于在空气中飞行的粒子，我们假设它没有受到阻力并继续其飞行路径，同时在重力作用下缓慢向下加速。结合退出地图或变得静止时的中断条件，我们实现了完整的运动：

 //...

    if(height > h[ind] + s[ind]){  
      speed.y -= dt*0.01; 
    }
    else{                        
      track[ind] = true;           
      speed += dt*glm::cross(glm::cross(speed,n),n);
    }

    speed += 0.1f*dt*(pspeed - speed);
    pos += dt*glm::vec2(speed.x, speed.z);
    height += dt*speed.y;
    int nind = (int)pos.x*dim.y+(int)pos.y;
    if(!glm::all(glm::greaterThanEqual(pos, glm::vec2(0))) ||
       !glm::all(glm::lessThan((glm::ivec2)pos, dim)))
         break;

    if(length(speed) < 0.01)
      break;

  }
};