1.两两交换链表中的节点
24. 两两交换链表中的节点 - 力扣(LeetCode)
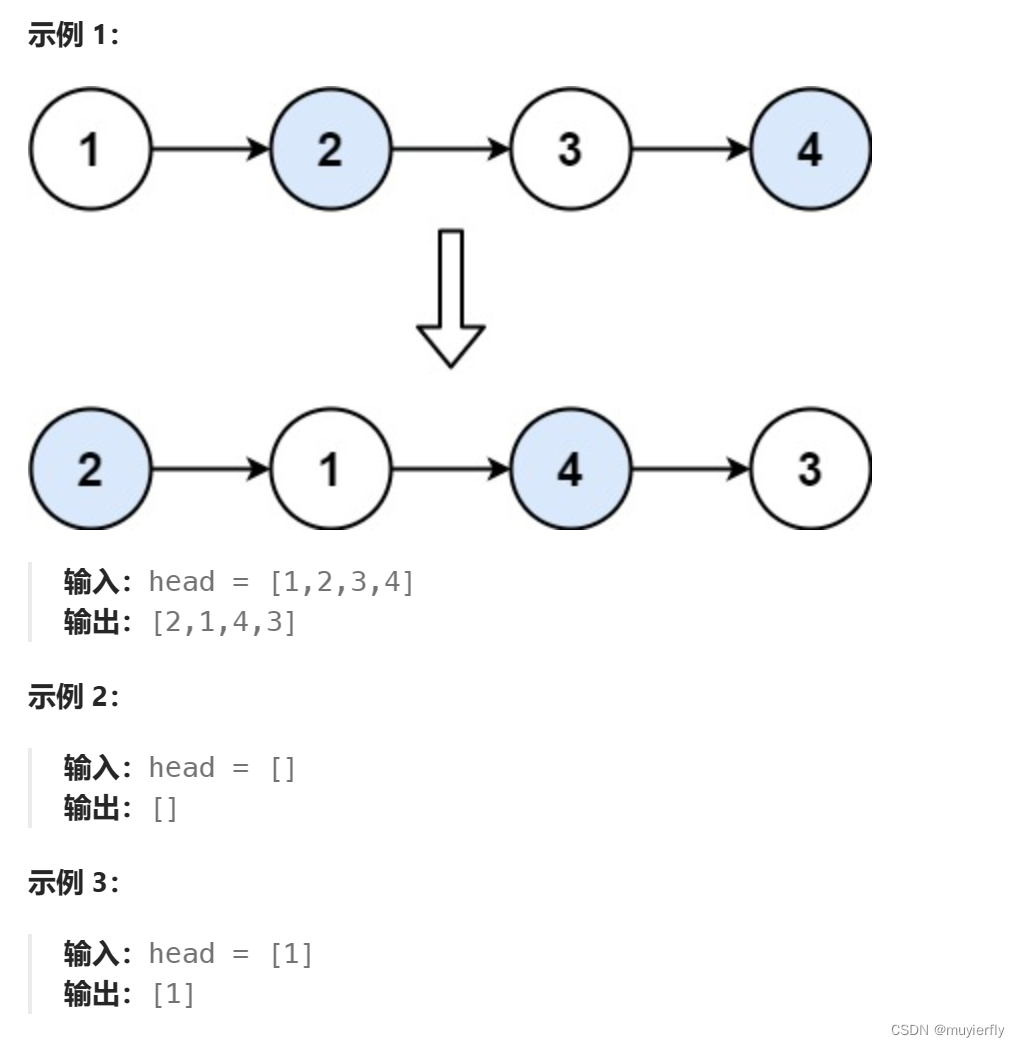
给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
方法一:递归(不好想)
可以通过递归的方式实现两两交换链表中的节点。
递归的终止条件是链表中没有节点,或者链表中只有一个节点,此时无法进行交换。
如果链表中至少有两个节点,则在两两交换链表中的节点之后,原始链表的头节点变成新的链表的第二个节点,原始链表的第二个节点变成新的链表的头节点。
链表中的其余节点的两两交换可以递归地实现。在对链表中的其余节点递归地两两交换之后,更新节点之间的指针关系,即可完成整个链表的两两交换。
class Solution {
public ListNode swapPairs(ListNode head) {
//递归完成的标志
if(head==null||head.next==null){
return head;
}
//假如有两个节点a,b
ListNode newHead=head;
head.next=swapPairs(newHead.next);
newHead.next=head;
return newHead;
}
}方法二:迭代
也可以通过迭代的方式实现两两交换链表中的节点。
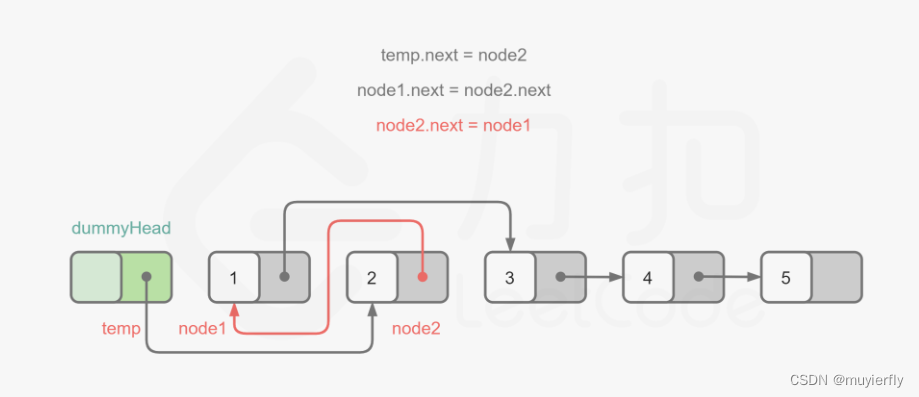
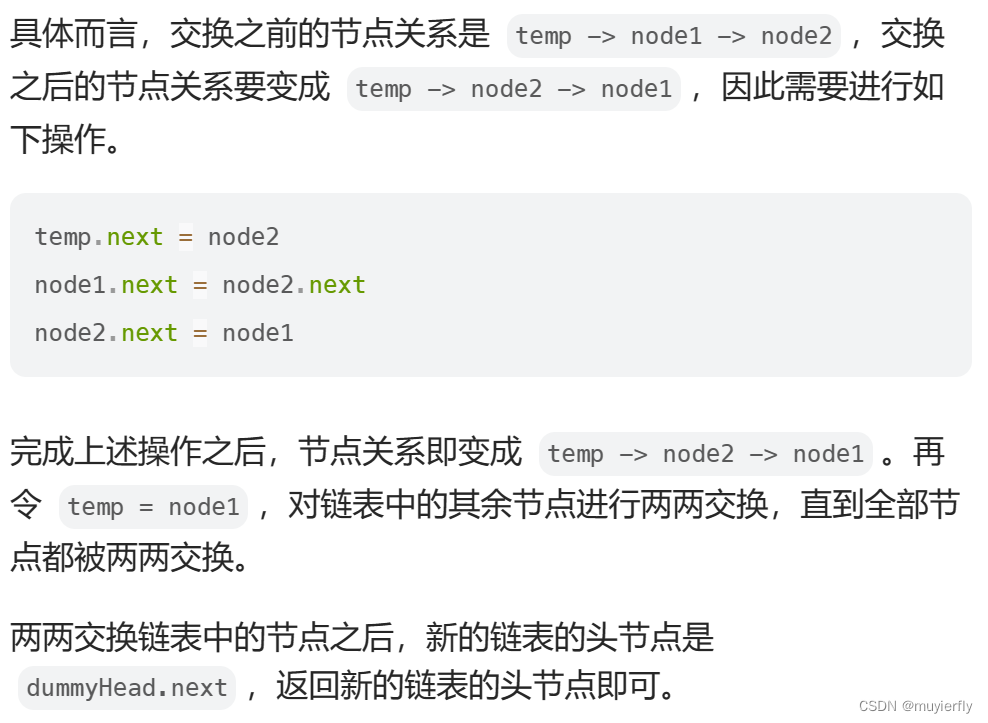
创建哑结点 dummyHead,令 dummyHead.next = head。令 temp 表示当前到达的节点,初始时 temp = dummyHead。每次需要交换 temp 后面的两个节点。
如果 temp 的后面没有节点或者只有一个节点,则没有更多的节点需要交换,因此结束交换。否则,获得 temp 后面的两个节点 node1 和 node2,通过更新节点的指针关系实现两两交换节点。
class Solution {
public ListNode swapPairs(ListNode head) {
//创建哑结点 dummyHead
//先把哑结点添加到链表中
ListNode dummyHead = new ListNode(0);
dummyHead.next=head;
ListNode temp=dummyHead;
while(temp.next!=null&&temp.next.next!=null){
ListNode node1=temp.next;
ListNode node2=temp.next.next;
temp.next=node2;
node1.next=node2.next;
node2.next=node1;
temp=node1;
}
return dummyHead.next;
}
}2.删除有序数组的重复项
26. 删除有序数组中的重复项 - 力扣(LeetCode)
给你一个 非严格递增排列 的数组
nums,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回nums中唯一元素的个数。考虑
nums的唯一元素的数量为k,你需要做以下事情确保你的题解可以被通过:
- 更改数组
nums,使nums的前k个元素包含唯一元素,并按照它们最初在nums中出现的顺序排列。nums的其余元素与nums的大小不重要。- 返回
k。
class Solution {
public int removeDuplicates(int[] nums) {
if(nums == null || nums.length == 0){
return 0;
}
int i=0;
int j=1;
while(j<nums.length){
if(nums[i] == nums[j]){
j++;
}else{
i++;
nums[i]=nums[j];
j++;
}
}
return i+1;
}
}3.移除元素
27. 移除元素 - 力扣(LeetCode)
给你一个数组
nums和一个值val,你需要 原地 移除所有数值等于val的元素。元素的顺序可能发生改变。然后返回nums中与val不同的元素的数量。假设
nums中不等于val的元素数量为k,要通过此题,您需要执行以下操作:
- 更改
nums数组,使nums的前k个元素包含不等于val的元素。nums的其余元素和nums的大小并不重要。- 返回
k。
class Solution {
public int removeElement(int[] nums, int val) {
int left=0;
int right=nums.length;
int count=0;
while(left<right){
if(nums[left]==val){
nums[left]=nums[right-1];
right--;
}else{
left++;
count++;
}
}
return count;
}
}4.找出字符串第一个匹配的下标(重点)
28. 找出字符串中第一个匹配项的下标 - 力扣(LeetCode)
class Solution {
public static int strStr(String haystack, String needle) {
int count=needle.length();
for(int i=0;i<haystack.length()-count+1;i++){
System.out.println(haystack.substring(i,i+count));
if(haystack.substring(i,i+count).equals(needle)){
return i;
}
}
return -1;
}
}
但我们可以看出此时所费的时间很长
考虑另一种经典的算法
方法一:Knuth-Morris-Pratt 算法(经典的字符串匹配)
快速的从主串中找到相同串
KMP算法-超细超全讲解(上)原理篇_哔哩哔哩_bilibili(详细)
class Solution {
public int strStr(String haystack, String needle) {
int n = haystack.length(), m = needle.length();
if (m == 0) {
return 0;
}
int[] pi = new int[m];
for (int i = 1, j = 0; i < m; i++) {
while (j > 0 && needle.charAt(i) != needle.charAt(j)) {
j = pi[j - 1];
}
if (needle.charAt(i) == needle.charAt(j)) {
j++;
}
pi[i] = j;
}
for (int i = 0, j = 0; i < n; i++) {
while (j > 0 && haystack.charAt(i) != needle.charAt(j)) {
j = pi[j - 1];
}
if (haystack.charAt(i) == needle.charAt(j)) {
j++;
}
if (j == m) {
return i - m + 1;
}
}
return -1;
}
}
5.两数相除(重点)
29. 两数相除 - 力扣(LeetCode)
方法一:二分法
不用除法求解中位数的方法
class Solution {
public int divide(int dividend, int divisor) {
//考虑被除数作为最小值的情况
if(dividend==Integer.MIN_VALUE){
//divisor为除数
if(divisor==1){
return Integer.MIN_VALUE;
}
if(divisor==-1){
return Integer.MAX_VALUE;
}
}
//考虑除数为最小值(此时绝对值最大)的情况
if(divisor==Integer.MIN_VALUE){
return dividend==divisor?1:0;
}
//考虑被除数为0的情况
//被除数➗除数
if(dividend==0){
return 0;
}
//上面是特殊情况
//后续我们只需要考虑一般情况
//一般情况,使用二分查找
//将所有的正数取相反数,这样就只用考虑一种情况
boolean rev=false;
if(dividend>0){
dividend=-dividend;
rev=!rev;
}
if(divisor>0){
divisor=-divisor;
rev=!rev;
}
int left=1,right=Integer.MAX_VALUE,ans=0;
while(left<=right){
//注意溢出
//不能使用除法
int mid=left+(right-left)>>1;
boolean check=quickAdd(divisor,mid,dividend);
if(check){
ans=mid;
//注意溢出
if(mid==Integer.MAX_VALUE){
break;
}
left=mid+1;
}else{
right=mid-1;
}
}
return rev?-ans:ans;
//rev本身是false
//如果没改变,就证明原先就是俩负数,所得的结果是大于0
//改变任意一个,结果都是负数,即true的时候,结果为-ans
}
//上述特殊情况
//X和Y都是负数
//根据除法以及余数的定义
//1.我们首先直到暴力求解
//X/Y可以进行分解
//X-Y>Y,COUNT++
//直到X-Y<Y时才证明除完了
//我们将上述思想改成乘法的等价形式
//Z*Y>=X>(Z+1)*Y
//因此我们可以使用二分法得到Z,找出最大的Z使得上述不等式成立
//快速乘
public boolean quickAdd(int y,int z,int x){
//x和y是负数,z是正数
//被除数X➗除数Y
//Z*X>=X是否成立
int result=0,add=y;//y是除数
while(z!=0){
if((z&1)!=0){
//需要保证result+add>=x
//result<x-add意味着我们后续要把left,mid,right的范围画在原先的后部分
//0<10-5
//这就意味着前部分是不行的
if(result<x-add){
return false;
}
result=result+add;
}
if(z!=1){
//需要保证add+add>=x
if(add<x-add){
return false;
}
add+=add;
}
//不能使用除法
//二分法,求z的中间值
z=z>>1;
}
return true;
//true的时候,我们所对应的范围是原来范围的前部分
}
}方法二:类二分法
class Solution {
public int divide(int dividend, int divisor) {
// 考虑被除数为最小值的情况
if (dividend == Integer.MIN_VALUE) {
if (divisor == 1) {
return Integer.MIN_VALUE;
}
if (divisor == -1) {
return Integer.MAX_VALUE;
}
}
// 考虑除数为最小值的情况
if (divisor == Integer.MIN_VALUE) {
return dividend == Integer.MIN_VALUE ? 1 : 0;
}
// 考虑被除数为 0 的情况
if (dividend == 0) {
return 0;
}
// 一般情况,使用类二分查找
// 将所有的正数取相反数,这样就只需要考虑一种情况
boolean rev = false;
if (dividend > 0) {
dividend = -dividend;
rev = !rev;
}
if (divisor > 0) {
divisor = -divisor;
rev = !rev;
}
List<Integer> candidates = new ArrayList<Integer>();
candidates.add(divisor);
int index = 0;
// 注意溢出
while (candidates.get(index) >= dividend - candidates.get(index)) {
candidates.add(candidates.get(index) + candidates.get(index));
++index;
}
int ans = 0;
for (int i = candidates.size() - 1; i >= 0; --i) {
if (candidates.get(i) >= dividend) {
ans += 1 << i;
dividend -= candidates.get(i);
}
}
return rev ? -ans : ans;
}
}