HDU - 5651 xiaoxin juju needs help（Java JS Python C C++）

news2024/11/25 0:26:23

题目来源

Problem - 5651 (hdu.edu.cn)

题目描述

众所周知，小新是一位才华横溢的程序员。当他还是小学六年级的学生时，他就知道回文字符串了。

今年夏天，他在腾讯实习。一天，他的领导来找小新帮忙。他的领导给了他一个字符串，他想让小新为他生成回文字符串。

一旦小新生成一个不同的回文串，他的领导就会给他一个西瓜糖。

问：小新的领导需要买多少糖果?

输入描述

这个问题有多个测试用例。

第一行，包含单个整数 T，它表示测试用例的数量。

  • T ≤ 20

对于每个测试用例，有一行，包含字符串S。

  • 1 ≤ length(S) ≤ 1000

输出描述

对于每个测试用例，打印一个整数，这是小新的领导需要购买的西瓜糖的数量，模取1,000,000,007。

用例

输入3
aa
aabb
a
输出1
2
1

题目解析

本题的解题思路其实很简单。

给定一个字符串s，我们可以任意重排s内字符的顺序，如果新串是回文串，则结果数量+1。

比如：s = "aabb"，重排后有："baab"，"abba" 两种回文串。

那么，我们该如何求解一个字符串重排后可得的回文串数量呢？

思路很简单：

首先，我们需要统计字符串s中各个字符的出现次数

然后，检查“出现次数为奇数次”的字符的数量，如果这个数量超过1，那么字符串s就无法重排出回文串，因为回文串是左右对称的，即可以在中间位置一分为二，比如：

  • 没有“出现次数为奇数次”的字符

  • 有一个“出现次数为奇数次”的字符


  • 但是如果有一个以上的“出现次数为奇数次”的字符时，某一边就会多出无法对称的字符

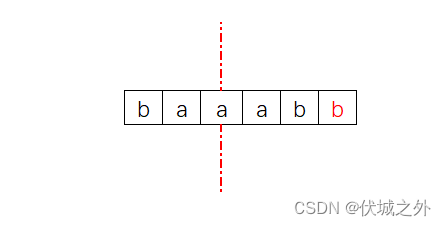
因此，如果统计到的“出现次数为奇数次”的字符数量＞1，则对应字符串s无法重排出回文串。

反之，如果统计到的“出现次数为奇数次”的字符数量 ≤ 1，则对应字符串s可以重排出回文串。但是如果计算可以重排的回文串数量呢？

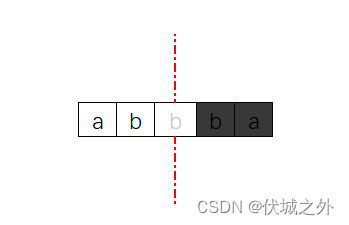
比如s = "aabb"，那么有如下两种情况：

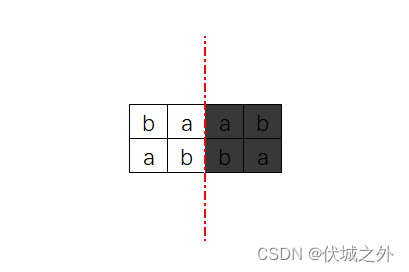
由于回文串是左右对称的，因此，当我们求出回文串的左半部分时，其右半部分也自然确定了。

比如，回文串左半部分是"ab"，那么回文串右半部分必然是"ba"。

因此，我们可以将之前统计的字符串s的各个字符数量除以2，得到回文串左半部分的各字符数量，然后求回文串左半部分的（不重复的）全排列数量，即为回文串的数量。

比如 s = "aabb"，其中统计结果 a字符有2个，b字符有2个，

那么用于组成回文串左半部分的字符数量为：a字符1个，b字符1个。

而1个a字符，一个b字符，可以组成的全排列有"ab"和"ba"两种。即对应的回文串有2种。

另外，还有一个需要注意的是，如果s = "abbba"，其中统计结果：a字符有2个，b字符有3个

那么用于组成回文串左半部分的字符数量为：a字符1个，b字符1.5个？

其实，此时“出现奇数次”的b字符，可以抠出来一个b固定为回文串的中间字符，这个作为中间字符的b既不属于左半部分，也不属于右半部分。

因此，我们可以理解为：回文串左半部分字符数量为：a字符1个，b字符1个（即：3整除2的结果）

那么本题的问题又可以变为：求一组元素的不重复的全排列数量。

假设有n个数，则这n个数的全排列数量即为：n!

比如 [1,2,3] 的全排列有 3！个，分别为：

  • 123
  • 132
  • 213
  • 231
  • 312
  • 321

那么这n个数如果存在重复元素，比如 [1,2,2] 的全排列有：

  • 122
  • 122
  • 212
  • 221
  • 212
  • 221

其中画删除线的都是重复的全排列，那么此时该如何求解不重复的全排列数量呢？

假设有 n 个字符，分为 k 种，

第1种有n1个相同字符，第2种有n2个相同字符，...，第k种有nk个相同字符，

存在关系：n1+n2+...+nk == n

那么，此时不重复全排列数量为：

n! / n1! / n2! / ... / nk! 

比如 [1,2,2] 的有两种字符：字符1有1个，字符2有2个，那么其不重复的全排列数量为：

3! / 1! / 2!

以上就是本题的基础解题思路，总结一下就是：

  • 首先，统计字符串s中各个字符的出现次数
  • 然后，检查“出现次数为奇数次”的字符的数量，如果这个数量超过1，则字符串s无法重排出回文串，即结果为0，否则继续下一步
  • 之后，将各个字符数量整除2，得到回文串左半部分各字符数量
  • 最后，基于回文串左半部分各字符数量求不重复的全排列数量，即为字符串s可以重排出的回文串数量

题目输出描述中说：需要对输出结果值取模1,000,000,007。因此本题的结果实际为：

（n! / n1! / n2! / ... / nk! ）% 1000000007

但是，这里面有一个问题，那就是，字符串s长度最大1000，也就是说回文串左半部分字符总数最大可以n=500，因此按照上面策略，我们必然要求解 500!，这是一个极其庞大的数，计算过程中肯定会long溢出。

当然，如果你的编程语言支持大数的四则运算的话，可以不用担心这个问题，比如Java的BigInteger类型，JS的BigInt类型。

但是其他语言，比如C/C++语言不支持大数的四则运算，Python不支持大数除法（可以支持大数的加法、减法，乘法）。

因此我们依旧需要考虑如果避免整型溢出。

这题为什么要我们将结果值对1000000007，即1e9 + 7取模呢？

因为这涉及到一个知识点：除法取模

算法竞赛6.1-模运算_哔哩哔哩_bilibili

而除法取模又涉及到了：乘法逆元

【C++/算法】乘法逆元详解_哔哩哔哩_bilibili

而乘法逆元的求解又涉及到了：费马小定理

数论：费马小定理_哔哩哔哩_bilibili

由费马小定理公式，类比为，乘法逆元公式，我们又需要基于：快速幂算法来求解逆元

【C++/算法】快速幂算法详解_哔哩哔哩_bilibili

Java算法源码

解法一：基于BigInteger类型
import java.math.BigInteger;
import java.util.Scanner;

public class Main {
    static BigInteger[] fact = new BigInteger[501];

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        // 初始化1~500的阶乘
        initFact();

        // 输入获取
        int t = Integer.parseInt(sc.nextLine());
        for (int i = 0; i < t; i++) {
            String s = sc.nextLine();
            // 核心代码调用
            System.out.println(solution(s));
        }
    }

    public static void initFact() {
        fact[0] = new BigInteger("1");

        for (int i = 1; i <= 500; i++) {
            fact[i] = new BigInteger(i + "").multiply(fact[i - 1]);
        }
    }

    public static String solution(String s) {
        // 求s串每个字符c的数量
        int[] count = new int[26];
        for (int i = 0; i < s.length(); i++) {
            char c = s.charAt(i);
            count[c - 'a']++;
        }

        // "出现次数为奇数次的"字符的数量
        int odd = 0;
        for (int i = 0; i < 26; i++) {
            if (count[i] % 2 != 0) {
                odd++;
            }

            count[i] /= 2; // 只保留一半字符数量, 后续只需要用到回文串的左半部分，即一半的字符
        }

        // 如果"出现次数为奇数次的"字符的数量不止1个，则s串无法重组出回文串
        if (odd > 1) {
            return "0";
        }

        // 不重复的全排列数
        BigInteger ans = fact[s.length() / 2];
        for (int i = 0; i < 26; i++) {
            ans = ans.divide(fact[count[i]]);
        }

        return ans.mod(new BigInteger("1000000007")).toString();
    }
}
解法二：除法取模，乘法逆元，费马小定理，快速幂
import java.util.Scanner;

public class Main {
    static final long mod = 1000000007;
    static long[] fact = new long[501];

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        // 初始化1~500的阶乘
        initFact();

        // 输入获取
        int t = Integer.parseInt(sc.nextLine());
        for (int i = 0; i < t; i++) {
            String s = sc.nextLine();
            // 核心代码调用
            System.out.println(solution(s));
        }
    }

    public static void initFact() {
        fact[0] = 1;

        for (int i = 1; i <= 500; i++) {
            fact[i] = i * fact[i - 1] % mod;
        }
    }

    public static long solution(String s) {
        // 求s串每个字符c的数量
        int[] count = new int[26];
        for (int i = 0; i < s.length(); i++) {
            char c = s.charAt(i);
            count[c - 'a']++;
        }

        // "出现次数为奇数次的"字符的数量
        int odd = 0;
        for (int i = 0; i < 26; i++) {
            if (count[i] % 2 != 0) {
                odd++;
            }

            count[i] /= 2; // 只保留一半字符数量, 后续只需要用到回文串的左半部分，即一半的字符即可
        }

        // 如果"出现次数为奇数次的"字符的数量不止1个，则s串无法重组出回文串
        if (odd > 1) {
            return 0;
        }

        // 不重复的全排列数
        long ans = fact[s.length() / 2];
        for (int i = 0; i < 26; i++) {
            // 假设 x == fact[count[i] / 2]
            // ans / x % mod
            // 等价于
            // ans * x的乘法逆元 % mod
            // 而x的乘法逆元为 fast_pow(x, mod-2, mod)
            ans = ans * fast_pow(fact[count[i]], mod - 2, mod) % mod;
        }

        return ans;
    }

    // 快速幂算法：用于求解 (a^b) % mod 的结果
    public static long fast_pow(long a, long b, long mod) {
        long ans = 1; // 记录结果

        a %= mod;

        // 快速幂算法是为了高效计算a^b, 举例
        // 3^5
        //  = 3 * 3^4
        //  = 3 * 9^2
        //  = 3 * 81^1
        //  = 3 * 81 * 81^0
        // 这个过程中如果发现b为奇数，则析出一个底a作为乘数, 实现 b-=1
        // 这个过程中如果发现b为偶数，则底a进行平方运算，实现 b/=2
        // 这个算法求解a^b的时间复杂度为O(log2(b)), 相较于O(b)算法十分高效
        while (b != 0) {
            if (b % 2 == 1) { // 位运算优化： if(b&1 == 1)
                // 3^5 析出来一个3后, 变为 3 * 3^4, 将b值从奇数变为偶数
                // 下面将析出的来3合入结果ans中, 则剩余3^4
                ans = (ans * a) % mod;
                // b -= 1; // 可以不用此步, 因为后面b会整除2
            }

            // 3^4 变为 9^2
            a = (a * a) % mod; // 底数3 变为 9
            b /= 2; // 幂4 变为 2  // 位运算优化： b>>=1
        }

        return ans;
    }
}

JS算法源码

解法一：基于BigInt类型
const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;

let fact;

void (async function () {
  // 初始化1~500的阶乘
  initFact();

  // 输入获取
  const t = parseInt(await readline());
  for (let i = 0; i < t; i++) {
    const s = await readline();
    // 核心代码调用
    console.log(solution(s));
  }
})();

function initFact() {
  fact = new Array(501);

  fact[0] = BigInt(1);
  for (let i = 1; i <= 500; i++) {
    fact[i] = BigInt(i) * fact[i - 1];
  }
}

function solution(s) {
  // 求s串每个字符c的数量
  const count = new Array(26).fill(0);
  for (let i = 0; i < s.length; i++) {
    count[s.charCodeAt(i) - 97]++;
  }

  // "出现次数为奇数次的"字符的数量
  let odd = 0;
  for (let i = 0; i < 26; i++) {
    if (count[i] % 2 != 0) {
      odd++;
    }

    count[i] = parseInt(count[i] / 2); // 只保留一半字符数量, 后续只需要用到回文串的左半部分，即一半的字符
  }

  // 如果"出现次数为奇数次的"字符的数量不止1个，则s串无法重组出回文串
  if (odd > 1) {
    return "0";
  }

  // 不重复的全排列数
  let ans = fact[parseInt(s.length / 2)];
  for (let i = 0; i < 26; i++) {
    ans = ans / fact[count[i]];
  }

  return (ans % BigInt("1000000007")).toString();
}
解法二：除法取模，乘法逆元，费马小定理，快速幂

JS使用快速幂的意义不大，因为JS普通数值最大只能表示(2^53)-1，如果超出这个数值，那么计算结果就会不准确。

而求解快速幂的过程中，是非常有可能产生一个大于(2^53)-1的值的，JS貌似没有像Java一样做long * long % long 这种计算过程的精度保护。

因此，JS实现快速幂的过程中，我们还是需要使用BigInt，那么又有什么意义使用快速幂呢？

const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;

const mod = BigInt(1000000007);
const fact = new Array(501);

void (async function () {
  // 初始化1~500的阶乘
  initFact();

  // 输入获取
  const t = parseInt(await readline());
  for (let i = 0; i < t; i++) {
    const s = await readline();
    // 核心代码调用
    console.log(solution(s));
  }
})();

function initFact() {
  fact[0] = 1n;
  for (let i = 1; i <= 500; i++) {
    fact[i] = (BigInt(i) * fact[i - 1]) % mod;
  }
}

function solution(s) {
  // 求s串每个字符c的数量
  const count = new Array(26).fill(0);
  for (let i = 0; i < s.length; i++) {
    count[s.charCodeAt(i) - 97]++;
  }

  // "出现次数为奇数次的"字符的数量
  let odd = 0;
  for (let i = 0; i < 26; i++) {
    if (count[i] % 2 != 0) {
      odd++;
    }

    count[i] >>= 1; // 只保留一半字符数量, 后续只需要用到回文串的左半部分，即一半的字符
  }

  // 如果"出现次数为奇数次的"字符的数量不止1个，则s串无法重组出回文串
  if (odd > 1) {
    return 0;
  }

  // 不重复的全排列数
  let ans = fact[s.length >> 1];
  for (let i = 0; i < 26; i++) {
    // 假设 x == fact[count[i] / 2]
    // ans / x % mod
    // 等价于
    // ans * x的乘法逆元 % mod
    // 而x的乘法逆元为 fast_pow(x, mod-2, mod)
    ans = (ans * fast_pow(fact[count[i]], mod - 2n, mod)) % mod;
  }

  return ans.toString();
}

// 快速幂算法：用于求解 (a^b) % mod 的结果
function fast_pow(a, b, mod) {
  let ans = 1n; // 记录结果

  a %= mod;

  // 快速幂算法是为了高效计算a^b, 举例
  // 3^5
  //  = 3 * 3^4
  //  = 3 * 9^2
  //  = 3 * 81^1
  //  = 3 * 81 * 81^0
  // 这个过程中如果发现b为奇数，则析出一个底a作为乘数, 实现 b-=1
  // 这个过程中如果发现b为偶数，则底a进行平方运算，实现 b/=2
  // 这个算法求解a^b的时间复杂度为O(log2(b)), 相较于O(b)算法十分高效
  while (b != 0n) {
    if (b % 2n == 1n) {
      // 3^5 析出来一个3后, 变为 3 * 3^4, 将b值从奇数变为偶数
      // 下面将析出的来3合入结果ans中, 则剩余3^4
      ans = (ans * a) % mod;
      b -= 1n;
    }

    // 3^4 变为 9^2
    a = (a * a) % mod; // 底数3 变为 9
    b /= 2n; // 幂4 变为 2
  }

  return ans;
}

Python算法源码

解法一：除法取模，乘法逆元，费马小定理，快速幂
# 全局变量
fact = [0] * 501
mod = 1000000007


def initFact():
    fact[0] = 1
    for i in range(1, 501):
        fact[i] = i * fact[i - 1] % mod


# 快速幂算法：用于求解 (a^b) % mod 的结果
def fast_pow(a, b):
    ans = 1  # 记录结果

    a %= mod

    # 快速幂算法是为了高效计算a^b, 举例
    # 3 ^ 5
    # = 3 * 3 ^ 4
    # = 3 * 9 ^ 2
    # = 3 * 81 ^ 1
    # = 3 * 81 * 81 ^ 0
    # 这个过程中如果发现b为奇数，则析出一个底a作为乘数, 实现 b -= 1
    # 这个过程中如果发现b为偶数，则底a进行平方运算，实现 b /= 2
    # 这个算法求解a ^ b的时间复杂度为O(log2(b)), 相较于O(b)算法十分高效
    while b != 0:
        if b % 2 == 1:  # 位运算优化： if(b&1 == 1)
            # 3^5 析出来一个3后, 变为 3 * 3^4, 将b值从奇数变为偶数
            # 下面将析出的来3合入结果ans中, 则剩余3^4
            ans = ans * a % mod
            # b -= 1; # 可以不用此步, 因为后面b会整除2

        # 3^4 变为 9^2
        a = a * a % mod  # 底数3 变为 9
        b //= 2  # 幂4 变为 2  # 位运算优化： b>>=1

    return ans


def solution(s):
    # 求s串每个字符c的数量
    count = [0] * 26
    for i in range(len(s)):
        count[ord(s[i]) - 97] += 1

    # "出现次数为奇数次的"字符的数量
    odd = 0
    for i in range(26):
        if count[i] % 2 != 0:
            odd += 1

        count[i] //= 2  # 只保留一半字符数量, 后续只需要用到回文串的左半部分，即一半的字符即可

    # 如果"出现次数为奇数次的"字符的数量不止1个，则s串无法重组出回文串
    if odd > 1:
        return 0

    # 不重复的全排列数
    ans = fact[len(s) // 2]
    for i in range(26):
        # 假设 x == fact[count[i] / 2]
        # ans / x % mod
        # 等价于
        # ans * x的乘法逆元 % mod
        # 而x的乘法逆元为 fast_pow(x, mod-2, mod)
        ans = ans * fast_pow(fact[count[i]], mod - 2) % mod

    return ans


if __name__ == '__main__':
    # 初始化1~500的阶乘
    initFact()

    # 输入获取
    t = int(input())
    for _ in range(t):
        # 核心代码调用
        print(solution(input()))
解法二：使用内置函数pow代替快速幂
# 全局变量
fact = [0] * 501
mod = 1000000007


def initFact():
    fact[0] = 1
    for i in range(1, 501):
        fact[i] = i * fact[i - 1] % mod


def solution(s):
    # 求s串每个字符c的数量
    count = [0] * 26
    for i in range(len(s)):
        count[ord(s[i]) - 97] += 1

    # "出现次数为奇数次的"字符的数量
    odd = 0
    for i in range(26):
        if count[i] % 2 != 0:
            odd += 1

        count[i] //= 2  # 只保留一半字符数量, 后续只需要用到回文串的左半部分，即一半的字符即可

    # 如果"出现次数为奇数次的"字符的数量不止1个，则s串无法重组出回文串
    if odd > 1:
        return 0

    # 不重复的全排列数
    ans = fact[len(s) // 2]
    for i in range(26):
        # 假设 x == fact[count[i] / 2]
        # ans / x % mod
        # 等价于
        # ans * x的乘法逆元 % mod
        # 而x的乘法逆元为 fast_pow(x, mod-2, mod)
        ans = ans * pow(fact[count[i]], mod - 2, mod) % mod

    return ans


if __name__ == '__main__':
    # 初始化1~500的阶乘
    initFact()

    # 输入获取
    t = int(input())
    for _ in range(t):
        # 核心代码调用
        print(solution(input()))

C算法源码

除法取模，乘法逆元，费马小定理，快速幂

#include <stdio.h>
#include <string.h>

#define MAX_LEN 1001
#define MOD 1000000007

long long fact[501] = {0};

void initFact() {
    fact[0] = 1;

    for (int i = 1; i <= 500; i++) {
        fact[i] = i * fact[i - 1] % MOD;
    }
}

// 快速幂算法：用于求解 (a^b) % mod 的结果
long long fast_pow(long long a, long long b) {
    long long ans = 1; // 记录结果

    a %= MOD;

    // 快速幂算法是为了高效计算a^b, 举例
    // 3^5
    //  = 3 * 3^4
    //  = 3 * 9^2
    //  = 3 * 81^1
    //  = 3 * 81 * 81^0
    // 这个过程中如果发现b为奇数，则析出一个底a作为乘数, 实现 b-=1
    // 这个过程中如果发现b为偶数，则底a进行平方运算，实现 b/=2
    // 这个算法求解a^b的时间复杂度为O(log2(b)), 相较于O(b)算法十分高效
    while (b != 0) {
        if (b % 2 == 1) { // 位运算优化： if(b&1 == 1)
            // 3^5 析出来一个3后, 变为 3 * 3^4, 将b值从奇数变为偶数
            // 下面将析出的来3合入结果ans中, 则剩余3^4
            ans = ans * a % MOD;
            // b -= 1; // 可以不用此步, 因为后面b会整除2
        }

        // 3^4 变为 9^2
        a = a * a % MOD; // 底数3 变为 9
        b /= 2; // 幂4 变为 2  // 位运算优化： b>>=1
    }

    return ans;
}

long long solution(char *s) {
    // 求s串每个字符c的数量
    int count[26] = {0};
    for (int i = 0; i < strlen(s); i++) {
        char c = s[i];
        count[c - 'a']++;
    }

    // "出现次数为奇数次的"字符的数量
    int odd = 0;
    for (int i = 0; i < 26; i++) {
        if (count[i] % 2 != 0) {
            odd++;
        }

        count[i] /= 2; // 只保留一半字符数量, 后续只需要用到回文串的左半部分，即一半的字符即可
    }

    // 如果"出现次数为奇数次的"字符的数量不止1个，则s串无法重组出回文串
    if (odd > 1) {
        return 0;
    }

    // 不重复的全排列数
    long long ans = fact[strlen(s) / 2];
    for (int i = 0; i < 26; i++) {
        // 假设 x == fact[count[i] / 2]
        // ans / x % mod
        // 等价于
        // ans * x的乘法逆元 % mod
        // 而x的乘法逆元为 fast_pow(x, mod-2, mod)
        ans = ans * fast_pow(fact[count[i]], MOD - 2) % MOD;
    }

    return ans;
}

int main() {
    // 初始化1~500的阶乘
    initFact();

    // 输入获取
    int t;
    scanf("%d", &t);

    while (t--) {
        char s[MAX_LEN];
        scanf("%s", s);
        // 核心代码调用
        printf("%lld\n", solution(s));
    }

    return 0;
}

C++算法源码

除法取模，乘法逆元，费马小定理，快速幂

#include <bits/stdc++.h>
using namespace std;

#define MOD 1000000007
long long fact[501] = {0};

void initFact() {
    fact[0] = 1;

    for (int i = 1; i <= 500; i++) {
        fact[i] = i * fact[i - 1] % MOD;
    }
}

// 快速幂算法：用于求解 (a^b) % mod 的结果
long long fast_pow(long long a, long long b) {
    long long ans = 1; // 记录结果

    a %= MOD;

    // 快速幂算法是为了高效计算a^b, 举例
    // 3^5
    //  = 3 * 3^4
    //  = 3 * 9^2
    //  = 3 * 81^1
    //  = 3 * 81 * 81^0
    // 这个过程中如果发现b为奇数，则析出一个底a作为乘数, 实现 b-=1
    // 这个过程中如果发现b为偶数，则底a进行平方运算，实现 b/=2
    // 这个算法求解a^b的时间复杂度为O(log2(b)), 相较于O(b)算法十分高效
    while (b != 0) {
        if (b % 2 == 1) { // 位运算优化： if(b&1 == 1)
            // 3^5 析出来一个3后, 变为 3 * 3^4, 将b值从奇数变为偶数
            // 下面将析出的来3合入结果ans中, 则剩余3^4
            ans = ans * a % MOD;
            // b -= 1; // 可以不用此步, 因为后面b会整除2
        }

        // 3^4 变为 9^2
        a = a * a % MOD; // 底数3 变为 9
        b /= 2; // 幂4 变为 2  // 位运算优化： b>>=1
    }

    return ans;
}

long long solution(string &s) {
    // 求s串每个字符c的数量
    int count[26] = {0};
    for (int i = 0; i < s.length(); i++) {
        char c = s[i];
        count[c - 'a']++;
    }

    // "出现次数为奇数次的"字符的数量
    int odd = 0;
    for (int i = 0; i < 26; i++) {
        if (count[i] % 2 != 0) {
            odd++;
        }

        count[i] /= 2; // 只保留一半字符数量, 后续只需要用到回文串的左半部分，即一半的字符即可
    }

    // 如果"出现次数为奇数次的"字符的数量不止1个，则s串无法重组出回文串
    if (odd > 1) {
        return 0;
    }

    // 不重复的全排列数
    long long ans = fact[s.length() / 2];
    for (int i = 0; i < 26; i++) {
        // 假设 x == fact[count[i] / 2]
        // ans / x % mod
        // 等价于
        // ans * x的乘法逆元 % mod
        // 而x的乘法逆元为 fast_pow(x, mod-2, mod)
        ans = ans * fast_pow(fact[count[i]], MOD - 2) % MOD;
    }

    return ans;
}

int main() {
    // 初始化1~500的阶乘
    initFact();

    // 输入获取
    int t;
    cin >> t;

    while (t--) {
        string s;
        cin >> s;
        // 核心代码调用
        cout << solution(s) << endl;
    }

    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1830197.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

LabVIEW程序的常见加密方式

LabVIEW程序的常见加密方式

LabVIEW程序的加密对于保护知识产权和敏感数据至关重要。本文将详细介绍LabVIEW程序常用的加密方式&#xff0c;包括VI加密、代码保护、文件加密和通信加密等&#xff0c;帮助开发者选择合适的加密方法来确保程序的安全性和完整性。 LabVIEW程序的常见加密方式 VI加密&#xf…
阅读更多...
Fiddler抓包工具介绍

Fiddler抓包工具介绍

下载 下载:Web Debugging Proxy and Troubleshooting Tools|Fiddler 进去要填一个表 汉化版 百度网盘 请输入提取码 提取码&#xff1a;xq9t 下载过附件之后分别把两个文件 点开fiddler就ok了 配置https fiddler要想抓到https包(解密的),点击tools->options勾选三个对…
阅读更多...
做好程序前设计

做好程序前设计

不要小看任何一道编程题目&#xff01;一定一定一定要想好之后再动手&#xff01;&#xff01;&#xff01; 带上你的草稿本&#xff01;&#xff01;&#xff01;&#xff01;&#xff01;&#xff01;&#xff01;&#xff01;&#xff01;&#xff01;&#xff01;&#xf…
阅读更多...
DP：01背包问题

DP：01背包问题

一、背包问题的概述 背包问题是⼀种组合优化的NP完全问题。 本质上是为了找出“带有限制条件的组合最优解” 1、根据物品的个数&#xff0c;分为如下几类&#xff1a; • 01背包问题&#xff1a;每个物品只有⼀个&#xff08;重点掌握&#xff09;• 完全背包问题&#xff1…
阅读更多...
牛客热题：最长上升子序列(一)

牛客热题：最长上升子序列(一)

&#x1f4df;作者主页&#xff1a;慢热的陕西人 &#x1f334;专栏链接&#xff1a;力扣刷题日记 &#x1f4e3;欢迎各位大佬&#x1f44d;点赞&#x1f525;关注&#x1f693;收藏&#xff0c;&#x1f349;留言 文章目录 牛客热题&#xff1a;最长上升子序列(一)题目链接方法…
阅读更多...
用PHP来调用API给自己定制一个“每日新闻”

用PHP来调用API给自己定制一个“每日新闻”

头条新闻汇聚了互联网上的时事动态&#xff0c;提供最新新闻动态、网络热门话题和视频更新等&#xff0c;覆盖社会、政治、体育、经济、娱乐、科技等多个领域&#xff0c;并不断刷新内容。企业应用这一接口后&#xff0c;可以快速吸引更多的用户访问自己的平台。即使是非新闻类…
阅读更多...
WINUI——CommunityToolkit.Mvvm Messenger接收消息时报错：Cannot access a disposed object.

WINUI——CommunityToolkit.Mvvm Messenger接收消息时报错：Cannot access a disposed object.

背景 WINUI开发时使用CommunityToolkit.Mvvm的Messemger让UI展示一些信息时出现错误&#xff1a; System.ObjectDisposedException:“Cannot access a disposed object. ObjectDisposed_ObjectName_Name” 详细见下述截图&#xff1a; 开发环境 WIN11 WINUI&#xff13; …
阅读更多...
微信小程序开发系列（三十五）·自定义组件的属性properties

微信小程序开发系列（三十五）·自定义组件的属性properties

微信小程序开发系列&#xff08;三十四&#xff09;自定义组件的创建、注册以及使用&#xff08;数据和方法事件的使用&#xff09;_wx小程序组件开发-CSDN博客 目录 1. 组件的属性 2. 组件的使用 3. 细节描述 1. 组件的属性 Properties是指组件的对外属性&#xff0c;主…
阅读更多...
Nginx之静态文件服务器的搭建

Nginx之静态文件服务器的搭建

1.概述 静态文件服务器是指提供HTML文件访问或客户端 可直接从中下载文件的Web服务器。对于图片、 JavaScript或CSS文件等渲染页面外观的、不会动态改 变内容的文件&#xff0c;大多数网站会单独提供以静态文件服 务器的方式对其进行访问&#xff0c;实现动静分离的架构。 HTML…
阅读更多...
ReactNative和Android通信

ReactNative和Android通信

初始化一个RN项目以后&#xff0c;接下来想要让Android与React Native通信 写一个继承自ReactContextBaseJavaModule类的子类&#xff0c;重写getName方法 package com.awesomeprojectimport android.util.Log import android.widget.Toast import com.facebook.react.bridge.…
阅读更多...
Java并发自测题

Java并发自测题

文章目录 一、什么是线程和进程?线程与进程的关系,区别及优缺点&#xff1f;二、为什么要使用多线程呢?三、说说线程的生命周期和状态?四、什么是线程死锁?如何预防和避免线程死锁?五、synchronized 关键字六、并发编程的三个重要特性七、JMM &#xff08;Java Memory Mod…
阅读更多...
Android 自定义View

Android 自定义View

我们所有的试图都是起源于自定义View&#xff0c;包括ViewGroup也是继承于它&#xff0c;可以说它是视图组件之父。 我们可以从它的大致流程来分为四个部分&#xff1a; 构造方法&#xff0c;onMeasure&#xff0c;onLayout&#xff0c;onDraw 构造方法&#xff1a; 它主要有…
阅读更多...
Java | Leetcode Java题解之第160题相交链表

Java | Leetcode Java题解之第160题相交链表

题目&#xff1a; 题解&#xff1a; public class Solution {public ListNode getIntersectionNode(ListNode headA, ListNode headB) {if (headA null || headB null) {return null;}ListNode pA headA, pB headB;while (pA ! pB) {pA pA null ? headB : pA.next;pB …
阅读更多...
Springmvc接收请求参数

Springmvc接收请求参数

如果你觉得这种限制很麻烦&#xff0c;你可以改为String 因为所有参数在接收的时候原值都是字符串
阅读更多...
Mac | 崩溃分析

Mac | 崩溃分析

一、dump分析 1. 导入符号&#xff1a; ./import_pdb.sh libmedia_stream_ext.dylib.dSYM ./import_pdb.sh libowcr.framework.dSYM 2. 分析dump&#xff1a; ./analyze_dump.sh AE59D64F-0E1D-4A18-8DAF-C2C4D22F9FA6.dmp 3. 第 2 步骤 中会输出崩溃模块、崩溃线程及堆栈…
阅读更多...
使用 Python 进行测试（5）测试的类型

使用 Python 进行测试（5）测试的类型

总结 和我一起唱&#xff01; 冒烟测试&#xff0c;让你快速失败&#xff1b; 回归测试&#xff0c;不打破过去&#xff1b; 健全性检查&#xff0c;保留所拥有&#xff1b; 集成测试&#xff0c;处理副作用&#xff1b; 端到端&#xff0c;永无尽头&#xff01; 回测&#xf…
阅读更多...
SwiftUI 6.0（Xcode 16）全新 @Entry 和 @Previewable 宏让开发妙趣横生

SwiftUI 6.0（Xcode 16）全新 @Entry 和 @Previewable 宏让开发妙趣横生

概览 如火如荼的 WWDC 2024 已进入第五天&#xff0c;苹果开发平台中众多海量新功能都争先恐后的喷薄欲出。 在这里就让我们从中挑两个轻松有趣的新功能展示给小伙伴们吧&#xff1a;它们分别是 全新的 Entry 和 Previewable 宏。 在本篇博文中&#xff0c;您将学到如下内容&a…
阅读更多...
用React编写一个密码组件表单

用React编写一个密码组件表单

theme: condensed-night-purple highlight: atelier-cave-light 背景介绍 我们在使用网站或者应用程序的登录界面或创建帐户界面时&#xff0c;往往避免不了需要用户输入密码这一步骤&#xff0c;而用户是否可以选择看见他们输入的密码是十分重要的一项功能。尤其是在当输入的…
阅读更多...
Focusky是什么软件

Focusky是什么软件

Focusky是一款基于HTML5技术的多媒体演示软件&#xff0c;可以轻松地制作出生动有趣的PPT演示文稿、动画宣传片以及微课。与其他软件相比&#xff0c;Focusky拥有丰富的多媒体资源和动画效果&#xff0c;可以让演示内容更加生动。本文将为您详细介绍Focusky软件的功能&#xff…
阅读更多...
awd工具安装

awd工具安装

fscan(漏洞扫描) 下载 下载地址: Releases shadow1ng/fscan GitHub 把下载的文件放到指定文件目录里, 在文件的位置打开cmd 输入 fscan64.exe -h 192.168.1.1/24 ok了 接下来说说fscan的使用 使用 1.信息搜集: 存活探测(icmp) 端口扫描 2.爆破功能: 各类服务爆破(…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023