前言
直接选择排序也是一个比较简单的排序,所以这里放在第二个进行讲解,这里和冒泡排序是有一点相似。直接选择排序和冒泡排序一样,也是具备一定的教学意义,但是没有什么实际操作的意义,因为直接选择排序的时间复杂度比较高,书写起来和插入排序又差不多,所以没有必要写直接选择排序。
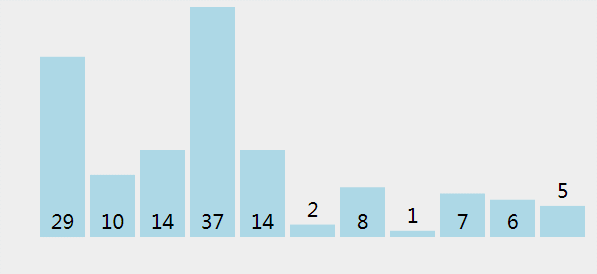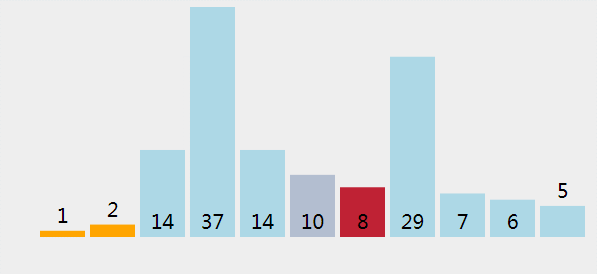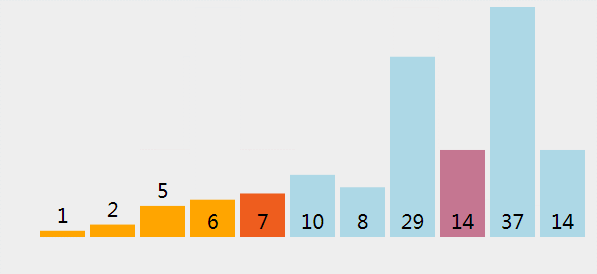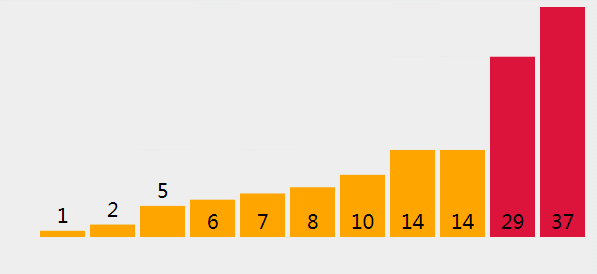
直接选择排序gif
直接选择排序单趟实现
1,初始化min(最小值)=0(也就是最左边的下标)的元素为最小值
2,遍历数组,如果此时出现更小的元素,这个元素的下标是i,那么我们设定min=i
3,之后交换最左边的元素和数值最小元素,因为这个时候我们已经找到下标了
4,最后排序好的最小值放在了最左边,那么此时最左边所在位置不需要进行排序了,分离出来就可以
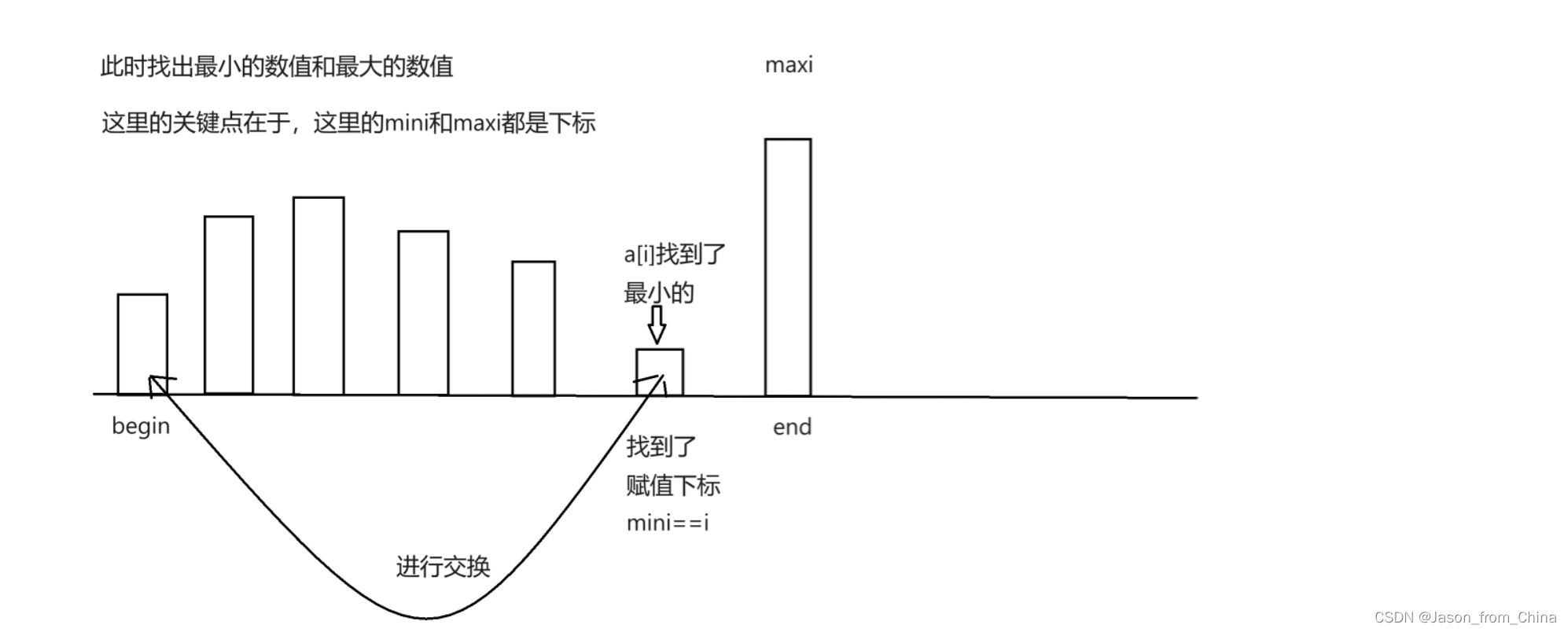
5,这里因为选择排序效率太低了 ,我们稍微进阶一下,我们从两侧开始,选出最小和最大,从而进行交换,虽然没有提高多少效率,但是还是比之前的速度快两倍
直接选择排序注意事项
1,这里begin和end都是外层循环,也就是随着++和--进行缩小差距
2,这里begin和end不是索引,而是缩小差距用的
3,这里是mini和maxi是索引
4,最后交换的时候交换的是下标的元素,不是下标
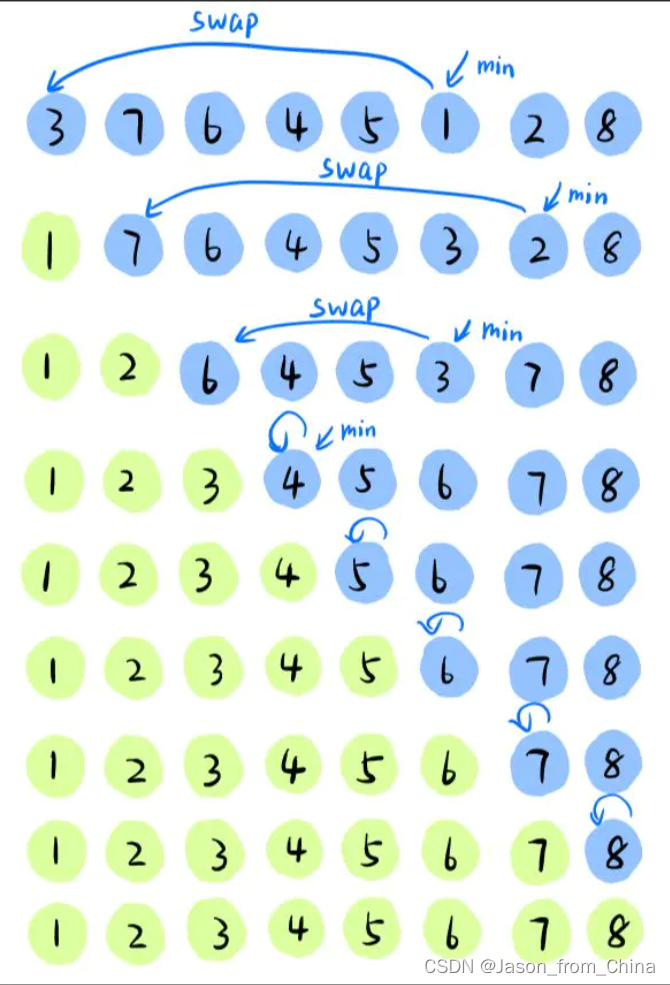
直接选择排序多趟实现图解
直接选择排序代码实现
//交换函数 void Swap(int* p1, int* p2) { int tmp = *p1; *p1 = *p2; *p2 = tmp; } //直接选择排序 void SelectSort(int* a, int n) { //多趟循环 int begin = 0, end = n - 1; while (begin < end) { //单趟循环,找出最小值和最大值 int mini = begin, maxi = end; for (int i = begin; i <= end; i++) { //找到最小值,赋值下标 if (a[i] < a[mini]) { mini = i; } //找到最小值,赋值下标 if (a[i] > a[maxi]) { maxi = i; } } //把最小值和最大值放到开头和结尾去 Swap(&a[mini], &a[begin]); Swap(&a[maxi], &a[end]); begin++; end--; } }解释:
- 外层循环从索引0开始,直到倒数第二个元素。
- 在每次外层循环中,假设当前索引位置的元素是未排序部分的最小值。
- 内层循环从外层循环的下一个位置开始,遍历未排序部分的元素,寻找最小值的索引
minIndex。- 如果找到的最小值不在当前索引位置,使用
Swap函数将其交换到当前索引位置。- 这样,每次外层循环结束时,未排序部分的最小值都被移动到了排序好的部分的末尾。
注意:
- 直接选择排序不是稳定的排序算法,即相等元素之间的相对顺序可能会改变。
- 直接选择排序的时间复杂度是O(n^2),在大多数情况下,它不如其他更高效的排序算法。
- 直接选择排序的空间复杂度是O(1),因为它是原地排序算法。
选择排序时间复杂度计算
外层循环:选择排序算法有一个外层循环,它从第一个元素遍历到倒数第二个元素。这个循环执行了 n−1 次,其中 n 是数组的长度。
内层循环:对于外层循环的每一次迭代,都有一个内层循环,它从当前考虑的元素之后的第一个元素遍历到数组的最后一个元素。在第一次外层循环迭代时,内层循环执行 n−1 次;在第二次迭代时,执行n−2 次;依此类推,直到最后一次迭代,只执行一次。
总迭代次数:内层循环的总迭代次数可以表示为一个等差数列之和: (𝑛−1)+(𝑛−2)+…+2+1=n(n−1)/2
时间复杂度:由于外层循环和内层循环的迭代次数都是 Θ(𝑛)(即线性关系),因此选择排序的总时间复杂度是 Θ(𝑛^2)。
空间复杂度:选择排序是原地排序算法,它只需要一个额外的变量来存储最小元素的索引,因此空间复杂度是 Θ(1)。