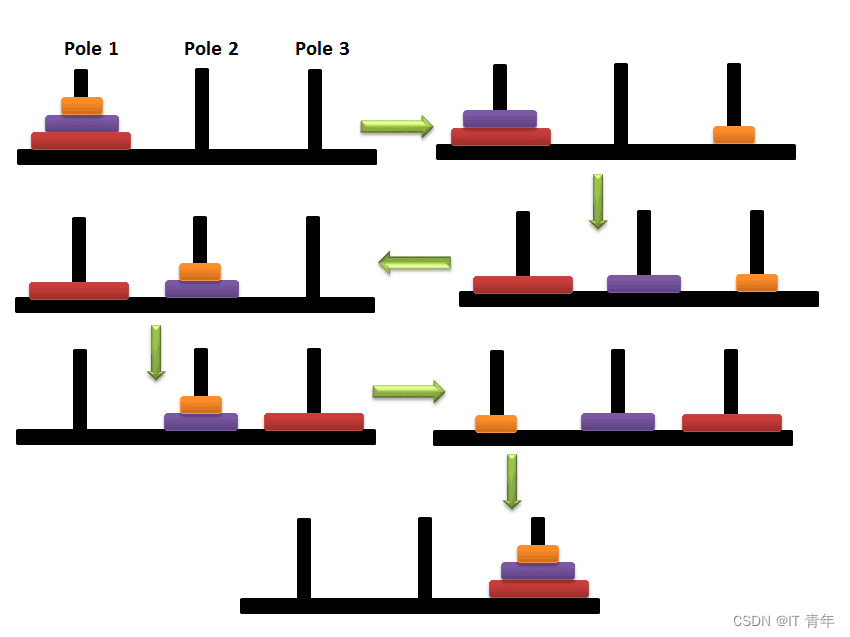
一、 问题描述  

 二、算法思想  

1. 首先定义一个函数，接收四个参数：n表示当前需要移动的盘子数量，A表示起始基座，B表示目标基座，C表示辅助基座。

2. 在函数内部，首先判断如果n为1，即只有一个盘子需要移动，直接将盘子从起始基座移动到目标基座即可，输出移动的步骤。

3. 如果n大于1，则先将n-1个盘子从起始基座移动到辅助基座，此时可以借助目标基座作为辅助基座，这样可以保证大盘子在下，小盘子在上。具体的移动步骤可以通过递归调用这个函数来实现。

4. 然后输出将第n个盘子从起始基座移动到目标基座的步骤。

5. 最后将n-1个盘子从辅助基座移动到目标基座，也是通过递归调用这个函数来实现。

三、代码实现 

#include<stdio.h>
void hanio(int n,char A,char B,char C)
{
    if(n==1)
    {
        printf("%c->%c\n",A,C);
    }
    else{
        hanio(n-1,A,C,B);
        printf("%c->%c\n",A,C);
        hanio(n-1,B,A,C);
    }
}
int main()
{
    int num;
    scanf("%d",&num);
    hanio(num,'A','B','C');
    return 0;
}

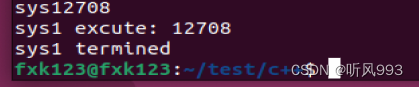
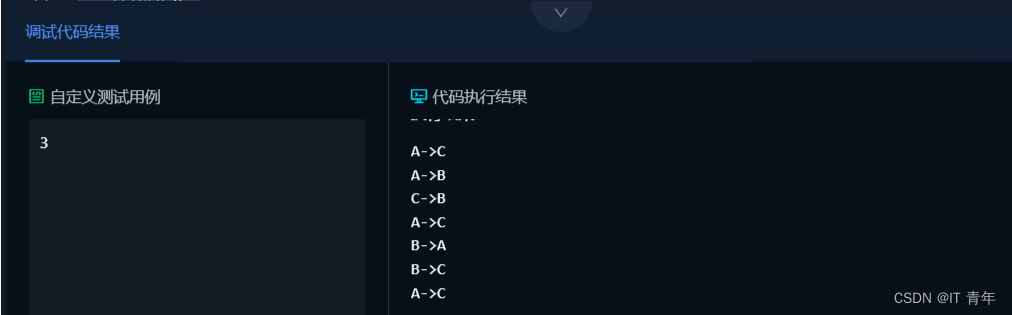
执行结果 

 结语   

当你坚持不下去的时候

就是坚持开始的时刻

！！！