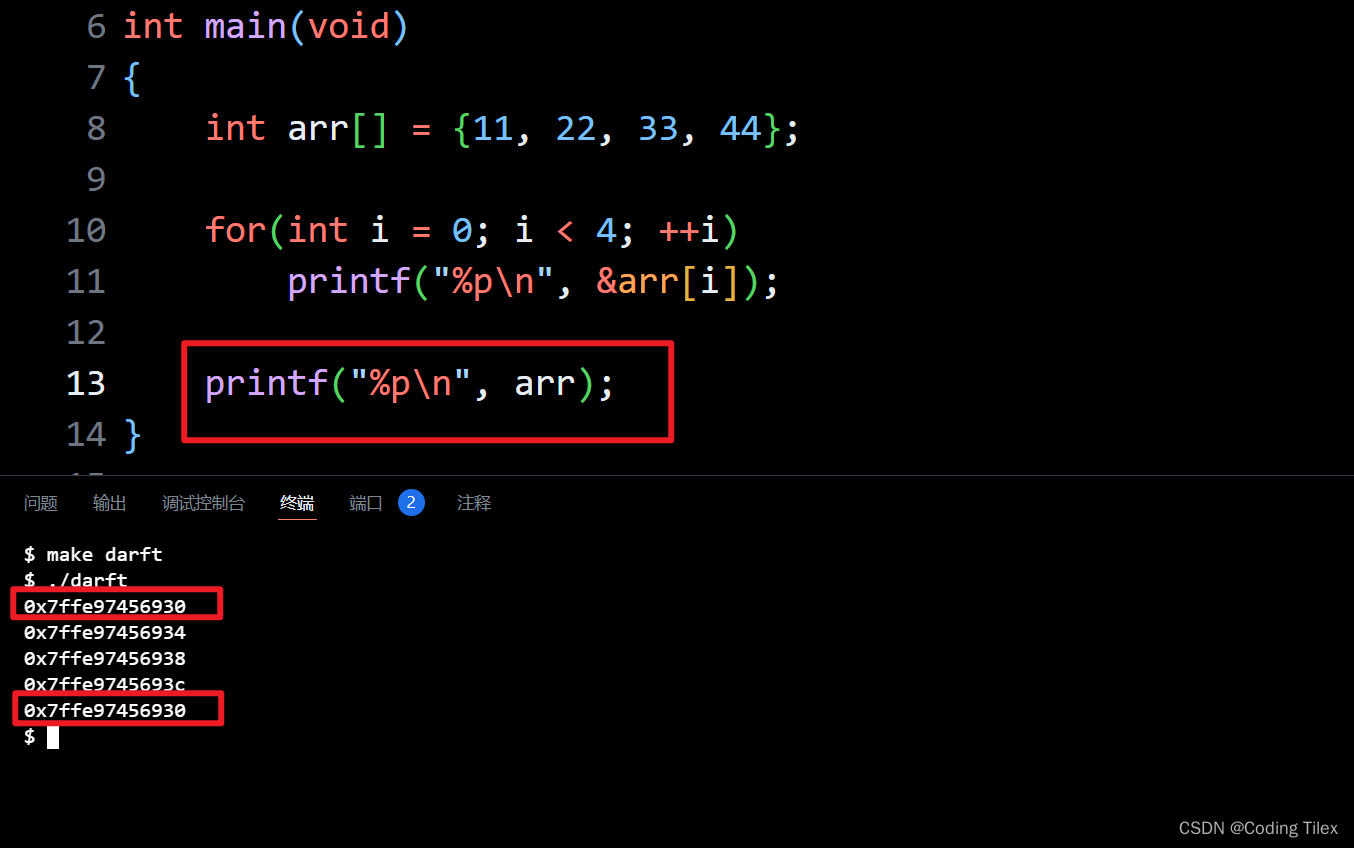
题目链接：
题目描述：某二叉树的先序遍历结果记录于整数数组 preorder，它的中序遍历结果记录于整数数组 inorder。请根据 preorder 和 inorder 的提示构造出这棵二叉树并返回其根节点。

注意：preorder 和 inorder 中均不含重复数字。

例子1：

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]

输出: [3,9,20,null,null,15,7]

示例2：

输入: preorder = [-1], inorder = [-1]

输出: [-1]

数据范围：

1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
inorder 均出现在 preorder
preorder 保证 为二叉树的前序遍历序列
inorder 保证 为二叉树的中序遍历序列

理论知识：

先序：根左右
中序：左根右
后序：左右根
1、已知先序和中序能唯一确定一颗二叉树。
2、已知中序和后序能唯一确定一颗二叉树。
3、已知先序和后序 不能 唯一确定一颗二叉树。

思路：有前备知识我们很快能发现，先序主要作用是确定根，先序中的每个节点都会顺序的成为从上往下的子树的根节点；而通过先序中确定的根节点，在中序序列中，我们能够将二叉树进行初步划分左右子树，然后继续找先序中的根，继续划分左右子树，划分这个过程可以借助递归完成。这里面涉及到的问题点就是，不断找到根节点之后，在中序中找寻左右区间的问题。因此，为了直观一点，我们可以借助map来存储每个节点在数组中对应的顺序下标。这样，在找寻到一个根节点的时候，通过这个根节点所在中序中的位置确定下一次划分的区间。
代码：

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */

 var (
    preIndex = 0 // 维护在递归时候获取先序的下一个节点
    inVal2IndexMap map[int]int // 维护中序序列中每个元素的对应的下标
 )
func deduceTree(preorder []int, inorder []int) *TreeNode {
    preIndex = 0 // 注意全局变量加载时机，载入这个文件进行多组输入时候，全局变量会一直未被重置
    // 标记每个中序数字所在的位置，方便通过先序递归时候划分边界
    inVal2IndexMap = make(map[int]int, len(inorder))
    for idx, val := range inorder {
        inVal2IndexMap[val] = idx
    }
    return reBuildTree(preorder, 0, len(inorder))
}

func reBuildTree(preorder []int, left, right int) *TreeNode{
    // 该子树没有子节点
    if left == right {
        return nil
    }
    // 构造当前的根节点，下标为preIndex
    root := &TreeNode{Val:preorder[preIndex]}
    // 找到先序这个根节点在中序中的位置
    inIndex := inVal2IndexMap[root.Val]
    preIndex++
    // 递归构造左子树
    root.Left = reBuildTree(preorder, left, inIndex)
    // 递归构造右子树 
    root.Right = reBuildTree(preorder, inIndex+1, right)
    
    return root
}

当然，上面借助了map，我们也可以不用借助额外的存储结构来实现程序。

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */

func deduceTree(preorder []int, inorder []int) *TreeNode {
    for k := range inorder {
        if inorder[k] == preorder[0] {
            return &TreeNode{
                Val: preorder[0],
                Left: deduceTree(preorder[1:k+1], inorder[0:k]),
                Right: deduceTree(preorder[k+1:], inorder[k+1:]),
            }
        }
    }
    return nil
}