高级人工智能复习题目整理中科大

题目整理

填空

在这里插入图片描述
1.准确性，复杂性，验证集
2. $3^{2^n}$ $3^{C^m_{2n}}$ $3^m$ $n + 1$
3. 状态从状态s采取行动a后继续采用策略 $\pi$ 的收益环境
4. 语法语义推理规则
5. 参与者，策略集，收益，参与者们选择的策略互为最佳应对
6. sigmod,tanh,ReLu
7. KNN,决策树

问答

在这里插入图片描述
(1) 11;
(2)1+2+4+6+9+11=33 存疑（博客答案是34，我觉得是33）
(3)1+2+4+7=14

（9）启发式搜索假设有N个红军和N个蓝军，船每次最多可供K个人乘渡，这里 $\le3$ 。假设在某个时刻，在河的左岸有M个红军，C个蓝军，B=1表示船在左岸，B=0表示船在右岸。现在以它们的组合为状态 $n = (M, C, B)$ 的描述。给定下面的两种不同的启发式函数：
$h_1(n)=M+C / h_2(n)=M+C-2B$
请说明 $h_1(n)$ 不满足 $h_1(n) \le h^*(n)$ 而 $h_2(n)$ 满足

解：
离目标越近，启发式函数应该越小
$h_2(n)$ 考虑了船的位置问题，船在左岸的时候， $h_1(n)$ 高估了

（10）概念题：谈谈你对搜索问题，MDP，强化学习，完美信息下的动态博弈和非完美信息下的动态博弈的理解，分析它们之间的异同。

解：

搜索问题：
行动是确定让搜索沿一条边前进
解是一条路径或状态序列

MDP
行动随机地让搜索沿多条变前进
解不是路径而是策略，一组从装填到行动的映射关系

MDP和强化学习

MDP：转移概率和奖励情况已知，离线；判断和决策都可以仿真；f已知
强化学习：转移概率和奖励未知，在线；需要花费代价去探索未知；f未知

完美信息的动态博弈：每个参与者知道所有的公共信息，将对手视为MDP建模中无法观测和了解的位置因素
非完美信息下的动态博弈：可以看做强化学习，不知道转移概率和每一步的奖励，需要逐步了解和学习

博弈问题也可以建模为搜索问题

（11）概念题：简述过拟合产生的原因，通过修改损失函数可以避免过拟合，举两个例子说明这种方法。

过拟合产生的主要原因是训练数据过少或模型过于复杂

通过修改损失函数可以避免过拟合，如
1.L2正则化：
通过在Loss的基础上增加权重参数的平方和项，从而惩罚权重参数过大的情况。
$Loss_2=Loss+\lambda \sum \theta_j^2$

2.L1正则化：
通过在Loss的基础上增加权重参数的绝对值和项，从而惩罚权重参数非零的情况。

在这里插入图片描述

(1) PPT上有（复习部分有图）
(2)
假设输出层误差为1，即 $\delta_{\text{score}} = 1$ 。

计算输出层梯度：
$\frac{\partial \text{loss}}{\partial w} = -\lambda_0 y [h_1, h_2]$
隐藏层误差传播到输出层：
$\delta_{h_j} = \delta_{\text{score}} \cdot w_j \cdot h_j \cdot (1 - h_j)$
其中， $\delta_{\text{score}} = 1$ ，因此：
$\delta_{h_j} = w_j \cdot h_j \cdot (1 - h_j)$
计算隐藏层梯度：
$\frac{\partial \text{loss}}{\partial v_j} = \delta_{h_j} \cdot \phi(x)$
即：
$\frac{\partial \text{loss}}{\partial v_j} = (w_j \cdot h_j \cdot (1 - h_j)) \cdot \phi(x)$

参数更新
根据梯度下降法，更新权重参数 (V) 和 (W)：

对于 (w)：
$\lambda_0 \cdot \frac{\partial \text{loss}}{\partial w}$
其中：
$\frac{\partial \text{loss}}{\partial w} = -\lambda_0 y [h_1, h_2]$
对于 (v_j)：
$v_j := v_j - \lambda_0 \cdot \frac{\partial \text{loss}}{\partial v_j}$
其中：
$\frac{\partial \text{loss}}{\partial v_j} = (w_j \cdot h_j \cdot (1 - h_j)) \cdot \phi(x)$

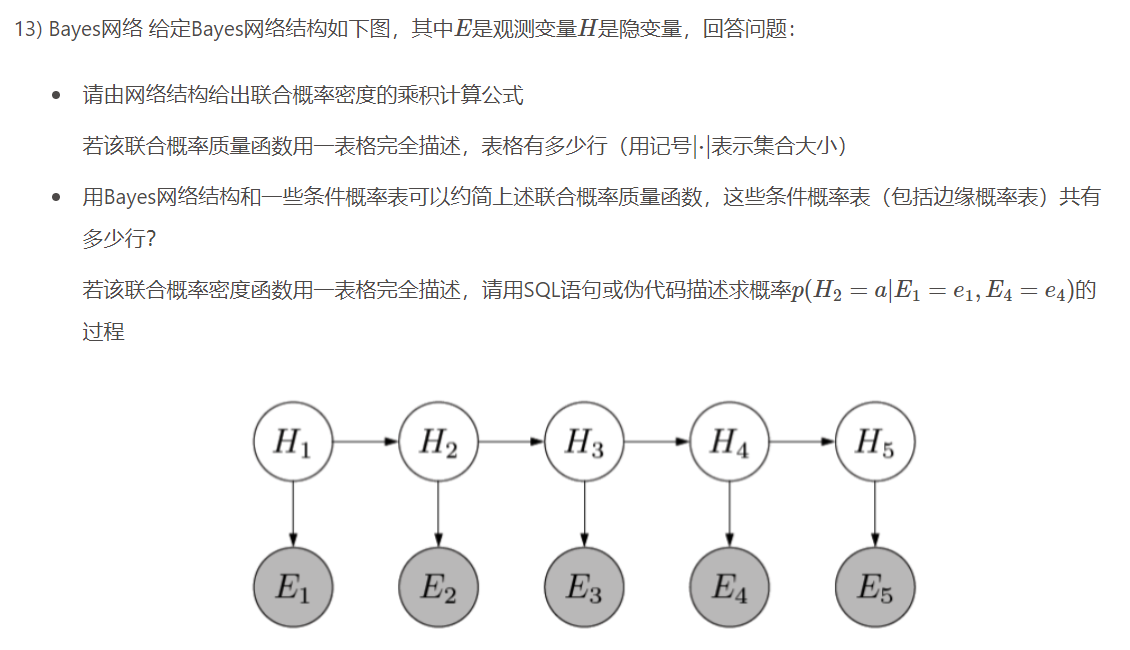
在这里插入图片描述
(1) $p(E1,…E_n,H_1,…H_n)=p(H_1)\prod_{i=2}^5p(Hi|H{i-1})\prod_{i=1}^5p(E_i|H_i)$
(2) $\prod_i|H_i||E_i|$
(3) $|H_1|+\sum_{i=2}^5|H_i||H_i-1| +\sum_{i=1}^5 |E_i||H{i-1}|$
(4)

c1,c2=0,0
for i in data:
	if i satisfy(E=e):
		c1+= p(X_i)
		if i satisfy (Q=q):
			c2+=p(X_i)
return c1/c2

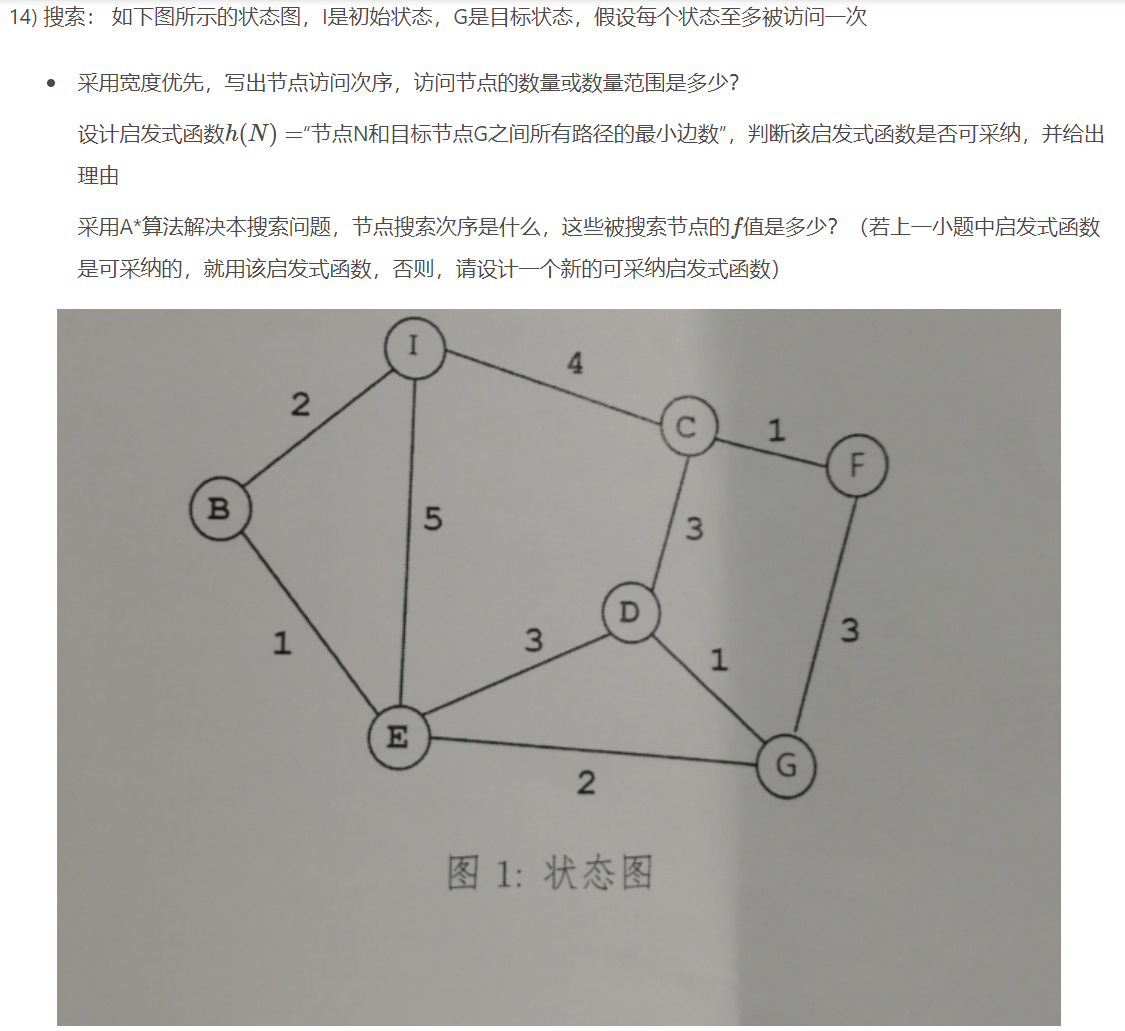
在这里插入图片描述
（1）I->BEC->DFG 7 个节点
（2）可采纳，设N到G的最优路径的每条边权值为 $p_i$
共𝑘条边，由于 $p_i \ge 1$ ，则 $\sum p_i \ge k$ ，由此： $\le H^*(N)$ ，得证
（3）I->B->E->G
f=3？

(15)岭回归问题。求解线性回归问题是, $\hat{W}=\arg min_W|y-XW|^2+\lambda|W|^2$ 。其中 $X\in R^{n*d}$ 是n个d维的数据，X每列和为0，且 $\in R^n,W\in R^n$ 是参数向量。岭回归问题就是寻找最优参数 $\hat{W}$ 使得损失函数和 $L_2$ 正则化项的线性组合构成的目标函数最小。请用矩阵运算，给出最优解 $\hat{W}$ 的结算过程和结果

解：

我们可以使用矩阵运算来求解最优参数 $\hat{W}$ 。

定义目标函数：
$\|y - XW\|^2 + \lambda \|W\|^2$
其中，
$\|y - XW\|^2 = (y - XW)^\top (y - XW)$
$\|W\|^2 = W^\top W$
展开目标函数：
$XW)^\top (y - XW) + \lambda W^\top W$
$y^\top y - 2y^\top XW + W^\top X^\top XW + \lambda W^\top W$
求解梯度：
对 (W) 求偏导数并使其等于零：
$\frac{\partial J(W)}{\partial W} = -2X^\top y + 2X^\top XW + 2\lambda W = 0$
解方程：
$(X^\top X + \lambda I)W = X^\top y$
其中， $I$ 是 $\times d$ 的单位矩阵。
求解最优参数：
$\hat{W} = (X^\top X + \lambda I)^{-1} X^\top y$

赛马时，一线人会在赛前告诉你某匹马Belle没吃早餐。假设：

马输赢取决于其健康和速度，而健康和速度无关。
健康的马比病马吃早餐的概率大
线人情报的可靠性不是100%
求解下列问题：
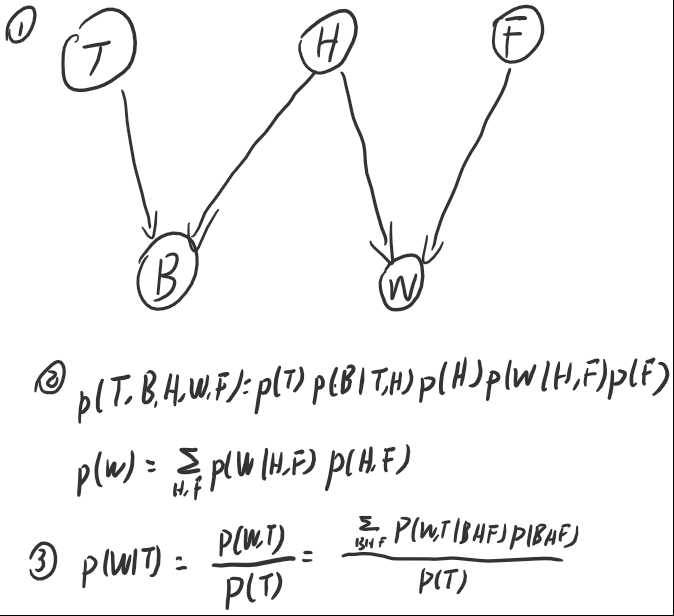
画出5个变量的贝叶斯网络，其中T:得到情报，B:Belle吃早餐，H:Belle健康，W:Belle赢，F:Belle很快
根据贝叶斯网络结构，给出联合概率 $p (T, B, H, W, F)$ 的乘积计算公式。给出边缘概率 $p (W)$ 的计算公式
计算条件概率 $p (W ∣ T)$ ，即依据线人情报来计算Belle获胜的概率
在这里插入图片描述
17) 学习问题：

写出线性回归和逻辑斯蒂回归的目标函数
写出SVM的目标函数
写出加入松弛变量后的SVM的优化目标

解：
（1）线性回归的目标函数

线性回归的目标是通过最小化预测值和真实值之间的均方误差来拟合一条直线。目标函数可以表示为：

$\frac{1}{2} \sum_{i=1}^{n} (y_i - X_iW)^2$

其中，

( y_i ) 是第 ( i ) 个样本的真实值，
( X_i ) 是第 ( i ) 个样本的特征向量，
( W ) 是参数向量。

可以用矩阵形式表示为：

$\frac{1}{2} \| y - XW \|^2$

（2）逻辑斯蒂回归的目标函数

逻辑斯蒂回归的目标是通过最大化训练样本的似然函数（或最小化负对数似然函数）来拟合一个分类模型。目标函数可以表示为：

$-\sum_{i=1}^{n} \left[ y_i \log(h(X_iW)) + (1 - y_i) \log(1 - h(X_iW)) \right]$

其中，

( y_i ) 是第 ( i ) 个样本的标签（0 或 1），
( X_i ) 是第 ( i ) 个样本的特征向量，
( h(z) = \frac{1}{1 + e^{-z}} ) 是sigmoid函数。

可以用矩阵形式表示为：

$-\left[ y^\top \log(h(XW)) + (1 - y)^\top \log(1 - h(XW)) \right]$

（3）支持向量机（SVM）的目标函数

线性SVM的目标是通过最大化类别间的间隔来拟合一个分类模型。标准的无松弛变量SVM的目标函数可以表示为：

$\min_W \frac{1}{2} \|W\|^2$
$\text{subject to } y_i (X_i W + b) \ge 1 \quad \forall \ i$

其中，

( y_i ) 是第 ( i ) 个样本的标签（+1 或 -1），
( X_i ) 是第 ( i ) 个样本的特征向量，
( W ) 是参数向量，
( b ) 是偏置项。

（4）加入松弛变量后的SVM的优化目标

加入松弛变量（slack variables）后的软间隔SVM的目标函数可以表示为：

$\min_{W, \xi, b} \frac{1}{2} \|W\|^2 + C \sum_{i=1}^{n} \xi_i$
$\text{subject to } y_i (X_i W + b) \geq 1 - \xi_i \quad \forall i$
$\xi_i \geq 0 \quad \forall i$

其中，

(\xi_i) 是松弛变量，表示第 ( i ) 个样本的误差，
( C ) 是惩罚参数，控制间隔与误分类的权衡。

线性回归：最小化均方误差。
逻辑斯蒂回归：最小化负对数似然。
SVM（无松弛变量）：最小化参数范数，要求所有样本严格正确分类。
SVM（有松弛变量）：在最小化参数范数的同时，加上松弛变量项，允许部分样本误分类，增加模型的柔韧性。

回忆2023

（1）信息熵公式： $H(N)=-\sum_i p_i \log(p_i)$
$p_i$ 是节点N中拥有数据集D中属于第i类数据在D中占比。

（2）hinge损失函数: $max(1-W\phi(x)y,0)$

（3）约束求解问题的(X,D,C)的含义:
一个CSP问题是一个三元组 $(X, D, C)$ ，其中 $X$ 是一组变量； $D$ 是值域； $C$ 是一个约束组，包含了 $m$ 个约束 $X$ 分量间取值关系的计算公式。
$X_i$ 从 $D_i$ 中取值，所有变量都给一个取值，形成一个赋值 $v=(x_1,x_2,...,x_3)$ 可以参与约束 $C$ 的计算，判断约束是否被满足

（4）无限集合有k个球，球的分布是什么样子的时候熵最大：
在信息理论中，熵（entropy）是用来度量随机变量不确定性的一个指标。给定一个有限或无限的集合，当我们讨论分布的熵时，通常是指其概率分布的熵。对于无限集合中的球，最常见的考虑是概率分布的情况。

解：
假设我们有 ( k ) 种不同类型的球，并且球的集合是无限的。我们需要考虑这些球的分布方式使得熵最大化。

每个类型的球概率相等：
- 如果每种类型的球出现的概率相等，那么我们可以假设每种类型的球出现的概率为 ( \frac{1}{k} )。
- 这意味着每种类型的球都是均匀分布的。
- 这样的均匀分布最大化了熵，因为熵在均匀分布时是最大的。

[ p(x_i) = \frac{1}{k} ]

熵的计算：
- 对于均匀分布的情况，熵的计算如下：
  [ H(X) = -\sum_{i=1}^{k} \frac{1}{k} \log \frac{1}{k} ]
- 由于对每种类型的球的概率都是 ( \frac{1}{k} )，我们可以简化熵的公式：
  [ H(X) = -k \left( \frac{1}{k} \log \frac{1}{k} \right) = \log k ]

所以，对于无限集合中的 ( k ) 种球，当每种类型的球的概率分布均匀时，熵最大。

（5）迭代深度优先搜搜的时空复杂度：
访问节点数 $O(b^d)$ 空间复杂度 $O (b d)$

（6）决策树通过什么防止过拟合
剪枝

（7）贝叶斯网络是不是有监督的机器学习方法、EM算法是不是无监督的机器学习算法
是；是

（8）深度优先搜索和回溯法的异同；

深度优先搜索和回溯法都是用于解决问题的搜索算法，它们在某些方面相似，但在其他方面又有一些不同之处。

相同点：

搜索方式：两者都是基于搜索树的算法，都通过探索搜索空间中的不同节点来找到解决问题的答案。

递归性质：深度优先搜索和回溯法都具有递归的特点，它们在搜索过程中会不断地深入到搜索树的分支中。

不同点：
,回溯法在求解过程中不保留完整的树结构,而深度优先搜索则记下完整的搜索树

目标：深度优先搜索通常用于找到搜索树中的一个解，而回溯法更多地用于找到搜索树中的所有解。

回溯机制：回溯法在搜索的过程中，当发现当前路径不能满足问题的要求时，会回溯到上一个状态，并尝试其他分支。而深度优先搜索并没有显式的回溯机制，它只是沿着一条路径一直深入到底部，直到找到解或者无法继续为止。

空间复杂度：在空间复杂度上，回溯法通常需要更多的内存，因为它需要在递归调用中保存更多的状态信息，而深度优先搜索则相对较少，因为它只需要保存当前的路径信息。

（9）博弈的组成成分；
参与者；策略集；收益

（10）搜索算法的局部算法跟全局算法的区别，举例说明。
解：
搜索算法可以分为局部算法和全局算法，它们在搜索问题空间时的策略和范围上有所不同。

局部算法：

局部算法通常只关注当前状态的邻域，并在邻域内搜索最优解。它们不考虑整个问题空间，而是通过一系列局部决策逐步改进当前解，直到达到某种终止条件或者找到满意的解为止。局部算法往往更加高效，尤其适用于大规模问题，因为它们不需要考虑整个问题的状态空间。

例子：

爬山算法（Hill Climbing）：该算法通过不断选择当前状态的邻域中使目标函数值最大的状态来进行搜索。它只考虑了局部最优解，可能会陷入局部最优解而无法找到全局最优解。

模拟退火算法（Simulated Annealing）：模拟退火算法也是一种局部搜索算法，它以一定概率接受比当前解更差的状态，以避免陷入局部最优解。

全局算法：

全局算法考虑整个问题空间，并在其中搜索全局最优解。它们可能会更加耗时，因为它们需要考虑整个问题空间，并尝试各种可能的组合和路径。

例子：

启发式搜索算法（Heuristic Search）：启发式搜索算法是一种全局搜索算法，它使用启发式函数来指导搜索过程，以便更加有效地在整个问题空间中搜索解。例如，A*算法是一种启发式搜索算法，通过估计到目标的距离来选择下一步的搜索路径。

遗传算法（Genetic Algorithm）：遗传算法是一种全局优化算法，通过模拟自然选择和遗传机制来搜索问题空间中的最优解。遗传算法尝试在整个搜索空间中进行交叉和变异，以找到适应度最高的解。

（11）贝叶斯网络，画因果图，求简单的条件概率分布和边缘分布。

（12）强化学习，给出一张图，包括了状态、行动、转移概率、收益、策略，第一问算状态点的V值；第二问求出更新之后的策略。（记住Q、V的更新公式就会写）

解

第一问：

我们需要计算每个状态点的 V 值，根据贝尔曼方程的更新规则，V 值更新公式为：

$\sum_{a} \pi(a|s) \sum_{s',r} p(s',r|s,a) [r + \gamma V(s')]$

其中，[ \pi(a|s) ] 是策略函数，[ p(s’,r|s,a) ] 是转移概率函数，[ \gamma ] 是折扣因子。

第二问：

更新策略需要根据 Q 值，Q 值的更新公式为：

$\sum_{s',r} p(s',r|s,a) [r + \gamma \max_{a'} Q(s',a')]$

然后根据更新后的 Q 值选择新的策略。策略更新规则可以是ε-贪心策略、Softmax 策略等。

在这里插入图片描述

（13）神经网络，给出一个三层的网络图，各层的激活函数和损失函数，第一问求反向传播的权重更新公式，第二问代入数据计算更新后的权重，第三问问学习率的大小给训练带来的影响。这一题网络输入层2个节点，隐层三个节点，输出层一个节点。

解：

第一问：

反向传播的权重更新公式可以使用梯度下降法。假设损失函数为 L，学习率为 (\alpha)，那么权重更新的公式如下：
$W_{ij}^{(l)} = W_{ij}^{(l)} - \alpha \frac{\partial L}{\partial W_{ij}^{(l)}}$

其中，( W_{ij}^{(l)} ) 表示第 (l) 层的权重矩阵的第 (i) 行第 (j) 列元素。

第二问：

代入数据计算更新后的权重需要具体的网络结构和损失函数。根据网络结构和损失函数的不同，反向传播的计算方法也会有所不同。

第三问：

学习率的大小会直接影响权重的更新速度和稳定性。如果学习率过大，可能导致权重更新过快，甚至无法收敛；而学习率过小，则可能导致收敛速度过慢。通常需要通过实验来选择合适的学习率，以保证模型能够快速收敛到最优解。

（14）KNN近邻，给出五个数据点(x1,x2)和他们的label，给出一个待分类的数据，第一问问待分类的数据在不同的k值下分成什么类；第二问问k的取值有什么影响。

解：

第一问：

我们需要根据不同的 k 值，使用KNN算法对待分类的数据点进行分类。KNN算法的步骤是：

计算待分类数据点与已知数据点之间的距离。
选择最近的 k 个数据点。
统计这 k 个数据点的类别，并选择其中出现次数最多的类别作为待分类数据点的类别。

不同的 k 值可能导致不同的分类结果。常见的 k 值包括 1、3、5 等。我们可以尝试这些 k 值，来观察分类结果。

第二问：

K 的取值会直接影响到分类的结果。较小的 k 值可能会导致模型对噪声数据敏感，容易受到局部的影响，可能会产生过拟合；而较大的 k 值可能会导致模型过于简单，忽略了局部结构，可能会产生欠拟合。

总的来说，适当选择 k 值很重要，需要根据具体的数据集和问题来确定。通常需要通过交叉验证等方法来选择最优的 k 值。

回忆2021

（1）策略函数值迭代的Bellman递推公式

（2）LSTM比RNN增加了——和哪——三个门

（3）给出近似逼近的线性权系数，特征提取函数

解：

为了通过近似逼近的方法求解线性权系数，我们通常使用线性回归或其他线性模型。这里给出一个简单的例子，说明如何使用线性回归来近似逼近权系数，并介绍特征提取函数。

线性回归模型

假设我们有一个输入特征向量 (\mathbf{x} = [x_1, x_2, \ldots, x_n]) 和对应的目标值 (y)。线性回归模型可以表示为：

$\mathbf{w}^T \mathbf{x} + b$

其中：

(\mathbf{w} = [w_1, w_2, \ldots, w_n]) 是需要学习的权重向量。
(b) 是偏置项。

求解线性权系数

为了求解线性权系数 (\mathbf{w}) 和偏置项 (b)，我们最小化以下损失函数（均方误差）：
$L(\mathbf{w}, b) = \frac{1}{m} \sum_{i=1}^m (y_i - (\mathbf{w}^T \mathbf{x}_i + b))^2$

其中，(m) 是样本数量，(\mathbf{x}_i) 是第 (i) 个样本的特征向量，(y_i) 是第 (i) 个样本的目标值。

通过求解这个最小化问题，我们可以得到近似逼近的线性权系数 (\mathbf{w}) 和偏置项 (b)。

特征提取函数

特征提取函数的目的是将原始数据转换为适合模型训练的特征。特征提取函数通常根据具体的问题和数据类型来设计。下面是几个常见的特征提取方法：

多项式特征提取：
将输入特征扩展为多项式形式。例如，给定输入特征 (\mathbf{x} = [x_1, x_2])，我们可以生成二次特征：
[ \phi(\mathbf{x}) = [1, x_1, x_2, x_1^2, x_2^2, x_1 x_2] ]
离散特征编码（One-hot Encoding）：
对于分类变量，我们使用独热编码将每个类别转换为二进制向量。例如，给定一个分类变量 (color) 有三个取值 {red, green, blue}，独热编码将其转换为：
[ \text{red} \rightarrow [1, 0, 0], \quad \text{green} \rightarrow [0, 1, 0], \quad \text{blue} \rightarrow [0, 0, 1] ]
归一化和标准化：
对于数值特征，我们通常需要进行归一化或标准化处理，以确保特征具有相似的尺度。例如，标准化将特征值减去均值并除以标准差：
[ x_i’ = \frac{x_i - \mu}{\sigma} ]

（4）MDP的一个实例计算题，计算一个策略的V值

（5）解释策略评估函数V（）和Q（）的区别
策略评估中的 ( V ) 函数和 ( Q ) 函数是强化学习中的两个关键概念，用于评估在给定策略下的状态或状态-动作对的价值。它们的区别在于评估的对象和具体的定义：

关系和区别

评估对象：
- ( V(s) ) 评估的是在状态 ( s ) 下的预期价值。
- ( Q(s, a) ) 评估的是在状态 ( s ) 下执行动作 ( a ) 的预期价值。
公式关系：（PPT上是是max）
- 状态价值函数 ( V(s) ) 可以通过状态-动作价值函数 ( Q(s, a) ) 计算得到：
  [
  V^\pi(s) = \sum_{a \in A} \pi(a|s) Q^\pi(s, a)
  ]
- 状态-动作价值函数 ( Q(s, a) ) 可以通过状态价值函数 ( V(s) ) 表示：
  [
  Q^\pi(s, a) = \mathbb{E} \left[ R_{t+1} + \gamma V^\pi(S_{t+1}) \mid S_t = s, A_t = a \right]
  ]
作用：
- ( V(s) ) 用于评估在某一状态下的总体价值，它告诉我们某个状态有多好。
- ( Q(s, a) ) 用于评估在某一状态下执行某个动作的价值，它告诉我们在某个状态下采取某个动作有多好。

（6）线性分类和线性回归的几何意义分别是

线性回归：几何上，线性回归试图找到一条直线（或超平面），以最小化预测值与实际值之间的误差。

线性分类：几何上，线性分类试图找到一个直线（或超平面），以最大化将不同类别数据点分开的间隔。

这两者的主要区别在于，线性回归处理的是连续型输出变量，而线性分类处理的是离散型输出变量。

（7）写出岭回归求导过程，写出目标函数更新的伪代码

# 初始化权重向量 w 为零向量
Initialize w as zero vector of size m

# 迭代更新权重向量
For iteration = 1 to num_iterations:
    # 计算预测值
    y_pred = X * w

    # 计算误差
    error = y - y_pred

    # 计算梯度
    gradient = -2 * (X^T * error) + 2 * lambda * w

    # 更新权重
    w = w - learning_rate * gradient

End For

Return w

（8）计算一个二维卷积

（9）约束满足和优化问题与搜索问题的区别体现在关于的解形式化上有什么不同

约束满足问题的解通常是一组数值的集合，它们满足所有给定的约束条件。
优化问题的解是使得目标函数达到最优值的点、向量或结构，其数学表达是问题的目标函数及其约束条件的函数形式。
搜索问题的解是满足搜索目标的一组状态、路径、规划或决策，通常表示为一系列动作、状态转换或决策序列。

（10）贝叶斯，根据拉普拉斯平滑计算边缘和条件概率表，计算一个具体的条件概率值

（11）解释A*和贪婪算法的区别

考虑因素不同：

贪婪算法只考虑了当前步骤的局部最优解，没有考虑全局最优解。
A*算法综合考虑了已经花费的代价和估计剩余代价，从而更倾向于选择全局最优解。

性能保证不同：

贪婪算法不能保证找到最优解，因为它只考虑了当前步骤的局部最优解。
A*算法在满足一定条件下（如启发函数满足一定性质），可以保证找到最优解。

时间和空间复杂度不同：

贪婪算法通常具有较低的时间和空间复杂度，因为它只考虑了当前步骤的局部最优解。
A*算法通常具有较高的时间和空间复杂度，因为它需要综合考虑已经花费的代价和估计剩余代价，并维护一个优先队列。

（12）写出三个激活函数sigmod tang ReLu的表达式，画出曲线图
https://www.cnblogs.com/kang06/p/9371420.html

（13）贝叶斯网，一小问如是：试用伪码描述，应用变量消元法求p(h1|e3e5)的过程

# 变量消元法求解 P(h1 | e3, e5)
Input: Bayesian network BN, evidence variables e3, e5, query variable h1
Output: Probability P(h1 | e3, e5)

# 1. 初始化因子集合为所有因子
factors = BN.factors()

# 2. 对每个证据变量 e in {e3, e5}：
    # 2.1 找到与 e 相关的因子 f_e，并将其固定为给定值
    factors.fix_value_for_variable(e)

# 3. 对每个非证据变量 X：
    # 3.1 构建 X 的新因子 f_X，并对它进行消元操作
    factors.eliminate_variable(X)

# 4. 规范化计算目标条件概率
h1_factor = factors.find_factor_for_variable(h1)
normalize(h1_factor)

# 5. 返回目标条件概率 P(h1 | e3, e5)
return h1_factor