一、研究背景及其意义

家庭资产分析在现代经济学中的重要性不仅限于单个家庭的财务健康状况，它还与整个经济体的发展紧密相关。家庭资产的增长通常反映了国家经济的整体增长，而资产分布的不均则暴露了经济不平等的问题。因此，全球视角下的家庭资产分析可以揭示国际经济动态，有助于在全球范围内制定更有效的财富管理和经济政策。

研究的意义在于：政策制定的依据：通过对家庭资产的研究，可以为政府和政策制定者提供关于经济福利和社会公平的深入洞察。这有助于制定更加有效的经济政策，以促进财富的公平分配。经济结构分析。。。。。

二、文献综述研究

近年来,利用人工智能技术进行预测研究掀起了新浪潮。监督机器学习方法可以自动分析和挖掘已知矿床与勘探数据之间的复杂关系,已被广泛的应用于矿产预测建模。然而,在矿产潜力评价实践中,矿床数量的有限使得监督机器学习模型面临着巨大挑战,限制了模型的表现与泛化性。在本研究中,李全可、陈国雄等人聚焦于各种半监督机器学习模型(例如半监督随机森林和半监督支持向量机),利用半监督学习机制解决矿床稀缺带来的挑战,并提出一种基于半监督生成对抗网络的半监督深度学习矿产预测建模方法,以实现更准确的矿产潜力评价。。。。。

下面，我们将详细介绍数据预处理步骤以及随机森林模型的构建和评估方法。随机森林模型的应用不仅能够提高预测准确性，还能提供对特征重要性的深入洞察，帮助我们更好地理解各影响因素如何共同作用于家庭资产的变化。。。

三、基础理论和研究

随机森林就是通过集成学习的Bagging思想将多棵树集成的一种算法：它的基本单元就是决策树。随机森林的名称中有两个关键词，一个是“随机”，一个就是“森林”。“森林”很好理解，一棵叫做树，那么成百上千棵就可以叫做森林了，其实这也是随机森林的主要思想--集成思想的体现。。。。。

随机森林的训练过程可以分为以下几个步骤：

（1）随机选择一部分数据样本，构建决策树。

（2）随机选择一部分特征，构建决策树。

（3）重复上述步骤，构建多个决策树。

（4）通过投票的方式，将多个决策树的预测结果合并为最终结果。。。。

四、实证分析

本文数据选取为美国财富网站家庭资产的数据集，其中特征为familynum、consump_total、income_total、debt，响应变量为asset。

首先读取数据集并且展示数据前五行：

数据和代码

数据代码完整报告

df<- read.csv("data_clean.csv")
df

# 显示数据框的前几行
head(df)
str(df)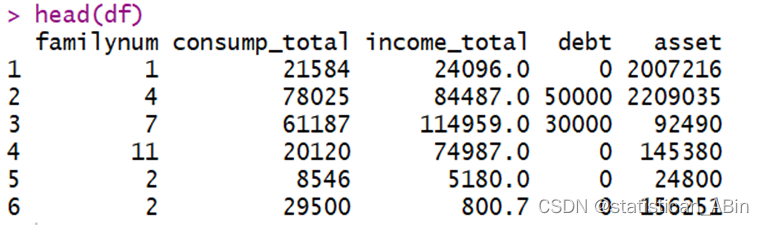

接下来查看数据字符类型：

其中familynum：这是一个整数（int）类型的变量，代表家庭成员的数量。consump_total：是一个数值类型的变量，代表家庭的总消费。 

接下来进行数据缺失值查看：

# 绘制热图
ggplot(missing_df, aes(x = row_id, y = variable, fill = value)) +
  geom_tile() +
  scale_fill_manual(values = c("Missing" = "red", "Not Missing" = "gray")) +
  theme_minimal() +
  labs(x = "Row Number", y = "Variable", fill = "Status", title = "Heatmap of Missing Values")

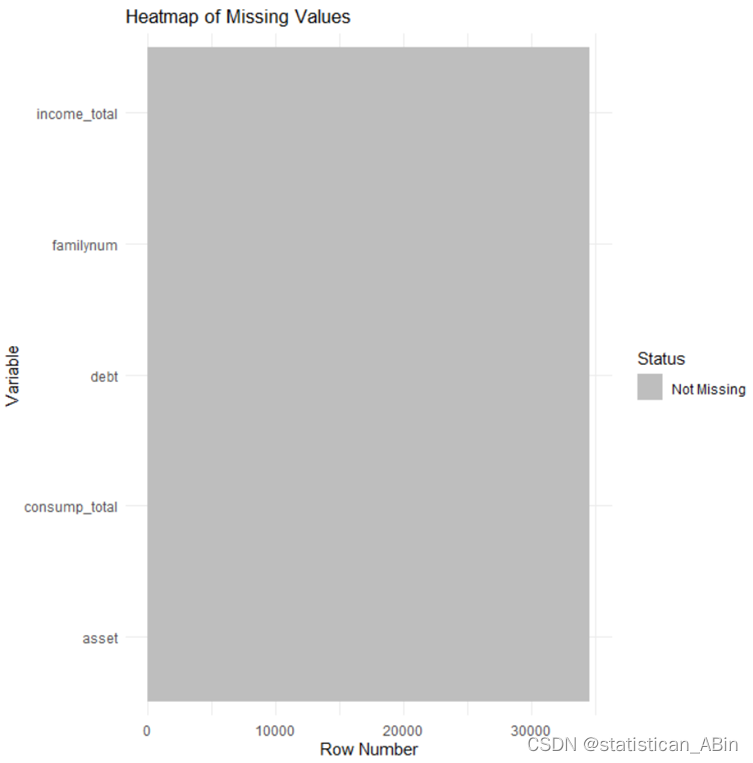
热图中的深色部分表明数据值“不缺失”（Not Missing），而如果存在缺失值，我们通常会看到标记为其他颜色。。。

接下来进行部分数据可视化：

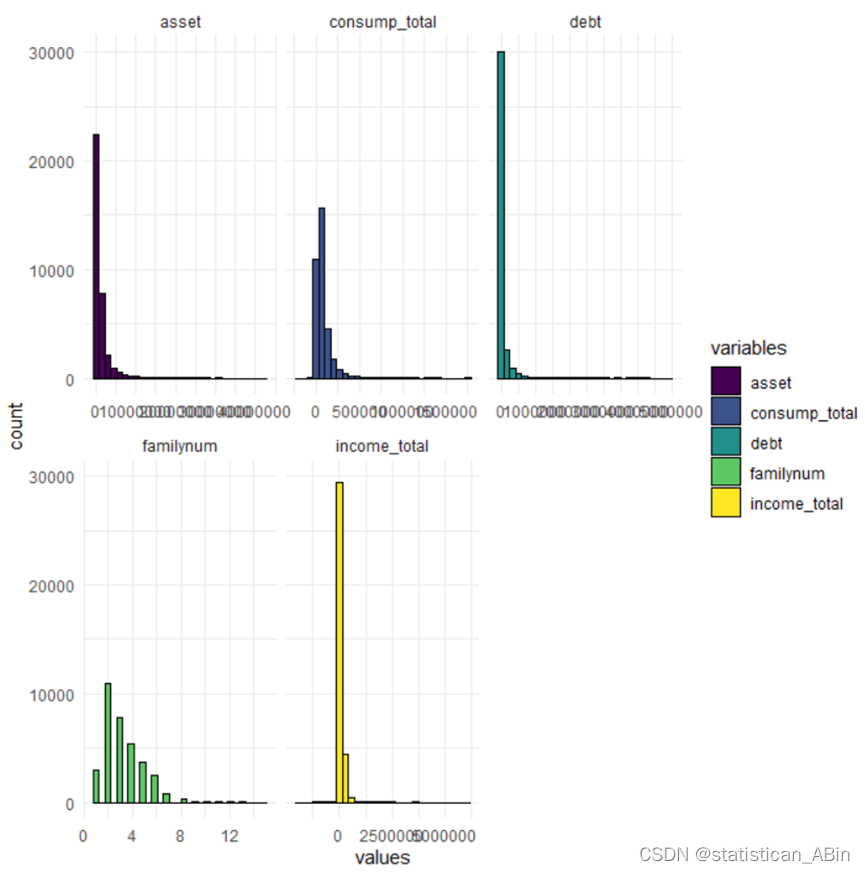
家庭资产（asset）：大多数数据集中在较低的资产值，说明在样本中低资产家庭的数量较多。分布的长尾部分表示有少数家庭拥有很高的资产。总消费消费数据似乎也是右偏的 。。。

box_plots <- df %>%
  pivot_longer(cols = everything(), names_to = "variables", values_to = "values") %>%
  ggplot(aes(x = as.factor(variables), y = values)) +
  geom_boxplot() +
  facet_wrap(~variables, scales = 'free') +
  theme_minimal()
print(box_plots)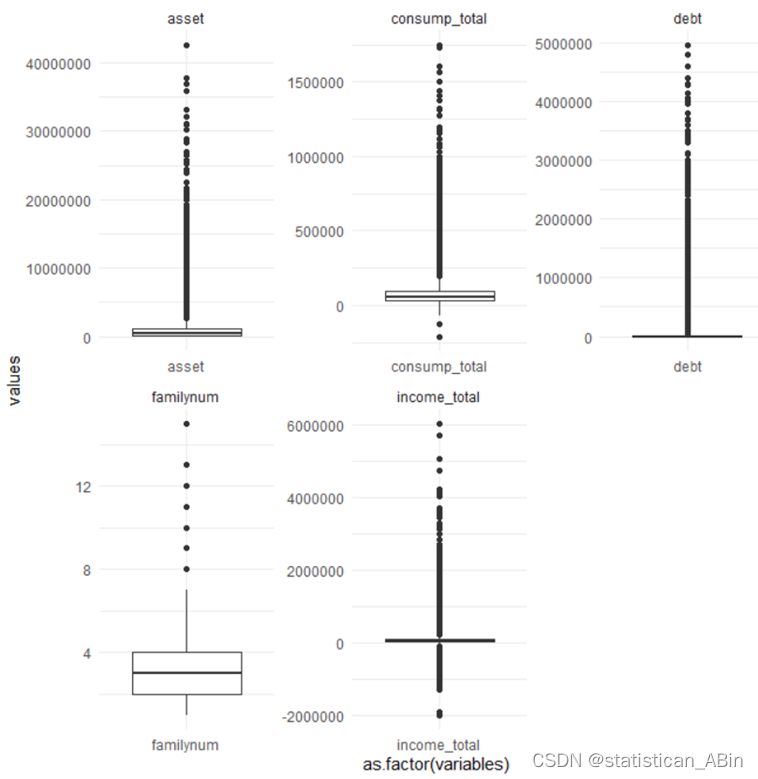

家庭成员数的分布相对均匀，中位数在2左右，异常值分布在较高的家庭成员数，但这些异常值并不极端。总收入的中位数较低，分布范围相对较广，存在一些高收入的异常值。

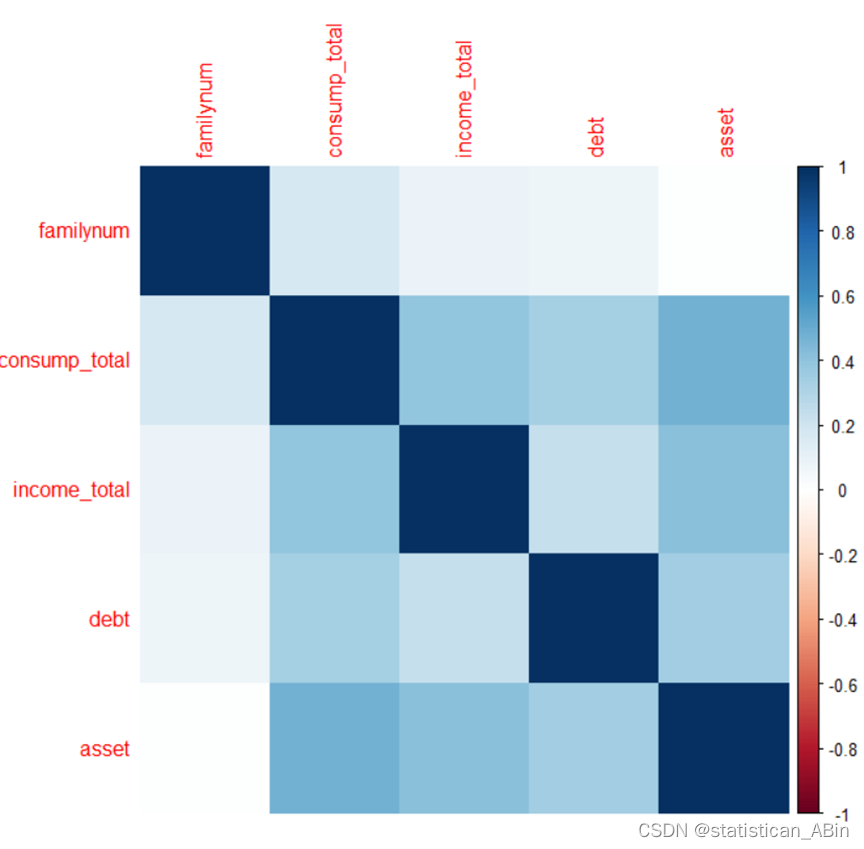 从热力图可知，家庭成员数与其他变量似乎没有显示出很强的相关性。总消费与总收入之间显示出一定的正相关性，这是合理的，因为通常收入水平较高的家庭可能会有更多的消费。。。。

接下来正式进入随机森林建模和预测，这里的训练集和测试集的划分比例为3：7。

# 建立随机森林模型
rf_model <- randomForest(asset ~ ., data = train_data, ntree = 100)
rf_model

从上图可以看得，模型设置了100棵树，并且在每次分裂时尝试了1个变量。 模型中建立了100棵决策树。随机森林是通过结合多棵决策树的预测来提高整体预测准确性和鲁棒性的。平均平方残差约为2.517×10¹²。 

在预测之后对模型进行评价：

表1 随机森林模型预测评价结果

RMSE	Rsquared	MAE
1525606.6201528	0.3679425	792606.7109922

最后可视化一下特征重要性图，在特征中对比一下：

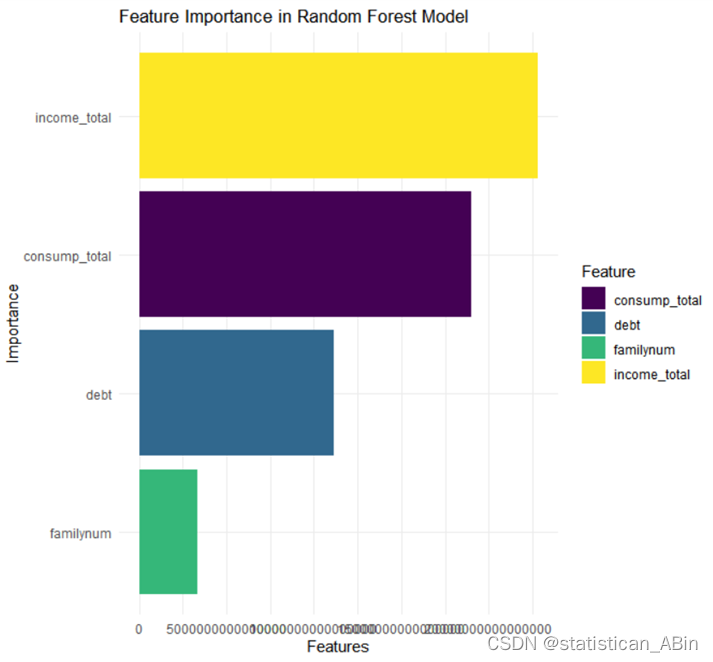
从该图可知，特征按重要性降序排列，具有以下特点：

income_total（总收入）: 这个特征在模型中的重要性最高，表现为最长的黄色条形。这意味着总收入在预测家庭资产方面起着最关键的作用。。。。

五、总结与展望

本次实验通过随机森林回归模型分析了影响家庭资产的几个关键变量得到了一些初步的结论

总收入对家庭资产的预测作出了最大的贡献，这表明收入水平是影响家庭资产积累的一个重要因素。总消费也是家庭资产预测的一个重要变量，但其影响力度低于总收入。债务与家庭资产之间存在一定的相关性，尽管其影响不如收入和消费那么显著。。。。

创作不易，希望大家多点赞关注评论！！！（类似代码或报告定制可以私信）