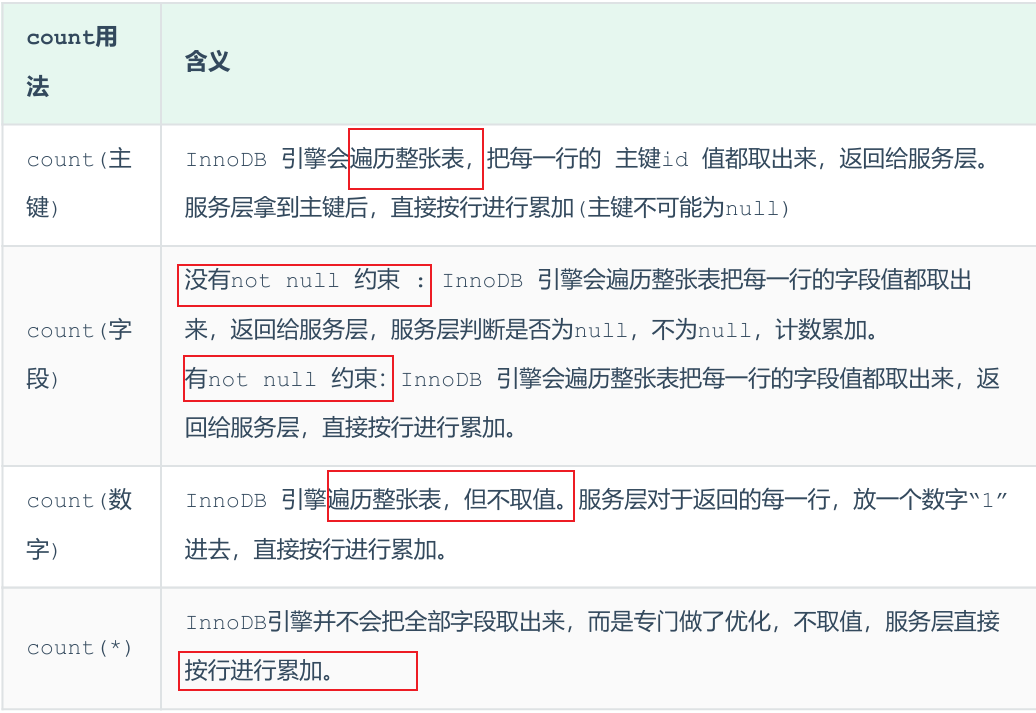
并查集的原理
并查集(Union-Find Set)。可以把每个连通分量看成一个集合,该集合包含了连通分量中的所有点。这些点两两连通(连通性),而具体的连通方式无关紧要,就好比集合中的元素没有先后顺序之分(无序性),只有“属于”和“不属于”的区别(确定性)。在图中,每个点恰好属于一个连通分量,对应到集合表示中,每个元素恰好属于一个集合。换句话说,图的所有连通分量可以用若干个不相交集合来表示。
并查集的精妙之处在于用树来表示集合。例如,若包含点1,2,3,4,5,6的图有3个连通分量{1,3}、{2,5,6}、{4},则需要用3棵树来表示。这3棵树的具体形态无关紧要,只要有一棵树包含1、3两个点,一棵树包含2、5、6这3个点,还有一棵树只包含4这一个点即可。规定每棵树的根结点是这棵树所对应的集合的代表元(representative)。 ——摘自网络
意思就是并查集里的每一个连通分量都是一棵树,属的每个子节点,对应的都是这个树的根,而如果想让这两个连通分量合并我们只需要让一个的代表元,也就是这棵树的树根成为另一棵树的代表元,也就是另一棵树的树根的子节点。这样子这棵树的树根对应的代表元是另一棵树的树根这时,这两个连通分量就合并了。
并查集的操作
1.利用启发式合并
启发式合并的基本原理是每次尝试将较小的集合填入较大的集合,每一个元素维护其所在集合的大小,这时并查集的时间复杂度为。 ——《CCF中学生计算机程序设计·提高篇》
这是实现的代码:
![]()
通俗地讲就是:如果p[x]等于x,说明x本身就是树根,因此返回x;否则返回x的父结点p[x]所在树的树根(代表元)。 ——摘自网络
2.路径压缩技术
我们发现集合中只有代表原是有用的,所以在遍历到集合的其他点时可以让它们变成代表元。在启发式合并的基础上加上路径压缩可以在时间复杂度上进行很大的优化。此时的时间复杂度是, 这里的a(n)是阿克曼函数的反函数,大家可以去查一下阿克曼函数的证明,其实它是一个非原始递归函数,
Ackermann函数定义如下: 若m=0,返回n+1。
若m>0且n=0,返回Ackermann(m-1,1)。
若m>0且n>0,返回Ackermann(m-1,Ackermann(m,n-1))。 ——百度
你可以把它理解为一个不超过4的常数(很快很快),也就是find函数的时间复杂度为。
![]()
这里大家可以看到和上面启发式合并的代码只有一个区别就是递归时当时的
改为了
。也就是把路过的所有点都变成那个点的代表元,也就是那个点所对应的树根。并查集的效率非常高,在平摊意义下,find函数的时间复杂度几乎可以看成是常数(而union显然是常数时间)。
并查集的应用
并查集一般和Kruskal算法结合在一起,用于判定最小生成树,最小瓶颈生成树,最小瓶颈路,或者次小生成树等问题。实现代码如下:
int cmp(const int i, const int j) { return w[i]<w[j]; } //间接排序函数
int find(int x) { return p[x] == x ? x : p[x] = find(p[x]);}//并查集的find
int Kruskal() {
int ans = 0;
for(int i = 0; i < n; i++) p[i] = i; //初始化并查集
for(int i = 0; i < m; i++) r[i] = i; //初始化边序号
sort(r, r+m, cmp); //给边排序
for(int i = 0; i < m; i++) {
int e = r[i]; int x = find(u[e]); int y = find(v[e]);
//找出当前边两个端点所在集合编号
if(x != y) { ans += w[e]; p[x] = y; } //如果在不同集合,合并
}
return ans;