对抗式生成模仿学习（GAIL）

1 预先基础知识

1.1 对抗生成网络（GAN）

1.1.1 基本概念

1.1.2 损失函数

1.1.2.1 固定G，求解令损失函数最大的D

1.1.2.2 固定D，求解令损失函数最小的G

1.2 对抗式生成模仿学习特点

2 对抗式生成模仿学习（GAIL）详细说明

3 参考文献

1 预先基础知识

1.1 对抗生成网络（GAN）

1.1.1 基本概念

在GAN生成对抗网络中，包含两个模型，一个生成模型，一个判别模型。

生成模型：负责生成看起来真实自然，和原始数据相似的实例。
判别模型：负责判断给出的实例是真实的还是人为伪造的。

生成模型努力去欺骗判别模型，判别模型努力不被欺骗，这样两种模型交替优化训练，都得到了提升。

对于辨别器，如果得到的是生成图片辨别器应该输出0，如果是真实的图片应该输出 1，得到误差梯度反向传播来更新参数。对于生成器，首先由生成器生成一张图片，然后输入给判别器判别并的到相应的误差梯度，然后反向传播这些图片梯度成为组成生成器的权重。直观上来说就是：辨别器不得不告诉生成器如何调整从而使它生成的图片变得更加真实。

1.1.2 损失函数

GAN模型的目标函数：

其中，参考GAN的架构图，字母 V是原始GAN论文中指定用来表示该交叉熵的字母，x 表示任意真实数据，z 表示与真实数据相同结构的任意随机数据，G(z)表示在生成器中基于 z 生成的假数据，而D(x)表示判别器在真实数据 x上判断出的结果，D(G(z))表示判别器在假数据 G(z)上判断出的结果，其中 D(x) 与D(G(z))都是样本为“真”的概率，即标签为1的概率。

上式，主要意思是先固定生成器G，从判别器D的角度令损失最大化，紧接着固定D，从生成器G的角度令损失最小化，即可让判别器和生成器在共享损失的情况下实现对抗。其中第一个期望 $\mathbb{E}_{x \sim p_{\text{data}}(x)} \left[ \log D(x) \right]$ 是所有x都是真实数据时(log(D(x)))的期望，第二个期望 $\mathbb{E}_{z \sim p(z)} \left[ \log (1 - D(G(z))) \right]$ 是所有数据都是生成数据时log(1-D(G(z)))的期望。可以看出，在求解最优解的过程中存在两个过程：

固定G，求解令损失函数最大的D
固定D，求解令损失函数最小的G

判别网络是一个2分类，目标是分清真实数据和伪造数据，也就是希望D(x) 趋近于1，D(G(z))趋近于0，这也就体现了对抗的思想。G网络的loss是log(1-D(G(z)))，D的loss是-(log(D(x)))+log(1-D(G(z)))。

1.1.2.1 固定G，求解令损失函数最大的D

判别器D的输入x有两部分：一部分是真实数据，设其分布为 $P_{\text{data}}(x)$ ；另一部分是生成器生成的数据，参考架构图，生成器接收的数据z服从分布P(z)，A输入z经过生成器的计算生成的数据分布设为 $P_{G}(x)$ 。

这两部分这两部分都是判别器D的输入，不同的是，G的输出来自分布 $P_{G}(x)$ ，而真实数据来自分布 $P_{\text{data}}(x)$ ，经过一系列推导后的结果：

可以看出，固定G，将最优的D带入后，此时V（G，D*），实际上是在度量 $P_{\text{data}}(x)$ 和 $P_{G}(x)$ 之间的JS散度，同KL散度一样，他们之间的分布差异越大，JS散度值也越大。换句话说：保持G不变，最大化V(G,D)就等价于计算JS散度。对于判别器来说，尽可能找出生成器生成的数据与真实数据分布之间的差异，这个差异就是JS散度。

1.1.2.2 固定D，求解令损失函数最小的G

对于生成器来说，让生成器生成的数据分布接近真实数据分布。现在第一步已经求出了最优解的D*，代入损失函数：

在最小化JS散度，JS散度越小，分部之间的差异越小，正好印证了第二个原则。

1.2 对抗式生成模仿学习特点

逆强化学习（Inverse Reinforcement Learning, IRL）作为一种典型的模仿学习方法，顾名思义，逆强化学习的学习过程与正常的强化学习利用奖励函数学习策略相反，不利用现有的奖励函数，而是试图学出一个奖励函数，并以之指导基于奖励函数的强化学习过程。IRL可以归结为解决从观察到的最优行为中提取奖励函数（ Reward Function）的问题，这些最优行为也可以表示为专家策略。基于IRL的方法交替地在两个过程中交替：一个阶段是使用示范数据来推断一个隐藏的奖励（Reward）或代价（ Cost）函数，另一个阶段是使用强化学习基于推断的奖励函数来学习一个模仿策略。IRL的基本准则是：IRL选择奖励函数来优化策略，并且使得任何不同于 $\Pi _{E}$ 的动作决策尽可能产生更大损失。

对抗式生成模仿学习（Generative Adversarial Imitation Learning，GAIL）是逆强化学习的一种重要实现方法之一。逆强化学习旨在从专家示范的行为中推断环境的奖励函数或者价值函数，而GAIL是逆强化学习的一种实现方式，它利用了生成对抗网络（GAN）的概念来进行模仿学习。

GAIL的关键点在于：

1）生成对抗网络： GAIL使用生成对抗网络的框架，其中包括生成器和判别器。

2）生成器与判别器：生成器尝试生成与专家示范行为相似的状态-动作对，而判别器则尝试区分专家行为和生成器生成的行为。

3）对抗优化： GAIL使用对抗训练的思想，通过生成器和判别器的对抗优化来使得生成器的输出逼近专家的行为。

GAIL的工作方式使得它在逆强化学习中发挥着重要作用，因为它提供了一种有效的方式来从专家示范中学习环境的奖励结构，以指导智能体的学习行为。通过对抗式生成模仿学习，智能体可以学习并模仿专家的行为，而无需显式地使用环境的奖励信号。

因此，GAIL作为逆强化学习的一种方法，为从专家示范中学习环境的奖励函数或者价值函数提供了一种有效的框架和方法。

2 对抗式生成模仿学习（GAIL）详细说明

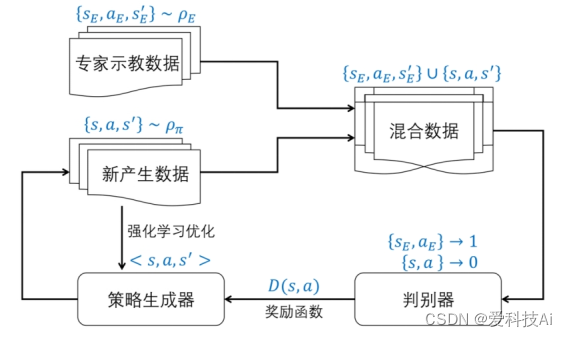
生成式对抗模仿学习的整体优化流程如图所示。通过 GAIL 方法，策略生成器通过生成类似专家示教样本的探索样本，泛化示教样本的概率分布，逼近专家示范行为数据，进而实现模仿专家技能的目的。该过程直接优化采样样本的概率分布，计算代价较小且算法通用性更强，实际模仿效果也更好。

伪代码：

# 初始化策略 π、判别器 D、专家示范数据 D_expert、策略缓冲区 D_policy

函数 GAIL_Training():
    初始化策略 π 的参数
    初始化判别器 D 的参数

    循环 直到收敛 或 达到最大迭代次数:
        # 使用当前策略 π 生成轨迹并存储在策略缓冲区 D_policy 中
        生成 trajectories 使用 π 并存储在 D_policy 中

        # 判别器训练
        循环 discriminator_updates 次数:
            # 从策略缓冲区 D_policy 中采样数据
            采样 (s_policy, a_policy) 从 D_policy 中
            # 从专家示范数据 D_expert 中采样数据
            采样 (s_expert, a_expert) 从 D_expert 中

            # 更新判别器 D
            计算 L_D = -[log(D(s_expert, a_expert)) + log(1 - D(s_policy, a_policy))]
            使用梯度下降法更新判别器参数以最小化 L_D

        # 策略更新
        采样 (s, a, ...) 从 D_policy 中
        计算伪奖励 r = -log(1 - D(s, a))

        # 使用伪奖励 r 更新策略 π
        计算 L_π 使用 PPO 或 其他强化学习方法
        使用梯度下降法更新策略 π 的参数以最大化 L_π

能够表征GAIL流程的主程序如下：

import torch
from torch import nn
import torch.nn.functional as F
from torch.optim import Adam

from .ppo import PPO
from gail_airl_ppo.network import GAILDiscrim


class GAIL(PPO):

    def __init__(self, buffer_exp, state_shape, action_shape, device, seed,
                 gamma=0.995, rollout_length=50000, mix_buffer=1,
                 batch_size=64, lr_actor=3e-4, lr_critic=3e-4, lr_disc=3e-4,
                 units_actor=(64, 64), units_critic=(64, 64),
                 units_disc=(100, 100), epoch_ppo=50, epoch_disc=10,
                 clip_eps=0.2, lambd=0.97, coef_ent=0.0, max_grad_norm=10.0):
        super().__init__(
            state_shape, action_shape, device, seed, gamma, rollout_length,
            mix_buffer, lr_actor, lr_critic, units_actor, units_critic,
            epoch_ppo, clip_eps, lambd, coef_ent, max_grad_norm
        )

        # Expert's buffer.
        self.buffer_exp = buffer_exp

        # Discriminator.
        self.disc = GAILDiscrim(
            state_shape=state_shape,
            action_shape=action_shape,
            hidden_units=units_disc,
            hidden_activation=nn.Tanh()
        ).to(device)

        self.learning_steps_disc = 0
        self.optim_disc = Adam(self.disc.parameters(), lr=lr_disc)
        self.batch_size = batch_size
        self.epoch_disc = epoch_disc

    def update(self, writer):
        self.learning_steps += 1

        for _ in range(self.epoch_disc):
            self.learning_steps_disc += 1

            # Samples from current policy's trajectories.
            states, actions = self.buffer.sample(self.batch_size)[:2]
            # Samples from expert's demonstrations.
            states_exp, actions_exp = \
                self.buffer_exp.sample(self.batch_size)[:2]
            # Update discriminator.
            self.update_disc(states, actions, states_exp, actions_exp, writer)

        # We don't use reward signals here,
        states, actions, _, dones, log_pis, next_states = self.buffer.get()

        # Calculate rewards.
        rewards = self.disc.calculate_reward(states, actions)

        # Update PPO using estimated rewards.
        self.update_ppo(
            states, actions, rewards, dones, log_pis, next_states, writer)

    def update_disc(self, states, actions, states_exp, actions_exp, writer):
        # Output of discriminator is (-inf, inf), not [0, 1].
        logits_pi = self.disc(states, actions)
        logits_exp = self.disc(states_exp, actions_exp)

        # Discriminator is to maximize E_{\pi} [log(1 - D)] + E_{exp} [log(D)].
        loss_pi = -F.logsigmoid(-logits_pi).mean()
        loss_exp = -F.logsigmoid(logits_exp).mean()
        loss_disc = loss_pi + loss_exp

        self.optim_disc.zero_grad()
        loss_disc.backward()
        self.optim_disc.step()

        if self.learning_steps_disc % self.epoch_disc == 0:
            writer.add_scalar(
                'loss/disc', loss_disc.item(), self.learning_steps)

            # Discriminator's accuracies.
            with torch.no_grad():
                acc_pi = (logits_pi < 0).float().mean().item()
                acc_exp = (logits_exp > 0).float().mean().item()
            writer.add_scalar('stats/acc_pi', acc_pi, self.learning_steps)
            writer.add_scalar('stats/acc_exp', acc_exp, self.learning_steps)