【摘要】问答(Q&A)平台通常推荐问答对来满足用户的知识获取需求,这与仅推荐单个项目的传统推荐不同。这使得用户行为更加复杂,并为Q&A推荐带来了两个挑战,包括:协作信息纠缠,即用户反馈受问题或答案的影响;以及语义信息纠缠,其中问题与其相应的答案相关联,不同问答对之间也存在相关性。传统的推荐方法将问答对视为一个整体或仅将答案视为单个项目,忽略了这两个挑战,无法有效地模拟用户兴趣。为了应对这些挑战,我们引入了问答图形协同过滤 (QAGCF),这是一个图神经网络模型,创建了协作视图和语义视图的独立图,以解开问答对中的信息。协作视图分离问题和答案以单独建模协作信息,而语义视图捕获问答对内部以及问答对之间的语义信息。这些视图进一步合并到全局图中,以整合协作和语义信息。多项式基础图滤波器用于解决全局图的高异质性问题。此外,对比学习在训练期间用于获得稳健的嵌入。在工业和公共数据集上的大量实验表明,QAGCF始终优于基线并达到了最先进的结果。

原文：QAGCF: Graph Collaborative Filtering for Q&A Recommendation
地址：https://arxiv.org/html/2406.04828v1
代码：未知
出版：未知
机构: 中国人民大学、腾讯

1 研究问题

本文研究的核心问题是: 如何设计图神经网络模型,以有效解决问答推荐中存在的协作信息纠缠和语义信息纠缠问题。
::: block-1
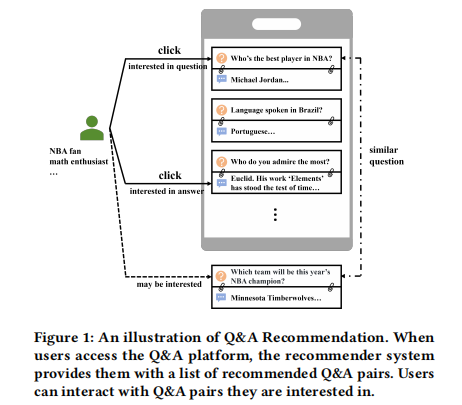
假设用户小明在知乎上浏览问答内容。他看到了一个问题"NBA历史上最伟大的球员是谁?"并点击了进去,是因为他本身很喜欢篮球相关的话题。但是当他浏览回答时,他被一个答案中提到的另一个问题"欧几里得写了哪些著作?"吸引,又点击进入了这个数学史相关的问题。这个例子体现了协作信息纠缠(用户点击行为受问题和答案双重影响)和语义信息纠缠(不同问答对之间存在相关性)的现象。
:::

本文研究问题的特点和现有方法面临的挑战主要体现在以下几个方面:

• 用户反馈受问题和答案的双重影响,协作信息纠缠在一起。将问答对作为一个整体或只关注答案,无法区分问题和答案各自承载的协作信息。
• 问答对内部,问题和答案之间存在语义相似性;不同问答对之间,问题与问题、答案与答案也存在相似性,语义信息纠缠在一起。将问答对作为一个整体或只关注答案,无法区分问答对内部和问答对之间蕴含的语义信息。
• 现有的推荐算法主要针对item序列,很少有研究关注Q&A推荐这类以问答对形式呈现的特殊推荐场景。

针对这些挑战,本文提出了一种基于图神经网络、能解纠协作信息和语义信息的"问答图协同过滤"(QAGCF)方法:

::: block-1
QAGCF巧妙地构建了两个视图来解开问答对中纠缠的信息:协作视图和语义视图。在协作视图中,它构建了用户-问题二部图和用户-答案二部图,分别建模用户与问题、用户与答案之间的协作关系,实现了协作信息的解纠。在语义视图中,一方面它在问题和答案之间建立了加权边,另一方面它在不同的问题之间也建立了语义相似边,实现了语义信息在问答对内部和问答对之间的解纠。这种双视图、多图谱的建模范式犹如"孪生子"探案,从不同角度审视案情,最终拼凑出真相。接下来,QAGCF将协作视图和语义视图巧妙地融合到一个全局异质图中,利用多项式图滤波器处理其中的高频噪声和低频平滑信号,提取出最具判别力的中频特征。同时,它还引入了对比学习范式,通过随机扰动等数据增强手段,进一步提升了特征表示的鲁棒性。可以说,QAGCF犹如一位睿智的侦探,以简洁而独特的视角抽丝剥茧,最终还原了Q&A推荐中协作信息和语义信息的本来面目。
:::

2 研究方法

本文提出了一种新颖的基于图神经网络的问答推荐模型QAGCF。它通过创建协作视图和语义视图的方式来解耦问答对中的协同信息和语义信息。接下来，我们将详细阐述该模型的每个组成部分。

2.1 问答对信息解耦

我们首先从协作视图和语义视图构建图，以分别解决协同信息纠缠和语义信息纠缠的挑战。

在协作视图中，我们将问答对解耦为问题和回答两部分，分别构建用户-问题二部图（U-Q图）和用户-回答二部图（U-A图），以探索用户与问题、用户与回答之间的协同关系。举个例子，一个NBA球迷看到一个问题"谁是NBA最好的球员？"会很感兴趣，可能会点击查看；而一个数学爱好者看到回答中提到"欧几里得，他的著作《几何原本》…"也会点击查看。这体现了用户的点击行为受问题和回答两个因素的影响。U-Q图和U-A图对应的邻接矩阵分别为：

$$A_{uq}=\left[\begin{array}{cc}0& X\\ X^{\top }& 0\end{array}\right],A_{ua}=\left[\begin{array}{cc}0& Y\\ Y^{\top }& 0\end{array}\right]$$

其中$A_{uq}\in {\mathbb{R}}^{(M+N)\times (M+N)}$，$A_{ua}\in {\mathbb{R}}^{(M+O)\times (M+O)}$。$M$、$N$、$O$分别表示用户、问题和回答的数量。

在语义视图中，我们建立问题-回答图（Q-A图）和问题-问题图（Q-Q图）以捕获问答对内部以及不同问答对之间的语义信息。在Q-A图中，我们基于每个回答和问题之间的从属关系来构建。与协同信息不同，语义信息需要对回答和问题之间的相关性进行建模。我们构建一个相关矩阵$C\in {\mathbb{R}}^{N\times O}$，其中每个元素表示问题和回答之间的归一化余弦相似度：

$$C_{i,j}=\{\begin{array}{ll}(\text{cos}(e_i^q,e_j^a)+1)/2,& \text{if}{Z}_{i,j}=1\\ 0,& \text{otherwise}\end{array}$$

其中$e_i^q\in {\mathbb{R}}^d$和$e_j^a\in {\mathbb{R}}^d$分别表示问题$q_i$和回答$a_j$的嵌入表示，$d$为嵌入维度。

在Q-Q图中，我们通过问题之间的相似性来建立联系。具体来说，我们计算问题之间的成对相似度，当相似度较高时，在问题之间建立语义边。我们基于余弦相似度构建问题-问题相似度矩阵$S\in {\mathbb{R}}^{N\times N}$：

$$S_{i,j}=\text{cos}(e_i^q,e_j^q)$$

其中$e_i^q$和$e_j^q$分别表示问题$q_i$和$q_j$的嵌入表示。

然后，我们在完全连接的Q-Q图上保留具有较高相似度的边，同时删除具有较低相似度的边，以获得Q-Q图的邻接矩阵$A_{qq}$：

$${\mathbf{A}}_{qq}^{i,j}=\{\begin{array}{ll}1,& \text{if}i\ne j\text{and}{S}_{i,j}\in \text{top-n}({\mathbf{S}}_i)\\ 0,& \text{otherwise}\end{array}$$

其中函数$\text{top-n}(\cdot )$返回相似度矩阵$S$第$i$行$S_i$的前$n$个值，$n$是一个超参数，设置为$\mu N$，其中$\mu$表示选择比例，控制Q-Q图的稀疏度。

最后，我们将协作视图和语义视图合并到一个全局图中，以整合协同信息和语义信息。全局图的邻接矩阵定义为：

$$\mathbf{A}=\left[\begin{array}{ccc}0& \mathbf{X}& \mathbf{Y}\\ {\mathbf{X}}^{\top }& {\mathbf{A}}_{qq}& \mathbf{C}\\ {\mathbf{Y}}^{\top }& {\mathbf{C}}^{\top }& 0\end{array}\right]$$

其中$\mathbf{A}\in {\mathbb{R}}^{(M+N+O)\times (M+N+O)}$。需要注意的是，我们直接使用Q-A图的相关矩阵$C$而不是从属矩阵$Z$来嵌入相关信息，这使得后续处理更加方便。为了确保训练的稳定性，我们采用其归一化形式：

$$\hat{\mathbf{A}}={\mathbf{D}}^{-\frac{1}{2}}\mathbf{A}{\mathbf{D}}^{-\frac{1}{2}}$$

其中$\mathbf{D}\in {\mathbb{R}}^{(M+N+O)\times (M+N+O)}$是一个对角矩阵，每个条目$D_{ii}$表示$\mathbf{A}$第$i$行中非零条目的数量。

2.2 多项式图滤波

由于全局图包含不同类型的节点和边，导致其具有很强的异质性。现有的图神经网络方法如LightGCN主要关注低频信息，使其更适合于同质场景。然而，最近的研究强调了高频信息在有效处理异质图复杂性方面的重要性。

为了从中频信号中分解出高频和低频信号并单独对其进行建模，我们采用Jacobi多项式基$P_k^{\alpha ,\beta }(x)$作为带阻滤波器，其中$k$是多项式的阶数，$\alpha$和$\beta$是塑造多项式和权函数的参数。第$k$层捕获高频和低频信号的带阻嵌入基于$k$阶Jacobi多项式基计算：

$${\mathbf{E}}_{\text{band-stop}}^{(k)}=P_k^{\alpha ,\beta }(\hat{\mathbf{A}}){\mathbf{E}}^{(0)}$$

其中${\mathbf{E}}_{\text{band-stop}}^{(k)}\in {\mathbb{R}}^{(M+N+O)\times d}$。对于捕获中频信号的带通嵌入，我们从第$k$层的原始信号中减去它：

$${\mathbf{E}}_{\text{band-pass}}^{(k)}=\gamma {\mathbf{E}}^{(0)}-{\mathbf{E}}_{\text{band-stop}}^{(k)}$$

其中$\gamma$是控制中频信号影响的系数。基于公式(7)和(8)，我们可以得到第$k$层的嵌入：

$${\mathbf{E}}^{(k)}=[{\mathbf{E}}_{k,\text{band-stop}};{\mathbf{E}}_{k,\text{band-pass}}]$$

其中${\mathbf{E}}^{(k)}\in {\mathbb{R}}^{(M+N+O)\times 2d}$。最后，经过$K$层后，我们通过以下方式获得用于推荐的最终嵌入：

$$\mathbf{E}=\frac{1}{K}\sum _{k=1}^K{\mathbf{E}}^{(k)}$$

2.3 对比学习优化

我们引入对比学习损失来学习训练过程中更鲁棒的嵌入表示。具体来说，我们对第$k$层($k>0$)节点$i$的带阻嵌入${\mathbf{e}}_{i,\text{band-stop}}^{(k)}$实施基于噪声的嵌入增强：

$${\mathbf{e}}_{i,\text{band-stop}}^{(k{)}^{\prime }}={\mathbf{e}}_{i,\text{band-stop}}^{(k)}+\Delta$$

其中添加的噪声向量$\Delta \in {\mathbb{R}}^d$需要满足：

$$\Delta =\omega \odot \text{sign}({\mathbf{e}}_{i,\text{band-stop}}^{(k)}),\omega \in {\mathbb{R}}^d\sim U(0,1)$$

这迫使噪声不会导致较大的偏差。然后根据公式(8)，第$k$层节点$i$的增强带通嵌入为：

$${\mathbf{e}}_{i,\text{band-pass}}^{(k{)}^{\prime }}=\gamma {\mathbf{e}}_i^{(0)}-{\mathbf{e}}_{i,\text{band-stop}}^{(k{)}^{\prime }}-\Delta$$

然后，基于公式(9)和(10)，我们可以得到第$k$层节点$i$的增强嵌入${\mathbf{e}}_i^{(k{)}^{\prime }}=[{\mathbf{e}}_{i,\text{band-stop}}^{(k{)}^{\prime }};{\mathbf{e}}_{i,\text{band-pass}}^{(k{)}^{\prime }}]$以及最终嵌入${\mathbf{e}}_i^{\prime }$。接下来，我们定义跨层对比损失如下：

$$\begin{array}{rl}{\mathcal{L}}_C=& -\sum _{i\in \mathcal{U}}\log \frac{\exp ({\mathbf{e}}_i^{\prime \top }{\mathbf{e}}_i^{(l{)}^{\prime }}/\tau )}{{\sum }_{j\in {\mathcal{U}}_{\text{neg}}}\exp ({\mathbf{e}}_i^{\prime \top }{\mathbf{e}}_j^{(l{)}^{\prime }}/\tau )}\\ & -\sum _{i\in \mathcal{Q}}\log \frac{\exp ({\mathbf{e}}_i^{\prime \top }{\mathbf{e}}_i^{(l{)}^{\prime }}/\tau )}{{\sum }_{j\in {\mathcal{Q}}_{\text{neg}}}\exp ({\mathbf{e}}_i^{\prime \top }{\mathbf{e}}_j^{(l{)}^{\prime }}/\tau )}\\ & -\sum _{i\in \mathcal{A}}\log \frac{\exp ({\mathbf{e}}_i^{\prime \top }{\mathbf{e}}_i^{(l{)}^{\prime }}/\tau )}{{\sum }_{j\in {\mathcal{A}}_{\text{neg}}}\exp ({\mathbf{e}}_i^{\prime \top }{\mathbf{e}}_j^{(l{)}^{\prime }}/\tau )}\end{array}$$

其中$\tau$是温度，$l$表示与最终嵌入进行对比的层，在我们的模型中设置为1。${\mathcal{U}}_{\text{neg}}$、${\mathcal{A}}_{\text{neg}}$、${\mathcal{Q}}_{\text{neg}}$是随机采样的批内负样本。${\mathcal{L}}_C^u$、${\mathcal{L}}_C^q$和${\mathcal{L}}_C^a$分别是用户、问题和回答的对比损失。总的对比损失计算为：

$${\mathcal{L}}_C={\mathcal{L}}_C^u+{\mathcal{L}}_C^q+{\mathcal{L}}_C^a$$

这种对比损失的目的是使不同层中同一节点的表示更接近，同时使不同层中不同节点的表示更远离，从而缓解由过多层引起的潜在过度平滑问题，并学习更鲁棒的表示。

2.4 模型训练与复杂度

首先，我们根据增强嵌入${\mathbf{e}}_i^{\prime }$计算用户-问题和用户-回答的内积，然后通过加权求和得到最终预测：

$${\hat{y}}_{u,q,a}={\mathbf{e}}_u^{\prime \top }{\mathbf{e}}_a^{\prime }+{\lambda }_1{\mathbf{e}}_u^{\prime \top }{\mathbf{e}}_q^{\prime }$$

其中${\lambda }_1$是控制问题影响的系数。然后采用广泛使用的贝叶斯个性化排序(BPR)损失：

$${\mathcal{L}}_{BPR}=\sum _{(u,⟨q,a⟩,⟨q^{\prime },a^{\prime }⟩)\in \mathcal{O}}-\ln \sigma ({\hat{y}}_{u,q,a}-{\hat{y}}_{u,q^{\prime },a^{\prime }})$$

其中$\sigma (\cdot )$是sigmoid函数，$\mathcal{O}=\{(u,⟨q,a⟩,⟨q^{\prime },a^{\prime }⟩)|X_{uq}=1,Y_{ua}=1,Z_{qa}=1,X_{u{q}^{\prime }}=0,Y_{u{a}^{\prime }}=0,Z_{q^{\prime }{a}^{\prime }}=1\}$表示训练数据，$⟨q^{\prime },a^{\prime }⟩$表示用户$u$未交互过的采样对。

最终损失$\mathcal{L}$包括BPR损失${\mathcal{L}}_{BPR}$和对比损失${\mathcal{L}}_C$：

$$\mathcal{L}={\mathcal{L}}_{BPR}+{\lambda }_2{\mathcal{L}}_C+{\lambda }_3\Vert \Theta {\Vert }_2^2$$

其中${\lambda }_2$和${\lambda }_3$是控制对比损失和$L_2$正则化影响的超参数，$\Theta$是我们模型的参数。

关于空间复杂度，QAGCF的参数只包括三组嵌入：${\mathbf{E}}_U^{(0)}$、${\mathbf{E}}_Q^{(0)}$、${\mathbf{E}}_A^{(0)}$。QAGCF的总空间复杂度为$O((M+N+O)d)$。

关于时间复杂度，QAGCF的计算成本主要来自Q-A相关矩阵计算、Q-Q图构建、三部图学习和对比学习。QAGCF中Q-A相关矩阵和Q-Q图构建的时间复杂度为$O((N+O+\mu N\log (N))Nds)$，其中$\mu$为定义的选择比例。图学习的时间复杂度为$O((|E_{UQ}|+|E_{UA}|+|E_{QA}|+\mu N^2)Kds\frac{|E_{UA}|}{B})$，其中$|E_{UQ}|$、$|E_{UA}|$、$|E_{QA}|$分别是U-Q图、U-A图、Q-A图中的边数，$K$是传播层数，$s$是epoch数，$B$是批量大小。计算对比损失的时间复杂度为$O(B^{2}d)$。

通过以上详细阐述，我们清晰地介绍了QAGCF的研究方法。该方法巧妙地解决了问答对推荐中存在的协同信息纠缠和语义信息纠缠的挑战，并通过对比学习学到更鲁棒的节点表示，在问答推荐任务上取得了优异的效果。

4 实验

4.1 实验场景介绍

本文提出了一个新颖的基于图神经网络的问答推荐模型QAGCF,通过多视图方法解纠缠协同信息和语义信息。论文实验的核心是验证QAGCF相比现有模型在推荐准确性上的优势,以及分析其内部机制。

4.2 实验设置

• Datasets: 在两个问答社区数据集ZhihuRec和Commercial上进行实验。ZhihuRec包含79750个用户、126个问题和31025个答案,共265971个交互。Commercial包含40204个用户、31710个问题和101056个答案,共953212个交互。
• Baselines: 实验比较了四类基准模型:Non-GNN类(BPRMF、NeuMF)、GNN类(NGCF、LightGCL、HMLET、LightGCN)、GNN+多项式图滤波器类(JGCF及其变体)、GNN+对比学习类(SGL、SimGCL、XSimGCL)
• Evaluation Metrics: 采用Top-K推荐常用的Recall@10、MRR@10、NDCG@10、Hit@10和Precision@10五个指标
• Implementation details: 采用RecBole-GNN框架实现QAGCF和所有基线,优化器为Adam,Batch size固定为2048,嵌入维度为64,每10个epoch在验证集上测试,Early stopping耐心为10个epoch

4.3 实验结果

4.3.1 实验一、QAGCF与基线模型的整体性能对比

目的: 验证QAGCF在Top-K推荐任务上的性能优势
涉及图表: 表2
实验细节概述: 在ZhihuRec和Commercial两个数据集上,评估QAGCF与多个基准模型的性能对比情况
结果:

• 基于GNN的方法普遍优于传统的BPRMF等,因为它们能编码图的高阶信息
• 基于多项式图滤波器的JGCF性能优于LightGCN等,说明捕获中高频信息的重要性
• 基于对比学习的XSimGCL在大多baseline中效果最佳,但仍不如QAGCF
• QAGCF始终优于所有baseline,因为它深入挖掘了用户、问题、回答间错综复杂的协同和语义关系,并结合多项式图滤波和对比学习,学到更有效的节点表征

4.3.2 实验二、QAGCF关键组件的消融研究

目的: 评估QAGCF关键组件(图构建、多项式图滤波器、对比学习)对性能的影响
涉及图表: 表3
实验细节概述: 逐个移除QAGCF的关键模块,观察性能变化
结果:

• 分别构建U-A图、U-A+U-Q图的性能逐步提升,但不及全图,说明构建协同视图和语义视图的合理性
• 移除多项式图滤波器,改用LightGCN训练,导致性能显著下降。说明多项式图滤波器更适合处理异质图
• 去掉对比学习损失,性能大幅下降,说明对比学习能学到更鲁棒的嵌入

4.3.3 实验三、QAGCF详细实证分析

目的: 进一步分析QAGCF内部机制,包括协同信息解纠缠效果、图构建方式对比以及超参数影响
涉及图表: 图5-9
实验细节概述: 在ZhihuRec上进行一系列分析实验
结果:

• 协同信息解纠缠: 分别计算测试集每个用户-问题和用户-答案交互的内积比值,覆盖了从很小到很大的全范围,说明通过分别构建U-Q和U-A图,成功解纠缠了用户对问题和答案的偏好差异
• 图构建方式: 将答案嵌入直接加到问题上作为单个节点QAGCF_U(A+Q),性能差于分别构建4个图的QAGCF,突显了协同视图和语义视图构建的重要性
• 超参数影响:
  • Q-Q图构建的μ: 最优值1e-4,导致Q-Q图稀疏度99.99%。过大或过小的μ均降低性能
  • 多项式滤波器的α、β、γ: 最优值α=1.0, β=1.5, γ=0.1。β影响最大,α过大可能过平滑,γ适当抑制中频有利于学习
  • 对比学习的λ2、ω、τ: 最优值λ2=0.1, ω=0.2, τ=0.2。对λ2和τ较敏感,过大过小均降低性能
  • 预测的λ1: 最优值0.1,说明预测更多地受答案嵌入影响

4 总结后记

本论文针对Question and Answer (Q&A)平台的推荐任务,提出了一种新颖的图神经网络模型QAGCF。QAGCF采用多视图方法,从协同视图和语义视图分别构建用户-问题、用户-答案二部图以及问题-答案、问题-问题图,以解开问题-答案对的协同信息和语义信息。同时,QAGCF利用多项式图滤波器有效处理全局图的高度异质性,并引入对比学习目标学习更鲁棒的节点表征。实验结果表明,QAGCF在准确率上一致地超越了现有模型,为增强Q&A平台的用户体验提供了有前景的方向。
::: block-2
疑惑和想法：

1. 除了问题-答案对,是否可以纳入更多元信息(如问题的分类标签)构建更全面的异质图?这对推荐性能会有何影响?
2. 能否将QAGCF与知识图谱等外部知识相结合,以更好地建模问题和答案之间的语义关系?
3. 用户行为模式在不同类型的问题(如事实类、观点类)上可能有所差异,是否可以设计基于问题类型的个性化推荐策略?
   :::
   ::: block-2
   可借鉴的方法点：
4. 采用多视图异质图建模的思想可以推广到其他具有多元关系的推荐场景,如电商平台的用户-商品-店铺关系等。
5. 利用多项式图滤波器处理图的高度异质性的方法值得借鉴,可应用于其他任务的异质图学习中。
6. 将对比学习应用于图神经网络的思路可以广泛应用,以提高节点表征学习的鲁棒性和泛化性能。
   :::