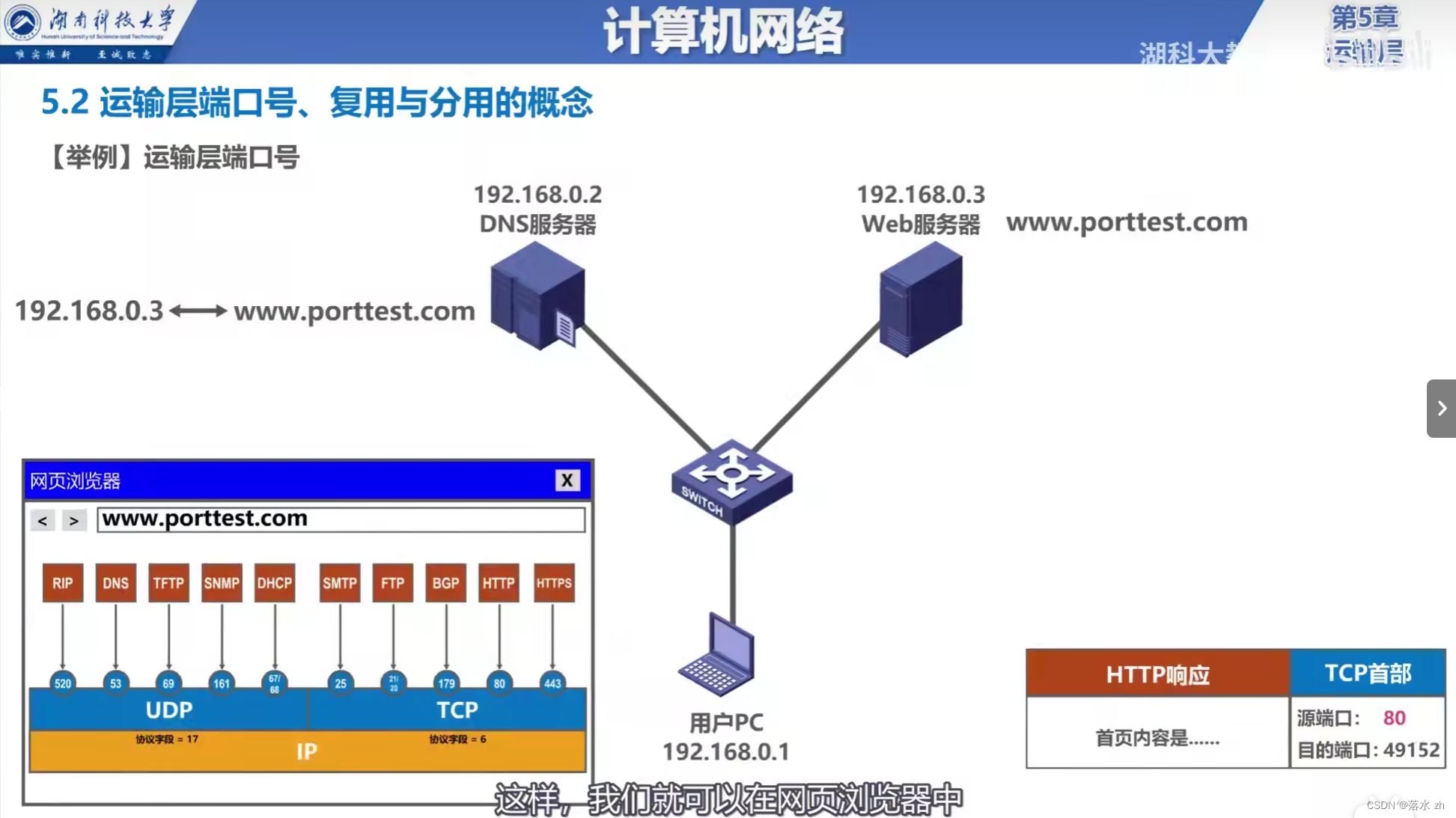
1、RC滤波器
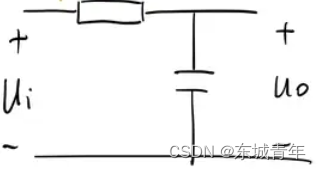
电容容抗公式
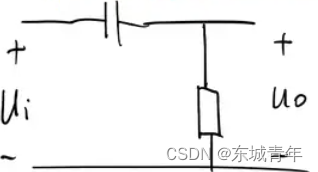
宏观分析:不管是高通还是低通滤波电路,说白了就是一个电容和一个电阻构成了一个分压电路,区别在于电容位置不同。低通滤波电阻在前电容在后,信号频率越高,容抗越小,相应的电容上分压越小,所以频率越高越不容易传递到后端。高通滤波电容在前电阻在后,因此信号频率越高电容上分压越小,那么电阻上的分压就越大,这就构成了高通滤波器。
微观分析:对于低通滤波电路,电源通电后,电子从电源负极流到电容,如果电源是高频信号,由于电容充放电较慢(无法跟随高频信号突变,只能平滑过渡),所以大部分电子都跑到电阻那端去了,所以电容两端电压很小,所以对于高频信号电容分压小,低频信号电容分压大,这就构成了低通滤波器。对于高通滤波电路,电源通电后,电子从电源负极流过电阻再流到电容,如果电源是高频信号,由于电容充放电较慢(无法跟随高频信号突变,只能平滑过渡),所以大部分电子堆积在电阻两端,所以电阻电压很大,这就构成了高通滤波器。
2、RC低通滤波器截止频率公式推导
2.1 一阶低通滤波器

一阶RC滤波器如上图所示,电阻R串联电容C,输入电压记为,输出电压记为
,电容容抗公式为
,根据串联分压,列出传递函数:其中j是代表复数的概念,电容器为无功元件,本身不消耗功率,在频率为
的交流电作用下将会出现电流超前电压90°的情况,因此用复数准确地表示出这种相位关系。
由复数计算,分子分母同乘,则可得到
,计算该复数的模,则有,
复数的模代表了电压增益,当电压增益下降到倍时,此时的频率即为截止频率,记为
,那么就有,
,化简可得,
,求得截止频率
2.2 二阶低通滤波器
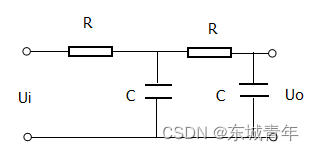
二阶RC滤波器如上图所示,可见由两个一阶电路构成。第一个一阶电路的电阻记为,电容记为
;第二个一阶电路的电阻记为
,电容记为
;输入电压记为
,输出电压记为
,电容容抗公式为
(这里便于分析,取电阻
,电容
)。
二阶电路分析比一阶较为繁琐一点,不过原理还是一样,其中代表
与
的并联等效电阻即
,所以二阶低通滤波器传递函数如下:
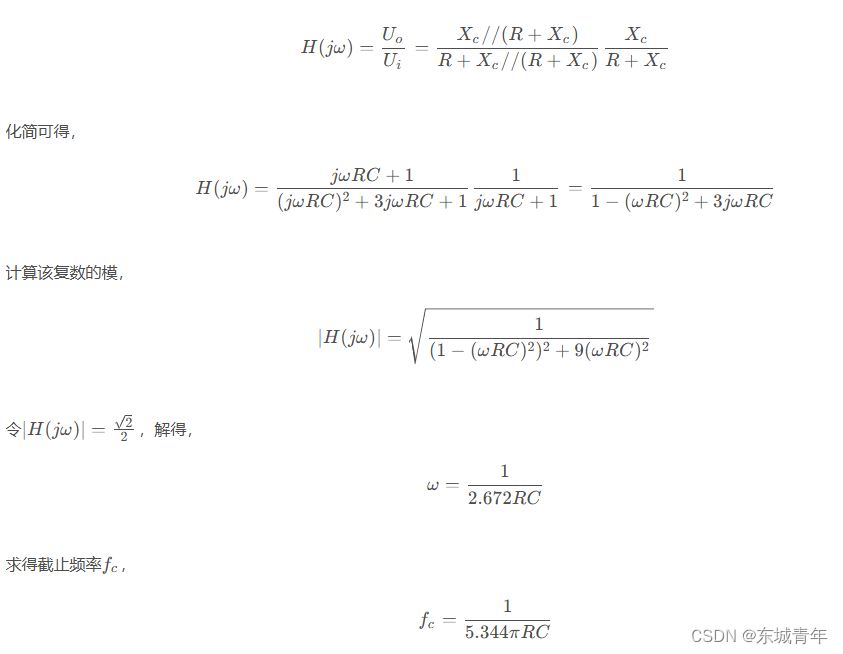
用一个电阻和电容制作高通滤波器与低通滤波器
RC滤波器(低通/高通)
RC低通滤波器截止频率公式推导