参考官方题解2786. 访问数组中的位置使分数最大 - 力扣（LeetCode）

问题描述

给定一个下标从 0 开始的整数数组 nums 和一个正整数 x。你一开始在数组的第 0 个位置，你可以移动到满足 i < j 的任意位置 j。如果你访问的位置 i，你可以获得分数 nums[i]。如果从位置 i 移动到位置 j 且 nums[i] 和 nums[j] 的奇偶性不同，那么你将失去分数 x。请返回你能得到的最大得分之和。

动态规划思想

我们需要用动态规划来解决这个问题，通过维护一个状态数组来记录在不同奇偶性下的最大得分。具体地：

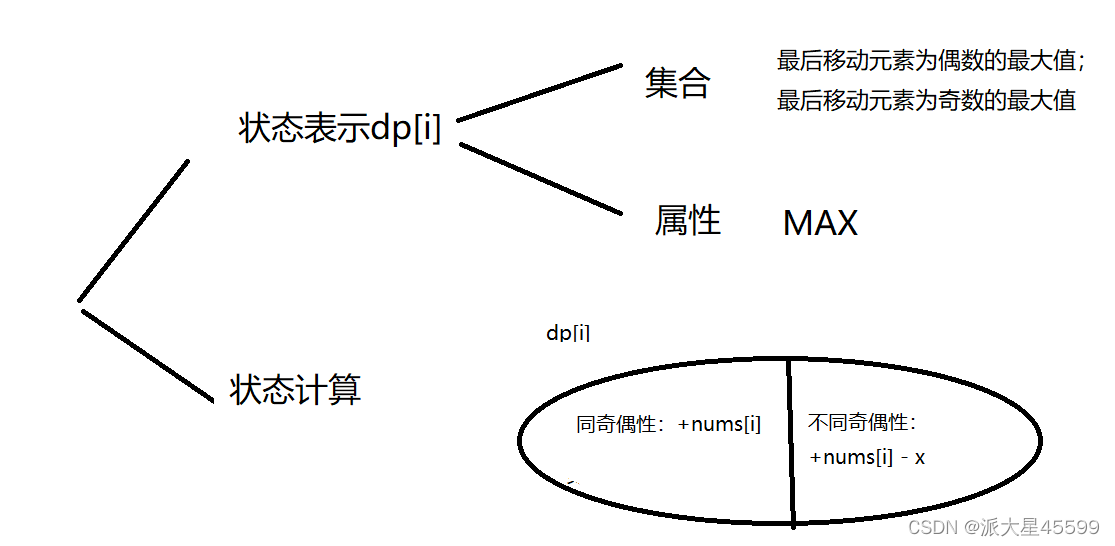
1. 状态定义：

   • dp[0] 表示当前最后一个元素为偶数时的最大得分。

   • dp[1] 表示当前最后一个元素为奇数时的最大得分。

2. 状态初始化：

   • 初始情况下，你在位置 0，所以得分为 nums[0]。

   • 根据 nums[0] 的奇偶性，初始化对应的 dp 值。

3. 状态转移： 对于数组中的每一个元素 nums[i]，计算当前元素为奇数或偶数的情况下的最大得分。

   • 如果 nums[i] 是偶数，parity = 0；

   • 如果 nums[i] 是奇数，parity = 1。

   • cur 表示当前最大得分，可以通过两种方式计算得到：

     1. 当前元素与上一个同奇偶性，则得分为 dp[parity] + nums[i]。

     2. 当前元素与上一个不同奇偶性，则得分为 dp[1 - parity] + nums[i] - x。

   • 更新 dp[parity] 为当前奇偶性情况下的最大得分。

   • 更新 res 为当前最大得分。

4. 返回结果： 返回最终最大得分 res。

代码详解

class Solution {
    public long maxScore(int[] nums, int x) {
        // 初始化
        long res = nums[0];  // 初始化结果为第一个元素的值
        long[] dp = {Integer.MIN_VALUE, Integer.MIN_VALUE}; 
        dp[nums[0] % 2] = nums[0];  // 初始化 dp，依据第一个元素的奇偶性

        for (int i = 1; i < nums.length; i++) {

            // 计算当前元素的奇偶性
            int parity = nums[i] % 2;  

            // 计算当前最大得分
            long cur = Math.max(dp[parity] + nums[i], dp[1 - parity] + nums[i] - x);  

            // 更新 
            res = Math.max(res, cur);  
            dp[parity] = Math.max(dp[parity], cur); 
        }
        return res;
    }
}