前言

在深度学习中，激活函数是神经网络中的一个关键组件，起着引入非线性因素的作用，从而增加神经网络的表达能力和拟合复杂函数的能力。在神经网络中，每个神经元接收来自上一层神经元的输入，并对这些输入进行加权求和，然后将结果输入到激活函数中。激活函数对加权求和的结果进行变换，输出给下一层神经元。通过激活函数，神经网络可以学习和表示数据中的非线性关系，使得其在处理图像、语音、自然语言等复杂任务时表现出色。本文将详细介绍激活函数的定义、作用及其种类，并通过具体例子和代码实现展示每种激活函数的性质和导数。

作用

1. 引入非线性：激活函数引入了非线性因素，使得神经网络可以学习和表示非线性关系。如果没有激活函数，多层神经网络就变成了单一的线性变换，无法拟合复杂的数据分布和模式。

2. 实现分段线性变换：一些激活函数（如ReLU）可以实现分段线性变换，使得神经网络能够学习到不同区间内的不同线性关系，提高了网络的灵活性和表达能力。

3. 去除数据的线性相关性：激活函数可以打破输入数据的线性相关性，使得神经网络可以学习到更复杂的特征和模式，提高了网络的泛化能力。

4. 限制输出范围：某些激活函数（如Sigmoid和Tanh）可以将神经元的输出限制在一个特定的范围内（如0到1或-1到1），有助于控制神经元输出的幅度。

总的来说，激活函数在神经网络中扮演着非常重要的角色，通过引入非线性，增强了网络的表达能力，使得神经网络可以更好地拟合复杂的数据分布和模式。

激活函数种类

目前深度学习中常用的激活函数有以下几种：

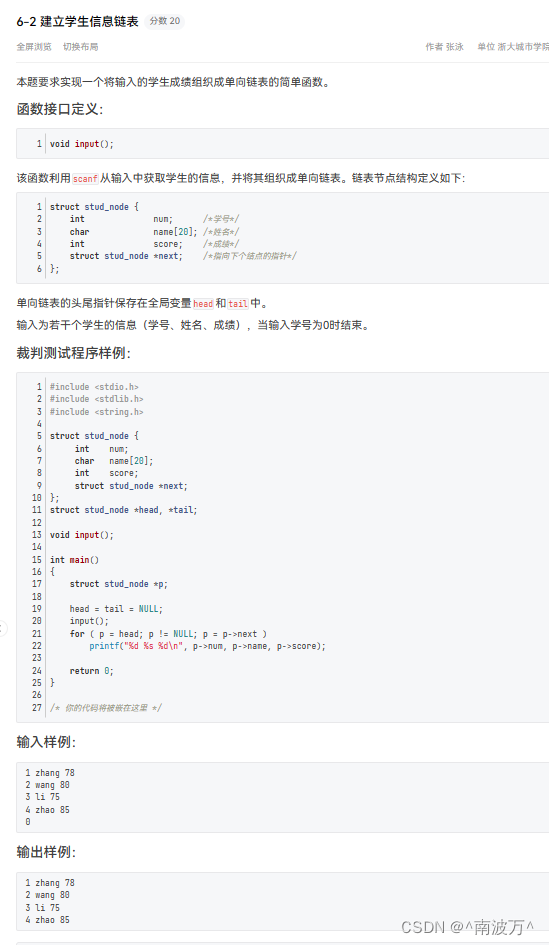
1. ReLU (Rectified Linear Unit)

ReLU函数将所有负值都设为零，保持正值不变。优点是计算简单且有效，但可能导致神经元输出稀疏性，且在负值区域不具备梯度。

• 公式
  $$\text{ReLU}(x)=\max (0,x)$$
• 激活函数图像
  
• 导数公式
  $${\text{ReLU}}^{\prime }(x)=\{\begin{array}{ll}1,& \text{if }x>0\\ 0,& \text{if }x\le 0\end{array}$$ReLU 函数在不同区间上的导数是不一样的。
• 求导后的图像
  
• 特点
  计算简单且有效，但可能导致神经元输出稀疏性，且在负值区域不具备梯度。
• Python 代码实现图像

  import numpy as np
  import matplotlib.pyplot as plt
  
  # 定义输入范围
  x = np.linspace(-10, 10, 400)
  
  # 计算 ReLU 激活函数值
  y = np.maximum(0, x)
  
  # 绘制 ReLU 激活函数图像
  plt.plot(x, y, label="ReLU")
  plt.title("ReLU Activation Function")
  plt.xlabel("x")
  plt.ylabel("ReLU(x)")
  plt.legend()
  plt.grid(True)
  plt.show()
  
  # 计算 ReLU 激活函数的导数值
  y_prime = np.where(x > 0, 1, 0)
  
  # 绘制 ReLU 激活函数导数图像
  plt.plot(x, y_prime, label="ReLU Derivative")
  plt.title("Derivative of ReLU Activation Function")
  plt.xlabel("x")
  plt.ylabel("ReLU'(x)")
  plt.legend()
  plt.grid(True)
  plt.show()
  

2. Leaky ReLU

为了解决ReLU在负值区域没有梯度的问题，Leaky ReLU引入了一个小的斜率（通常很小，如0.01）以保证负值区域也有梯度。

• 公式
  $$f(x)=\{\begin{array}{ll}x,& \text{if }x>0\\ ax,& \text{otherwise}\end{array}$$
  其中 a 是一个小的正数（例如 0.01），用于控制负值区域的斜率。
• 激活函数图像- 求导公式
  $$f^{\prime }(x)=\{\begin{array}{ll}1& \text{if }x\ge 0\\ \alpha & \text{if }x<0\end{array}$$
• 求导后的图像
  
• Python 代码实现图像

  import matplotlib.pyplot as plt
  import numpy as np
  
  def leaky_relu(x, alpha=0.01):
      return np.where(x >= 0, x, alpha * x)
  
  x = np.linspace(-10, 10, 400)
  y = leaky_relu(x)
  
  plt.plot(x, y, label="Leaky ReLU")
  plt.title("Leaky ReLU Activation Function")
  plt.xlabel("x")
  plt.ylabel("f(x)")
  plt.legend()
  plt.grid()
  plt.show()
  
  def leaky_relu_derivative(x, alpha=0.01):
      return np.where(x >= 0, 1, alpha)
  
  dy = leaky_relu_derivative(x)
  
  plt.plot(x, dy, label="Leaky ReLU Derivative")
  plt.title("Leaky ReLU Derivative")
  plt.xlabel("x")
  plt.ylabel("f'(x)")
  plt.legend()
  plt.grid()
  plt.show()
  

3. ELU (Exponential Linear Unit)

ELU在负值区域引入了一个指数增长的梯度，以解决ReLU存在的梯度稀疏性问题。

• 公式
  $$\text{ELU}(x)=\{\begin{array}{ll}x& \text{if }x\ge 0\\ \alpha (e^x-1)& \text{if }x<0\end{array}$$
  其中， $\alpha$ 是一个超参数，通常为正数，控制负半轴的饱和程度。这个激活函数在 $x\ge 0$ 时表现为线性，在 $x<0$ 时表现为指数形式，具有较好的性质，如避免了 ReLU 激活函数在负数区域的“死亡”问题。

• 激活函数图像:
  

• 求导公式
  ELU 激活函数的导数可以分别对 $x\ge 0$ 和 $x<0$ 两个区域求导：$${\text{ELU}}^{\prime }(x)=\{\begin{array}{ll}1& \text{if }x\ge 0\\ \alpha e^x& \text{if }x<0\end{array}$$

• 推导过程

  1. 对于 $x\ge 0$:
     $$\begin{gathered} \text{ELU}(x)=x \\ \frac{d}{dx}\text{ELU}(x)=\frac{d}{dx}x=1 \end{gathered}$$
  2. 对于 $x<0$:
     $$\begin{gathered} \text{ELU}(x)=\alpha (e^x-1) \\ \frac{d}{dx}\text{ELU}(x)=\alpha \frac{d}{dx}(e^x-1)=\alpha e^x \end{gathered}$$

• 求导后的图像:
  

• Python 代码实现图像

  import numpy as np
  import matplotlib.pyplot as plt
  
  def elu(x, alpha=1.0):
      return np.where(x >= 0, x, alpha * (np.exp(x) - 1))
  
  def elu_derivative(x, alpha=1.0):
      return np.where(x >= 0, 1, alpha * np.exp(x))
  
  # 创建输入数据
  x = np.linspace(-3, 3, 400)
  y = elu(x)
  y_prime = elu_derivative(x)
  
  # 创建图像
  plt.figure(figsize=(14, 6))
  
  # ELU函数图像
  plt.subplot(1, 2, 1)
  plt.plot(x, y, label='ELU')
  plt.title('ELU Activation Function')
  plt.xlabel('x')
  plt.ylabel('ELU(x)')
  plt.legend()
  plt.grid()
  
  # ELU导数图像
  plt.subplot(1, 2, 2)
  plt.plot(x, y_prime, label='ELU Derivative', color='red')
  plt.title('ELU Derivative Function')
  plt.xlabel('x')
  plt.ylabel("ELU'(x)")
  plt.legend()
  plt.grid()
  
  # 显示图像
  plt.tight_layout()
  plt.show()
  

4. Sigmoid

Sigmoid函数将输入压缩到0到1之间，在输出值接近饱和时梯度接近于零，容易造成梯度消失问题。

• 公式
  $$\sigma (x)=\frac{1}{1+e^{-x}}$$
• 激活函数图像
  
• 求导公式
  $${\sigma }^{\prime }(x)=\sigma (x)\cdot (1-\sigma (x))$$
  其中 $\sigma (x)$ 是 Sigmoid 函数的值。
• 求导后的图像
  
• Python 代码实现图像

  import numpy as np
  import matplotlib.pyplot as plt
  
  # Sigmoid函数
  def sigmoid(x):
      return 1 / (1 + np.exp(-x))
  
  # Sigmoid函数的导数
  def sigmoid_derivative(x):
      sx = sigmoid(x)
      return sx * (1 - sx)
  
  # 定义输入范围
  x = np.linspace(-10, 10, 400)
  
  # 计算Sigmoid函数值和导数值
  sigmoid_values = sigmoid(x)
  sigmoid_derivative_values = sigmoid_derivative(x)
  
  # 绘制Sigmoid函数图像
  plt.figure(figsize=(12, 6))
  
  plt.subplot(1, 2, 1)
  plt.plot(x, sigmoid_values, label='Sigmoid')
  plt.title('Sigmoid Function')
  plt.xlabel('x')
  plt.ylabel('σ(x)')
  plt.legend()
  
  # 绘制Sigmoid函数导数图像
  plt.subplot(1, 2, 2)
  plt.plot(x, sigmoid_derivative_values, label='Sigmoid Derivative', color='red')
  plt.title('Sigmoid Derivative Function')
  plt.xlabel('x')
  plt.ylabel('σ\'(x)')
  plt.legend()
  
  plt.tight_layout()
  plt.show()
  

5. Tanh

Tanh函数将输入压缩到-1到1之间，Tanh函数与Sigmoid函数类似，但输出均值为0，收敛速度比Sigmoid函数更快。

• 公式
  $$\text{Tanh}(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$
• 激活函数图像
  
• 求导公式
  $${\text{Tanh}}^{\prime }(x)=1-{\text{Tanh}}^2(x)$$
  这是因为：
  $$\frac{d}{dx}\left(\frac{e^x-e^{-x}}{e^x+e^{-x}}\right)=1-{\left(\frac{e^x-e^{-x}}{e^x+e^{-x}}\right)}^2$$
• 求导后的图像
• Python 代码实现图像

  import numpy as np
  import matplotlib.pyplot as plt
  
  # 定义 Tanh 函数
  def tanh(x):
      return np.tanh(x)
  
  # 定义 Tanh 函数的导数
  def tanh_derivative(x):
      return 1 - np.tanh(x)**2
  
  # 定义 x 轴范围
  x = np.linspace(-10, 10, 400)
  
  # 计算 y 轴值
  y = tanh(x)
  y_derivative = tanh_derivative(x)
  
  # 绘制 Tanh 函数
  plt.figure(figsize=(12, 6))
  
  plt.subplot(1, 2, 1)
  plt.plot(x, y, label='Tanh(x)')
  plt.title('Tanh Activation Function')
  plt.xlabel('x')
  plt.ylabel('Tanh(x)')
  plt.legend()
  plt.grid(True)
  
  # 绘制 Tanh 函数的导数
  plt.subplot(1, 2, 2)
  plt.plot(x, y_derivative, label="Tanh'(x)", color='r')
  plt.title('Derivative of Tanh Function')
  plt.xlabel('x')
  plt.ylabel("Tanh'(x)")
  plt.legend()
  plt.grid(True)
  
  plt.tight_layout()
  plt.show()
  

6. Swish

Swish函数是一个新提出的激活函数，在ReLU的基础上引入了一个可学习的参数，通常表现比ReLU更好。

• 公式
  $$\text{Swish}(x)=x\cdot \sigma (x)$$
  其中，$\sigma (x)$ 是 Sigmoid 函数。
• 激活函数图像
• 求导公式
  $$\frac{d}{dx}(\text{Swish}(x))=\text{Swish}(x)+\sigma (x)\cdot (1-\text{Swish}(x))$$
  其中，$\text{Swish}(x)=x\cdot \sigma (x)$，$\sigma (x)$ 是 Sigmoid 函数。
• 激活函数图像
  
• Python 代码实现图像

  import numpy as np
  import matplotlib.pyplot as plt
  
  # 定义 Sigmoid 函数
  def sigmoid(x):
      return 1 / (1 + np.exp(-x))
  
  # 定义 Swish 激活函数
  def swish(x):
      return x * sigmoid(x)
  
  # 定义 Swish 激活函数的导数
  def swish_derivative(x):
      sig = sigmoid(x)
      swish_value = swish(x)
      return swish_value + sig * (1 - swish_value)
  
  # 定义 x 范围
  x = np.linspace(-10, 10, 400)
  
  # 计算 Swish 函数值和导数值
  swish_values = swish(x)
  swish_derivative_values = swish_derivative(x)
  
  # 绘制 Swish 函数图像
  plt.figure(figsize=(12, 6))
  
  plt.subplot(1, 2, 1)
  plt.plot(x, swish_values, label='Swish(x)')
  plt.title('Swish Activation Function')
  plt.xlabel('x')
  plt.ylabel('Swish(x)')
  plt.legend()
  plt.grid(True)
  
  # 绘制 Swish 函数的导数图像
  plt.subplot(1, 2, 2)
  plt.plot(x, swish_derivative_values, label="Swish'(x)", color='r')
  plt.title('Derivative of Swish Activation Function')
  plt.xlabel('x')
  plt.ylabel("Swish'(x)")
  plt.legend()
  plt.grid(True)
  
  plt.tight_layout()
  plt.show()
  

结论

本文详细介绍了几种常用的激活函数，包括ReLU、Leaky ReLU、ELU、Sigmoid、Tanh和Swish。这些激活函数各有优劣，通过引入非线性，提高了神经网络的表达能力，使得其能够拟合复杂的数据分布和模式。理解和选择合适的激活函数对于设计高效的神经网络至关重要。通过具体的公式、导数和Python实现，我们可以更直观地理解每种激活函数的特点及其在不同情况下的表现。未来的研究可以继续探索新的激活函数，进一步提高深度学习模型的性能和效率。