前言：

  今天下午才刚看到oj上发了这次练习，我已经错过了截止时间，刚好不是很想复习六级，就把这次练习补了吧。

正文：

Problem:A 尺取Language：

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
int a[N];
int book[N],book2[N];
int n,cnt=0,ans=0x3f3f3f;
int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		if(book[a[i]]==0){
			book[a[i]]++;
			cnt++;
		}
	}
	//cout<<cnt<<endl;
	int l=0,r=0,cnt2=0;
	while(l<=r&&r<=n){
		//cout<<cnt<<cnt2<<endl;
		if(cnt2<cnt){
			r++;
			if(book2[a[r]]==0){
				cnt2++;
			}
			book2[a[r]]++;
		}
		else{
			ans=min(ans,r-l+1);
			book2[a[l]]--;
			if(book2[a[l]]==0)cnt2--;
			l++;
		}
	}
	cout<<ans<<endl;
	return 0;
}

根据字母出现次数来判断是否包含所有。

Problem:B 尺取-Graveyard Design：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n;
typedef struct stu{
	int t;
	int l;
	int r;
}ans;
ans anss[1000];
int main(){
	cin>>n;
	ll l=1,r=1,cnt=0,tmp=1;
	while(l<=r&&r<=(int)sqrt(n)+2){
		if(tmp<n){
			r++;tmp+=r*r;
		}
		else{
			if(tmp==n){
				anss[++cnt]={r-l+1,l,r};
			}
			tmp-=l*l;
			l++;
		}
		//cout<<l<<" "<<r<<endl;
	}
	cout<<cnt<<endl;
	for(int i=1;i<=cnt;i++){
		cout<<anss[i].t<<" ";
		for(int j=anss[i].l;j<=anss[i].r;j++){
			cout<<j<<" ";
		}
		cout<<endl;
	}
	return 0;
}

数据是小于10^14，记得开long long，然后就是经典的尺取，注意答案先用自定义的结构体存下来，记得输出个数和长短。

Problem:C 尺取-Sum of Consecutive Prime Numbers：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+5;
int prime[N],b[N];
void init(){
	int cnt=0;
	for(int i=2;i<=N;i++){
		if(b[i]==0){
			prime[++cnt]=i;
			for(int j=1;j*i<=N;j++){
				b[j*i]=1;
			}
		}
	}
}
int main(){
	init();
	int x;
	while(cin>>x){
		if(x==0)return 0;
		int l=1,r=1,cnt=2,ans=0;
		while(l<=r&&prime[r]<=x){
			if(cnt<x){
				r++;
				cnt+=prime[r];
			}
			else{
				if(cnt==x)ans++;
				cnt-=prime[l];
				l++;
			}
		}
		cout<<ans<<endl;
	}
	return 0;
}

先算出规定范围内的素数数组，再进行尺取。

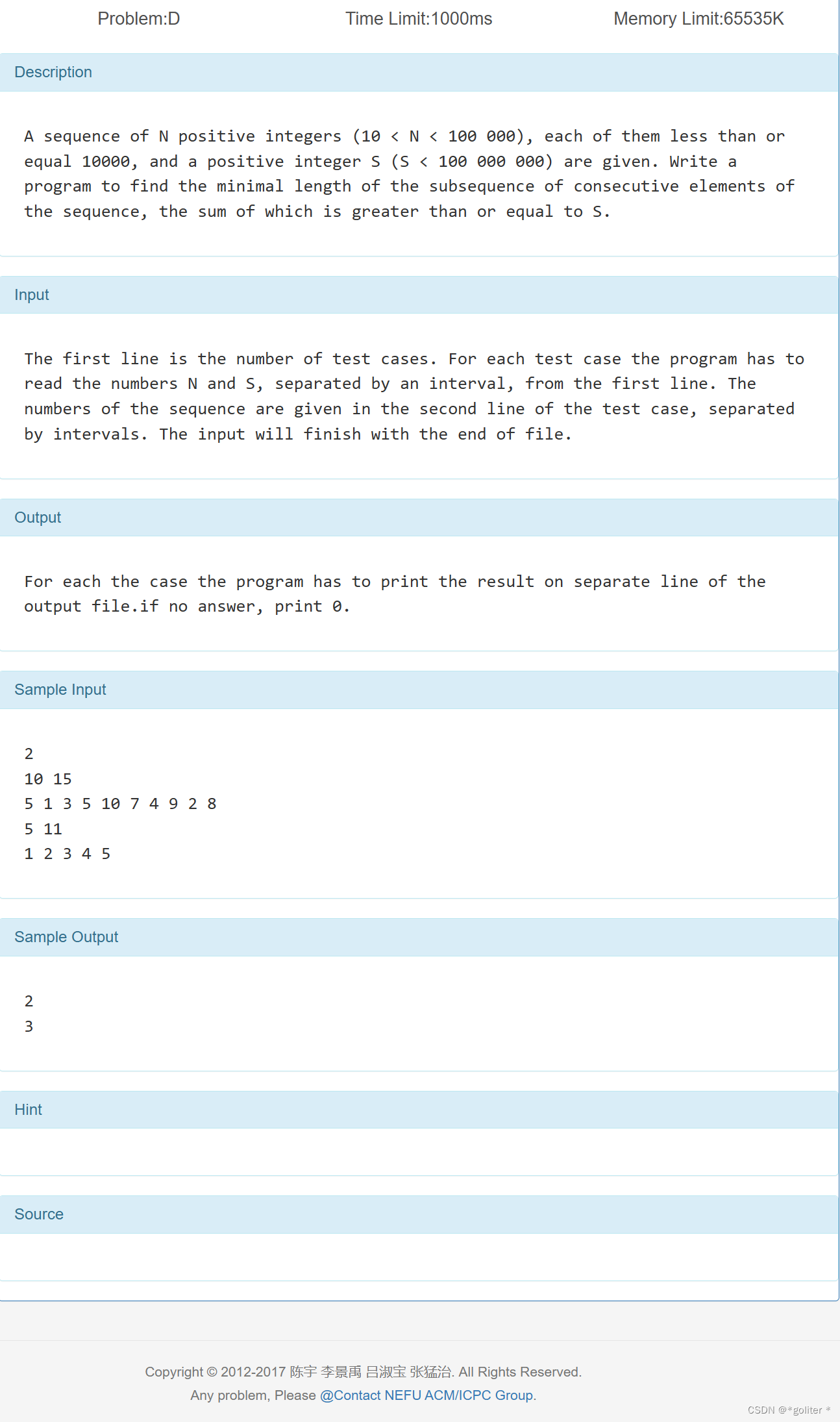
Problem:D 尺取-序列：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+5;
ll a[N];
int main(){
	int t;
	cin>>t;;
	while(t--){
		ll n,s;
		cin>>n>>s;
		for(int i=1;i<=n;i++){
			cin>>a[i];
		}
		ll l=0,r=0;ll cnt=0,ans=0x3f3f3f;
		while(l<=r&&r<=n){
			if(cnt<s){
				r++;
				cnt+=a[r];
			}
			else{
				ans=min(ans,r-l+1);
				cnt-=a[l];
				l++;
			}
		}
		cout<<ans<<endl;
	}
	return 0;
}

这应该是尺取最标准的模板题了，求满足条件的子序列的最小长度。

Problem:E 尺取-字符串：

#include<bits/stdc++.h>
using namespace std;
int book[100000];
int main(){
	string s;
	int cnt2=1,ans=106;
	cin>>s;
	int l=0,r=0;book[s[0]]++;
	while(l<=r&&r<s.size()){
		if(cnt2<26){
			r++;
			if(book[s[r]]==0)cnt2++;
			book[s[r]]++;
		}
		else{
			ans=min(ans,r-l+1);
			book[s[l]]--;
			if(book[s[l]]==0)cnt2--;
			l++;
		}
	}
	cout<<ans<<endl;
	return 0;
}

依旧是通过记录次数来判断条件是否成立和指针移动情况。

Problem:F 林大实验林场--尺取法：

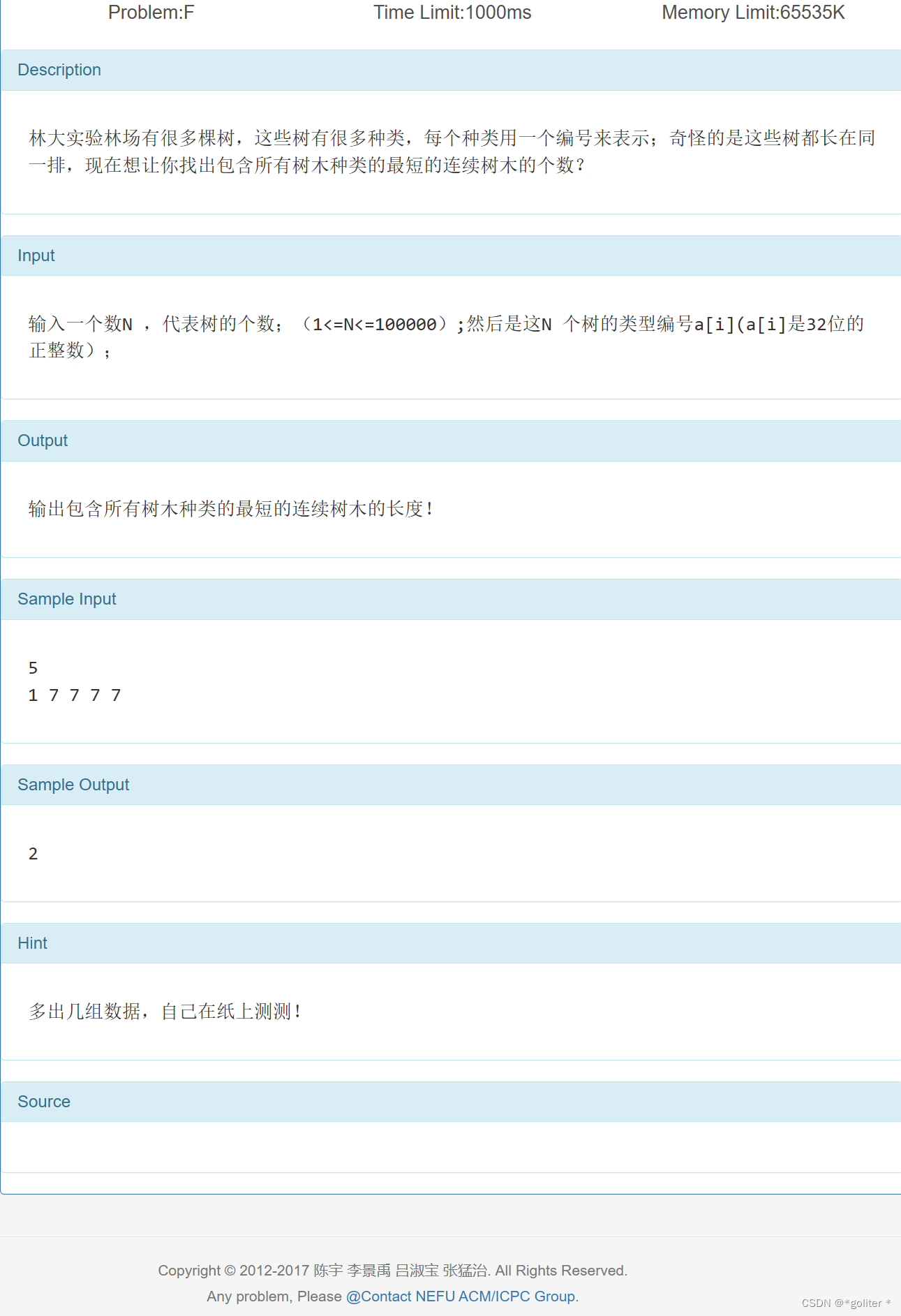
和A题一个代码，没什么好说的。

后记：

  英语六级就要开始了，我连真题都还没刷几道，离考试越近反而学习激情少了许多。最近也开始考虑后面的专业（转，主要是cs,ce或大数据）选择与未来大学学习的规划了，是卷绩点保研（其实自己好像也卷不过）还是根据网上的一些学习路线去面向就业（好像自己也找不到），目前还是很纠结的，感觉不管做哪种选择都有点后悔啊（