题目分析
题目描述的已经十分清楚了,不做过多阐述

算法原理
状态表示
我们假设第i天的最大利润是dp[i]
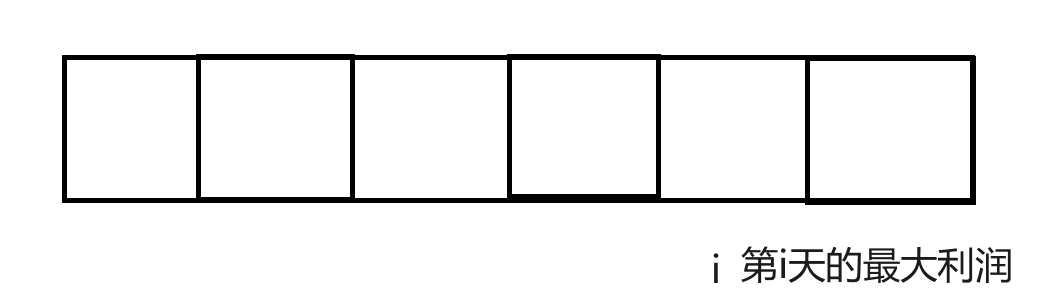
我们来画一下状态机
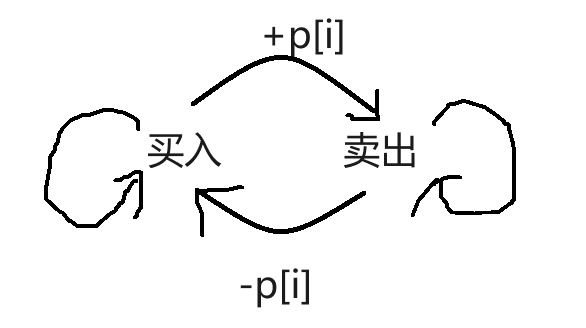
有两个状态,买入后和卖出后,我们就可以使用两个dp表来解决问题
f[i]表示当天买入后的最大利润
g[i]表示当天卖出后的最大利润
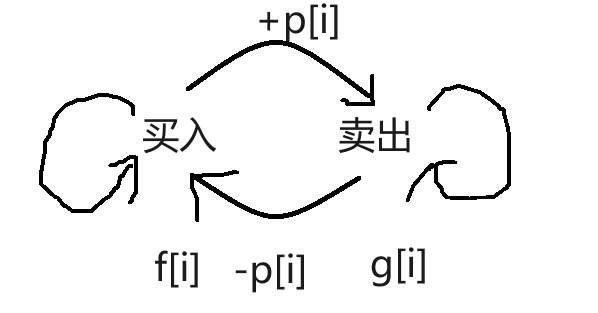
状态转移方程
由状态机可以看出,
买入后,当天如果不卖出,最大利润为前一天买入的最大利润f[i-1],
同理,卖出后,当天如果不买入,最大利润为前一天卖出后的最大利润g[i-1],
如果前一天处于买入状态,当天卖出,最大利润为f[i-1]+p[i],
同理,如果前一天处于卖出状态,当天买入,最大利润为g[i-1]-p[i]
f[i]=max(f[i-1],g[i-1]-prices[i-1]);
g[i]=max(g[i-1],f[i-1]+prices[i-1]);
初始化
f[0]初始化为-p[0],
在第 0 天买入股票,这时候利润是 -prices[0]。
g[0]初始化为0,
在第 0 天不持有股票,这时候利润是 0,因为我们还没有进行任何操作。
填表
必须从左向右填写,需要与当天的股票价格相匹配
确定返回值
结合题目要求+状态要求
本题返回g[n]
解法
class Solution {
public:
int maxProfit(vector<int>& prices) {
//创建dp表
//初始化
//填表
//返回值
int n=prices.size();
vector<int> f(n+1);
auto g=f;
f[0]=-prices[0];
for(int i=1;i<=n;i++)
{
f[i]=max(f[i-1],g[i-1]-prices[i-1]);
g[i]=max(g[i-1],f[i-1]+prices[i-1]);
}
return g[n];
}
};