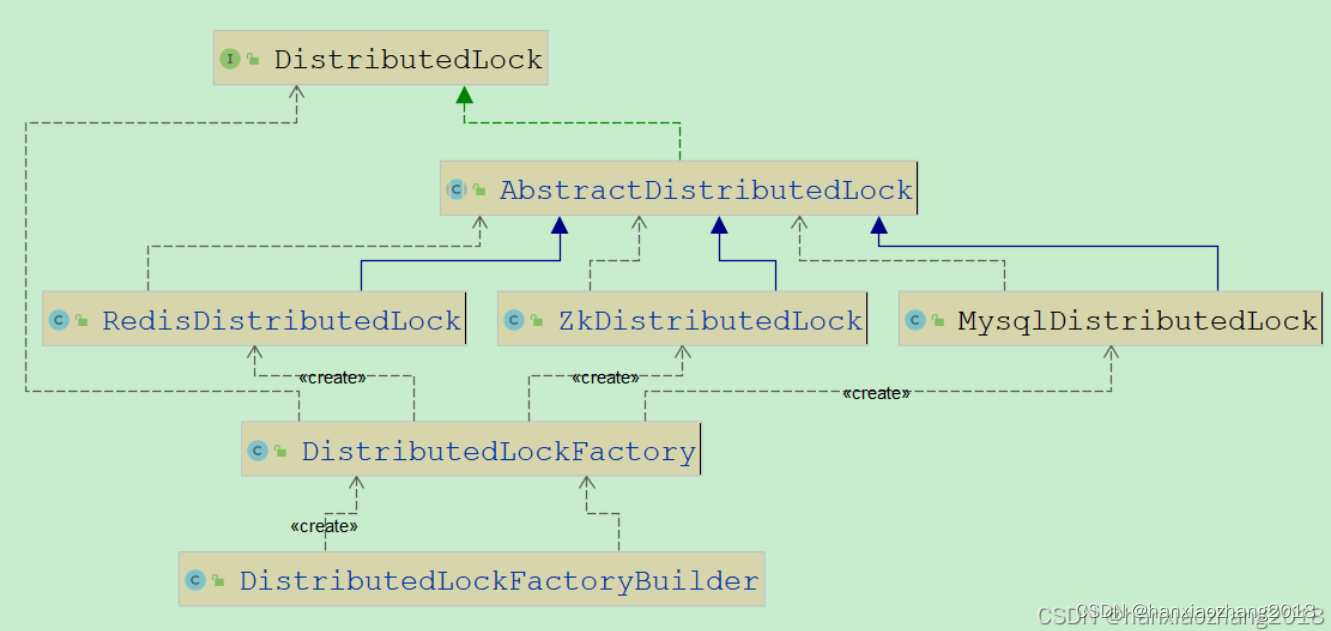
【log4】log4cplus：使用详解（一）

news2025/1/11 14:43:01

1、源码下载

源码下载地址：https://sourceforge.net/projects/log4cplus/files/log4cplus-stable/

最新稳定版本为2.1.1（2023-11-17）
在这里插入图片描述

github中有最新的源码：https://github.com/log4cplus/log4cplus

2、源码编译

1）解压后，进入源码目录中，执行配置命令：

./configure --prefix=/home/laoer/install/log4cplus/2.1.1

2）编译安装

make -j8
make install

</

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1820265.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

智能制造前沿：ARMxy工控机在机器人控制中

智能制造前沿：ARMxy工控机在机器人控制中

机器人控制系统正逐步成为现代制造业的核心引擎。在这个过程中&#xff0c;ARMxy工业计算机以其独特的优势&#xff0c;成为了驱动这一变革的关键力量。本文将以自动化装配线机器人为例&#xff0c;探讨ARMxy如何通过其低功耗、高性能特性&#xff0c;以及高度灵活性的设计&…
阅读更多...
【代码随想录算法训练营第三十五天】 | 1005.K次取反后最大化的数组和 134.加油站 135.分发糖果

【代码随想录算法训练营第三十五天】 | 1005.K次取反后最大化的数组和 134.加油站 135.分发糖果

贪心章节的题目&#xff0c;做不出来看题解的时候&#xff0c;千万别有 “为什么这都没想到” 的感觉&#xff0c;想不出来是正常的&#xff0c;转变心态 “妙啊&#xff0c;又学到了新的思路” &#xff0c;这样能避免消极的心态对做题效率的影响。 134. 加油站 按卡哥的思路…
阅读更多...
【调试笔记-20240613-Linux-在 git 多分支间合并】

【调试笔记-20240613-Linux-在 git 多分支间合并】

调试笔记-系列文章目录 调试笔记-20240613-Linux-在 git 多分支间合并 文章目录 调试笔记-系列文章目录调试笔记-20240613-Linux-在 git 多分支间合并 前言一、调试环境操作系统&#xff1a;Ubuntu 22.04.4 LTS调试环境调试目标 二、调试步骤在远端 git 服务器建立多个分支在本…
阅读更多...
车间降温设备怎么选？有哪些注意事项

车间降温设备怎么选？有哪些注意事项

在选择车间降温设备时&#xff0c;需要考虑多个因素以确保选择的设备能够满足降温需求&#xff0c;同时考虑成本、效率和维护的便捷性。以下是一些关键的注意事项和选择标准&#xff1a; 一、选择标准 厂房大小与结构 厂房的面积、高度和结构将影响空气流通和降温效果。例如&…
阅读更多...
揭秘软件测试秘籍：测试用例设计方法大揭秘

揭秘软件测试秘籍：测试用例设计方法大揭秘

文章目录 引言一、等价类划分1.1 定义1.2 步骤1.3 等价类划分优点和缺点 二、边界值分析法2.1 定义2.2 步骤2.3 边界值分析法的优点和缺点 三、判定表法3.1 定义3.2 步骤3.3 判定表组成不分3.4 判定表的优点和缺点 四、正交实验法4.1 定义4.2 步骤4.3 正交实验法的优点和缺点 五…
阅读更多...
论文研读｜以真实图像为参考依据的AIGC检测

论文研读｜以真实图像为参考依据的AIGC检测

前言&#xff1a;这篇文章介绍几篇AIGC检测的相关工作&#xff0c;其中前几篇文章是以真实图像的特征作为标准进行检测&#xff0c;最后一篇文章就当拓展一下知识边界吧&#xff5e; 目录 Detecting Generated Images by Real Images Only (202311 arXiv)Let Real Images be as…
阅读更多...
WebGL渲染引擎优化方向 -- 内存管理的优化

WebGL渲染引擎优化方向 -- 内存管理的优化

作者&#xff1a;caven chen 对此系列感兴趣还可以看前文&#xff1a; WebGL渲染引擎优化方向 -- 加载性能优化 WebGL渲染引擎优化方向——渲染帧率的优化 前言 WebGL 是一种强大的图形渲染技术&#xff0c;可以在浏览器中快速渲染复杂的 3D 场景。但是&#xff0c;由于 W…
阅读更多...
MySQL与PostgreSQL关键对比三（索引类型）

MySQL与PostgreSQL关键对比三（索引类型）

目录 索引类型 B-tree 索引 Hash 索引 Full-text 索引 GiST 索引 GIN 索引 BRIN 索引 索引创建示例 MySQL PostgreSQL 结论 以下SQL语句的执行如果需要开发工具支持&#xff0c;可以尝试使用SQLynx或Navicat来执行。 MySQL和PostgreSQL在索引方面有许多相似之处&am…
阅读更多...
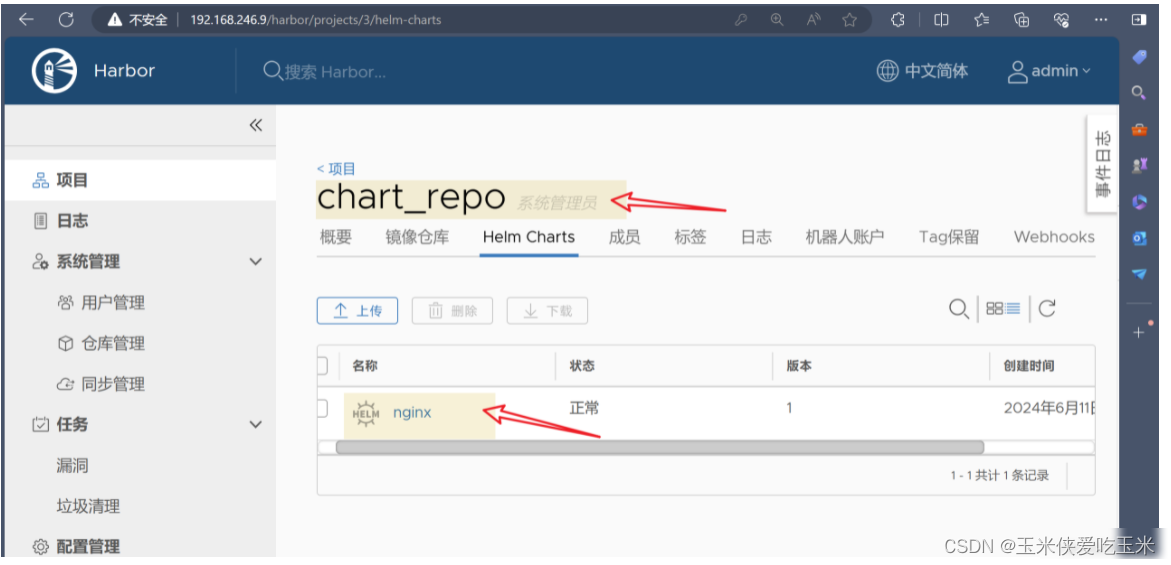
【kubernetes】k8s中包管理工具-----Helm 超详细解读

【kubernetes】k8s中包管理工具-----Helm 超详细解读

目录 一、Helm 1.1什么是 Helm 1.2Helm 有三个重要的概念 1.2.1Chart 1.2.2Repository&#xff08;仓库&#xff09; 1.2.3Release 1.3Helm3 与 Helm2 的区别 二、Helm 部署 2.1安装 helm 2.2命令补全 2.3使用 helm 安装 Chart 2.3.1添加常用的 chart 仓库 2.3.2…
阅读更多...
vue 和 js写屏幕自适应

vue 和 js写屏幕自适应

实现屏幕自适应的方式有很多种&#xff0c;可以通过插件本身提供的方法&#xff0c;可以通过flex布局等&#xff0c;今天我们来写写通过js实现屏幕自适应。 以下是在vue中实现的屏幕自适应 首先在data中定义一下屏幕的默认大小和缩放比例 然后在mounted中获取窗口的内置宽高&a…
阅读更多...
使用 Vue 和 Ant Design 实现抽屉效果的模块折叠功能

使用 Vue 和 Ant Design 实现抽屉效果的模块折叠功能

功能描述&#xff1a; 有两个模块&#xff0c;点击上面模块的收起按钮时&#xff0c;上面的模块可以折叠&#xff0c;下面的模块随之扩展 代码实现&#xff1a; 我们在 Vue 组件中定义两个模块的布局和状态管理&#xff1a; const scrollTableY ref(560); // 表格初始高度…
阅读更多...
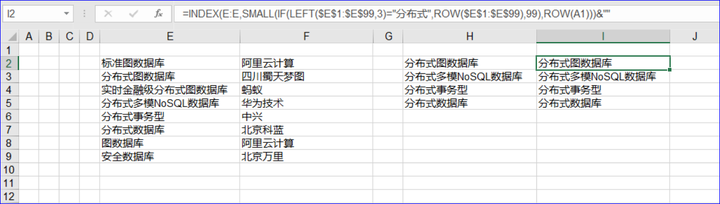
Excel中如何用公式列出包含特定文本的所有单元格？

Excel中如何用公式列出包含特定文本的所有单元格？

如下图&#xff0c;希望用公式得到“以分布式开始”的G列数据。 一、高版本公式 FILTER(E2:E9,LEFT(E2:E9,3)"分布式") 用LEFT函数提取数据的左侧3个字符&#xff0c;是“分布式”的就是以它开始的数据了&#xff0c;用FILTER函数筛选出来即可。 二、低版本公式 如…
阅读更多...
【智能算法应用】基于A星算法求解六边形栅格地图路径规划

【智能算法应用】基于A星算法求解六边形栅格地图路径规划

目录 1.算法原理2.结果展示3.参考文献4.代码获取 1.算法原理 精准导航&#xff1a;用A*算法优化栅格地图的路径规划【附Matlab代码】 六边形栅格地图 分析一下地图&#xff1a; 六边形栅格地图上移动可以看做6领域运动&#xff0c;偶数列与奇数列移动方式有所差异&#xff0…
阅读更多...
【FreeRTOS】内存管理

【FreeRTOS】内存管理

目录 1 为什么要自己实现内存管理2 FreeRTOS的5中内存管理方法2.1 Heap_12.2 Heap_22.3 Heap_32.4 Heap_4 2.5 Heap_53 Heap相关的函数3.1 pvPortMalloc/vPortFree3.2 xPortGetFreeHeapSize 3.3 xPortGetMinimumEverFreeHeapSize3.4 malloc失败的钩子函数 参考《FreeRTOS入门与…
阅读更多...
CleanMyMac是否有必要购买?2024年6.18有什么优惠活动？

CleanMyMac是否有必要购买?2024年6.18有什么优惠活动？

CleanMyMac X是专业的Mac应用卸载,清理优化,软件管理更新工具,兔八哥爱分享获取cleanmymac激活码更安全,让你的Mac电脑焕然一新 CleanMyMacX是一款强大的Mac清理和优化工具&#xff0c;针对系统垃圾、恶意软件和隐私保护提供解决方案。重度用户因其高效性能和全面功能可能需要…
阅读更多...
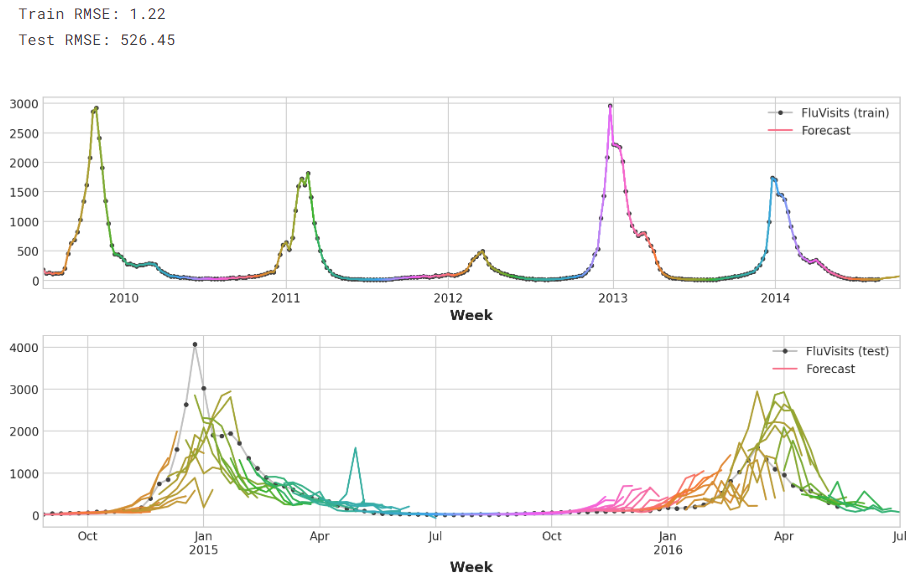
Python学习从0开始——Kaggle时间序列002

Python学习从0开始——Kaggle时间序列002

Python学习从0开始——Kaggle时间序列002 一、作为特征的时间序列1.串行依赖周期 2.滞后序列和滞后图滞后图选择滞后 3.示例 二、混合模型1.介绍2.组件和残差3.残差混合预测4.设计混合模型5.使用 三、使用机器学习进行预测1.定义预测任务2.为预测准备数据3.多步骤预测策略3.1 M…
阅读更多...
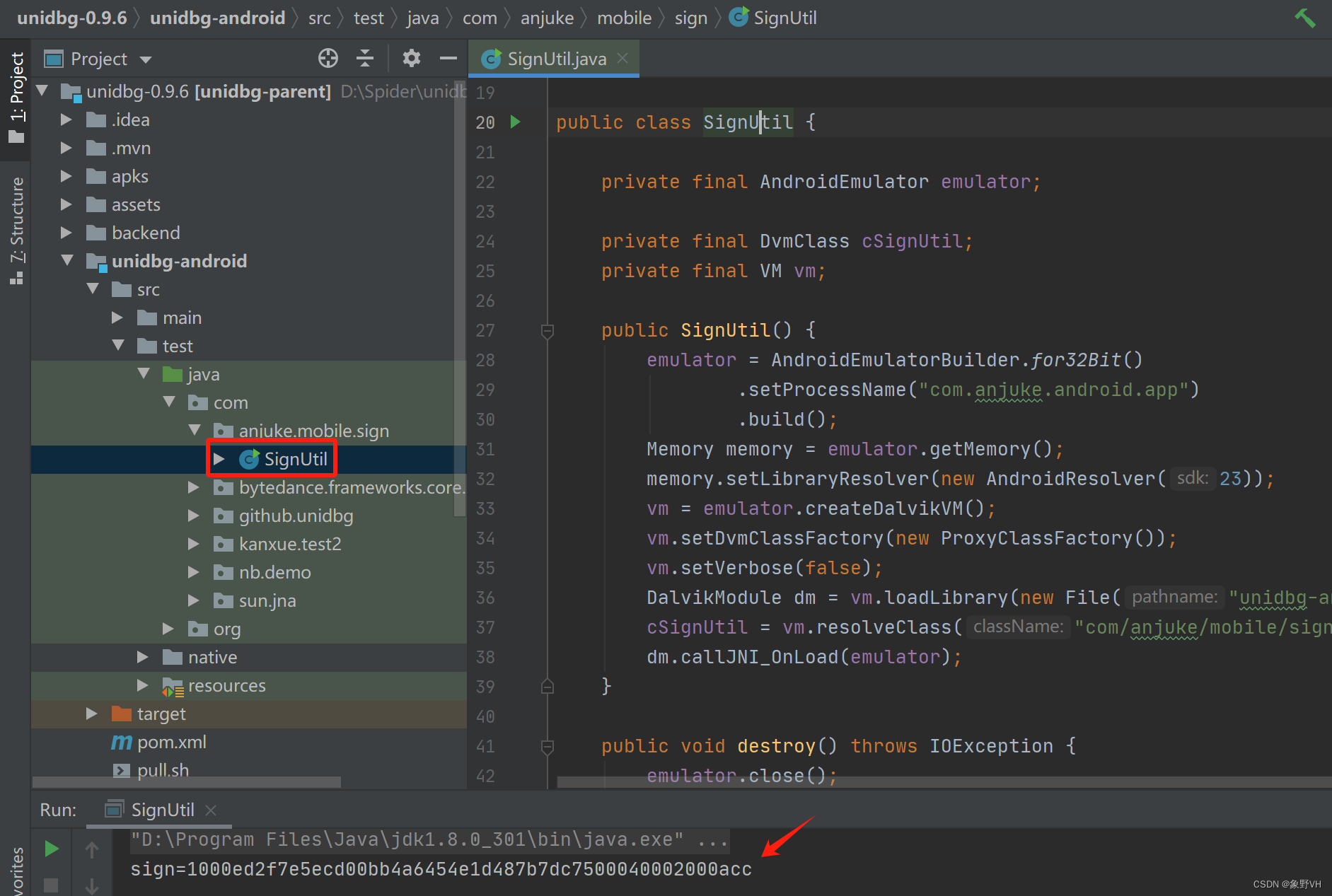
unidbg讲解V1

unidbg讲解V1

前言 unidbg是什么？ unidbg是一个Java项目，可以帮助我们去模拟一个安卓或IOS设备，用于去执行so文件中的算法，从而不需要再去逆向他内部的算法。最终会产出一个jar包，可以被python进行调用。 如何使用unidbg？ 下载github上开源的项目：https://github.com/zhkl0228/un…
阅读更多...
Java基础面试重点-3

Java基础面试重点-3

41. 简述线程生命周期(状态) 其它参考《多线程重点》中的说法。三种阻塞&#xff1a; 等待阻塞&#xff1a; 运行的线程执行o.wait()方法&#xff08;该线程已经持有锁&#xff09;&#xff0c;JVM会把该线程放入等待队列中。同步阻塞&#xff1a; 运行的线程在获取对象的同步…
阅读更多...
Kafka高频面试题整理

Kafka高频面试题整理

文章目录 1、什么是Kafka?2、kafka基本概念3、工作流程4、Kafka的数据模型与消息存储机制1)索引文件2)数据文件 5、ACKS 机制6、生产者重试机制:7、kafka是pull还是push8、kafka高性能高吞吐的原因1&#xff09;磁盘顺序读写&#xff1a;保证了消息的堆积2&#xff09;零拷贝机…
阅读更多...
YOLOv9改进策略 | 损失函数篇 | 利用SlideLoss助力YOLOv9有效涨点（附代码 + 完整修改方式）

YOLOv9改进策略 | 损失函数篇 | 利用SlideLoss助力YOLOv9有效涨点（附代码 + 完整修改方式）

一、本文介绍 本文给大家带来的是分类损失 SlideLoss损失函数&#xff0c;我们之前看那的那些IoU都是边界框回归损失&#xff0c;和本文的修改内容并不冲突&#xff0c;所以大家可以知道损失函数分为两种一种是分类损失另一种是边界框回归损失&#xff0c;上一篇文章里面我们总…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023