合并区间
56. 合并区间 - 力扣(LeetCode)
按照左边界从小到大排序之后,如果 intervals[i][0] <= intervals[i - 1][1] 即intervals[i]的左边界 <= intervals[i - 1]的右边界,则一定有重叠。(本题相邻区间也算重贴,所以是<=)
这么说有点抽象,看图:(注意图中区间都是按照左边界排序之后了)
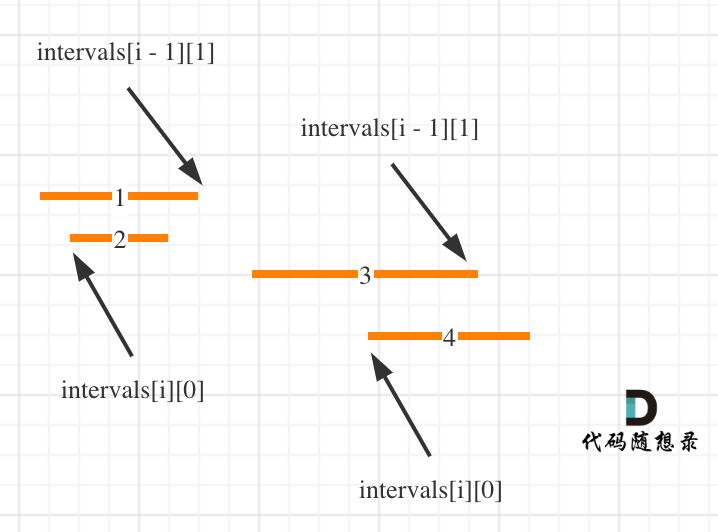
判断左右区间如果没有重叠那么直接加入list否则更新右区间
代码:
public static int[][] merge(int[][] intervals) {
Arrays.sort(intervals, new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return o1[0] - o2[0];
}
});
LinkedList<int[]> res = new LinkedList<>();
int left=intervals[0][0];
int right=intervals[0][1];
for(int i=1;i<intervals.length;i++){
if(intervals[i][0]<=right){
right=Math.max(right,intervals[i][1]);
}else{
res.add(new int[]{left,right});
left=intervals[i][0];
right=intervals[i][1];
}
}
res.add(new int[]{left,right});
return res.toArray(new int[res.size()][]);
}
单调递增的数字
738. 单调递增的数字 - 力扣(LeetCode)
例如:98,一旦出现strNum[i - 1] > strNum[i]的情况(非单调递增),首先想让strNum[i - 1]--,然后strNum[i]给为9,这样这个整数就是89,即小于98的最大的单调递增整数。
此时是从前向后遍历还是从后向前遍历呢?
从前向后遍历的话,遇到strNum[i - 1] > strNum[i]的情况,让strNum[i - 1]减一,但此时如果strNum[i - 1]减一了,可能又小于strNum[i - 2]。
这么说有点抽象,举个例子,数字:332,从前向后遍历的话,那么就把变成了329,此时2又小于了第一位的3了,真正的结果应该是299。
那么从后向前遍历,就可以重复利用上次比较得出的结果了,从后向前遍历332的数值变化为:332 -> 329 -> 299
代码:
class Solution {
public int monotoneIncreasingDigits(int N) {
String[] strings = (N + "").split("");
int start = strings.length;
for (int i = strings.length - 1; i > 0; i--) {
if (Integer.parseInt(strings[i]) < Integer.parseInt(strings[i - 1])) {
strings[i - 1] = (Integer.parseInt(strings[i - 1]) - 1) + "";
start = i;
}
}
for (int i = start; i < strings.length; i++) {
strings[i] = "9";
}
return Integer.parseInt(String.join("",strings));
}
}