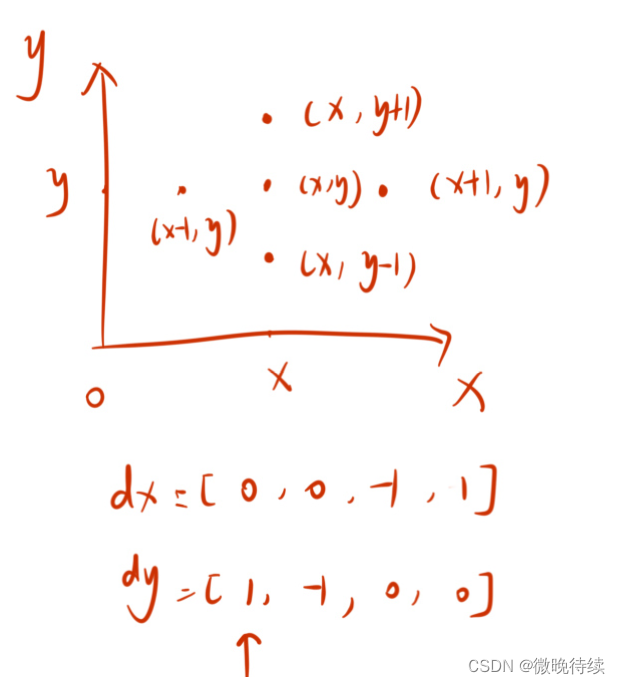第一题
295. 数据流的中位数
本题我们是求解给定数组的中位数。且由于需要随时给数组添加元素,所以我们要求解该动态数组的中位数,所以本题最关键的就是维护数组在添加元素之后保持有序的排序,这样就能很快的求解中位数;
解法:我们使用大小堆来维护数据流的中位数
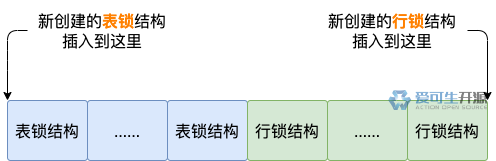
如上图所示,我们将当前数组从中间分为两部分,左边部分的数据放入到大根堆,右边数据放入到小根堆,且两个堆的数据长度只有两种情况,要么两的个堆里面数据相同,要么左堆的长度比右堆的长度多一;
接下来就是分类讨论添加数据的详细情况:
步骤一:
定义大根堆的堆顶元素为x,里面元素的个数为m;小根堆堆顶的元素为y,里面元素的个数为n;
步骤二:
当m等于n时:
添加元素nums小于等于x或者当前两个堆都为空时,nums元素直接进入到左边大根堆;添加元素nums大于x时,nums元素首先进入到右边小根堆,然后将右边小根堆的堆顶元素放入到左边大根堆中;
步骤三:
当m等于n+1时:
添加元素nums大于x时,nums元素直接进入到右边小根堆;
添加元素nums小于等于x时,nums元素首先进入到左边大根堆,然后将左边大根堆的堆顶元素放入到右边小根堆中;
步骤四:
根据情况求取该数组的中位数;
综上所述,代码如下:
class MedianFinder { PriorityQueue<Integer> left; PriorityQueue<Integer> right; public MedianFinder() { left = new PriorityQueue<Integer>((a,b) -> b - a); right = new PriorityQueue<Integer>((a,b) -> a - b); } public void addNum(int num) { if(left.size() == right.size()){ if(left.isEmpty() || num <= left.peek()){ left.offer(num); }else{ right.offer(num); left.offer(right.poll()); } }else{ if(num <= left.peek()){ left.offer(num); right.offer(left.poll()); }else{ right.offer(num); } } } public double findMedian() { if(left.size() == right.size()) return (left.peek() +right.peek())/2.0; else return left.peek(); } } /** * Your MedianFinder object will be instantiated and called as such: * MedianFinder obj = new MedianFinder(); * obj.addNum(num); * double param_2 = obj.findMedian(); */
第二题
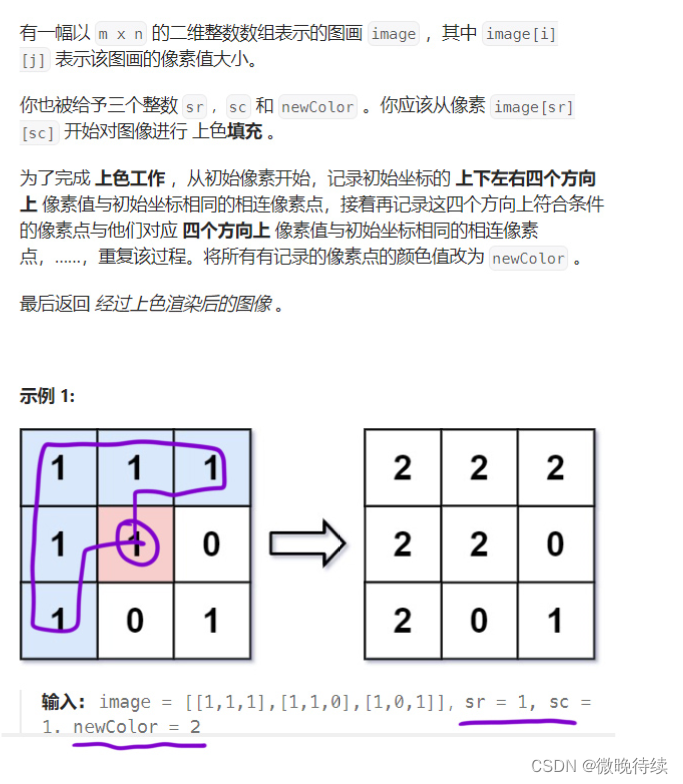
733. 图像渲染
解法:bfs层序遍历
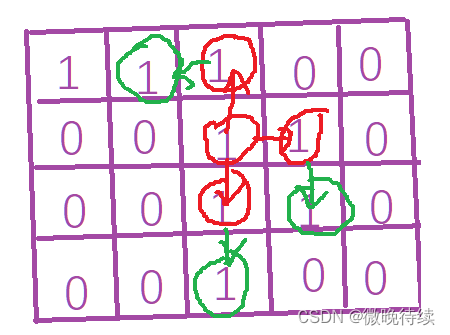
层序遍历如下所示:
假设当前的当前位置如下所示:
第二部就是找到其相邻的:
第三部就是找到第二部中相邻的:
依次类推;
本题的解题步骤如下:
综上所述,代码如下:
步骤一:
创建一个队列,将当前的元素放入到队列里面,并将元素改变颜色;
步骤二:
将队列中的元素先拿出来一个,分析出该元素的坐标,采用象限数组的方式来遍历该元素的上下左右四个位置的元素;
即如下所示:
如果该被遍历到的元素满足条件就将该元素放入到队列中,并将该元素按要求变色;
步骤三:就这样一一拿出队列中的元素,一直重复,直到队列为空为止;
class Solution { //象限坐标数组 int[] dx = {0,0,1,-1}; int[] dy = {1,-1,0,0}; public int[][] floodFill(int[][] image, int sr, int sc, int color) { int prev = image[sr][sc];//统计刚开始的颜色 if(prev == color) return image;//处理边界情况 Queue<int[]> q = new LinkedList<>(); q.add(new int[]{sr,sc}); int m = image.length,n = image[0].length; while(!q.isEmpty()){ int[] t = q.poll(); int a = t[0],b=t[1];//取出收个点的x,y周坐标 //该坐标的上下左右四个点,用向量数组坐标的方法来展示 image[a][b] = color; for(int i = 0;i<4;i++){ int x = a + dx[i],y = b + dy[i]; if(x >= 0 && x <m && y >= 0 && y < n && image[x][y] == prev){ q.add(new int[]{x,y}); } } } return image; } }
第三题
200. 岛屿数量
示例一:
示例二:
解法:本题采用bfs层序遍历的方法,同时采用象限数组小技巧;
本题重新定义一个长度宽度与原题相似的布尔数组vis,每当遍历到一个元素且满足该题意要求是,将vis数组里面相对应位置的元素定义为true,这样在遍历的时候防治该元素被二次遍历;
总体的解题思路如上题故事,代码如下所示:
class Solution { //象限坐标数组 int[] dx = {0,0,1,-1}; int[] dy = {1,-1,0,0}; boolean[][] vis = new boolean[301][301]; int m,n; public int numIslands(char[][] grid) { m = grid.length; n = grid[0].length; int ret = 0; for(int i = 0;i < m ;i++){ for(int j = 0;j < n ;j++){ if(grid[i][j] == '1' && !vis[i][j]){ ret++; bfs(grid,i,j); } } } return ret; } public void bfs(char[][] grid,int i,int j){ Queue<int[]> q = new LinkedList<>(); q.add(new int[]{i,j}); vis[i][j] = true; while(!q.isEmpty()){ int[] t = q.poll(); int a = t[0],b = t[1]; for(int s = 0;s < 4;s++){ int x = a +dx[s],y = b + dy[s]; if(x >= 0 && x <m && y >= 0 && y < n && grid[x][y] == '1' && !vis[x][y]){ q.add(new int[]{x,y}); vis[x][y] = true; } } } } }
ps:本次的内容就到这里了,如果对你有所帮助的话就请一一键三连哦!!!