5.冒泡+选择+插入+希尔

news2024/11/17 10:06:26

一、排序算法

排序基础
1.排序算法的稳定性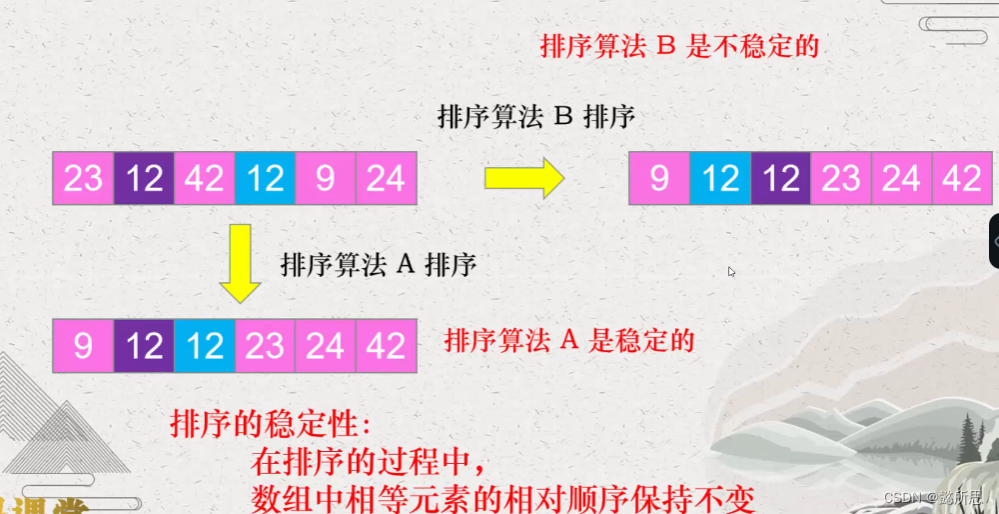在这里插入图片描述
2.何为原地排序算法
在这里插入图片描述

1.冒泡排序

在这里插入图片描述
从下面第一个元素开始往上冒泡，一轮冒泡下来，最大的元素就去了最上面了
在这里插入图片描述
步骤：无序数组
在这里插入图片描述
每次冒泡都可以将最大的元素放到最右边去
第一轮比较了5次：
在这里插入图片描述
第二轮比较了4次：
在这里插入图片描述
第三轮比较了3次：
在这里插入图片描述
。。。
第四轮比较了2次
。。。
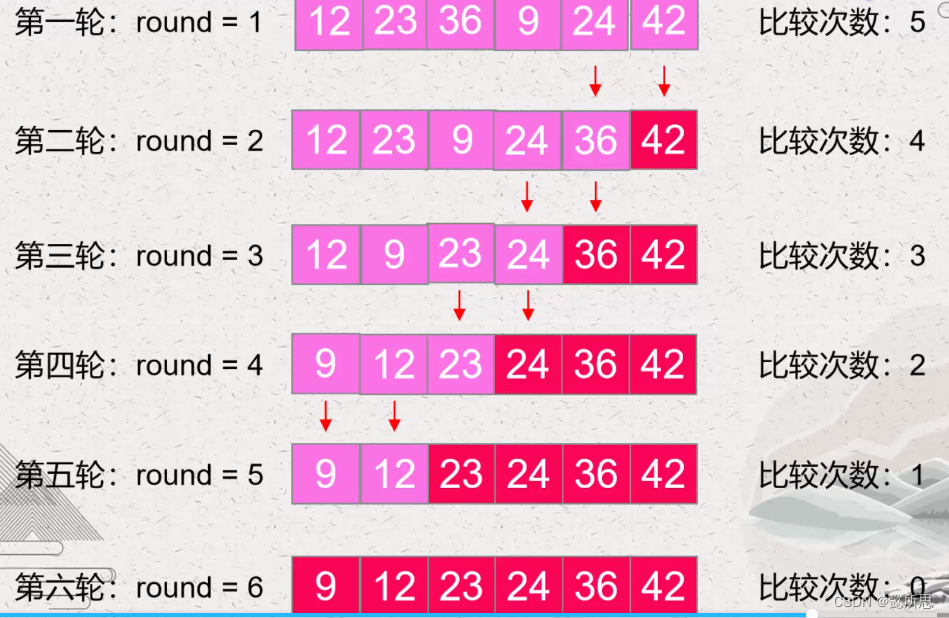
在这里插入图片描述
有6个元素比较了6次，第一次比较了5次，第二次4次。。。
code：
两次遍历，第一次控制冒泡的轮数，第二次控制每次比较次数

public class BubbleSorter {
    public void sort(int[] data){
        if(data == null || data.length <=1) return;
        for (int round = 1; round <= data.length; round++) { //控制冒泡的轮数
            int compareTimes = data.length - round;
            for (int i = 0; i < compareTimes; i++) {   //控制每轮比较次数
                if(data[i]>data[i+1]){
                    int tmp = data[i];
                    data[i] = data[i+1];
                    data[i+1] = tmp;
                }
            }
        }
    }

    public static void main(String[] args) {
        int[] data = new int[]{12,23,36,9,24,42};
        new BubbleSorter().sort(data);
        System.out.println(Arrays.toString(data));
    }
}

特点

  • 时间复杂度分析：
    时间复杂度：O(n²)
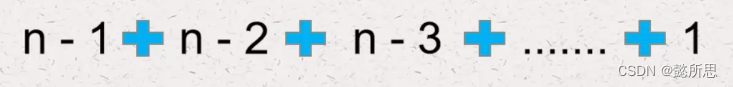
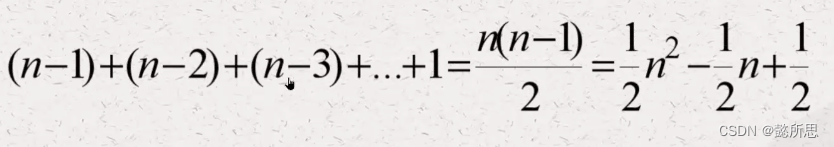
    在这里插入图片描述
    在这里插入图片描述
  • 空间复杂度为O(1)，原地排序算法
  • 冒泡排序是稳定的排序算法
    在这里插入图片描述
    只有大于才进行交换，两个36的位置不会改变
    优化：减少元素交换次数
    在这里插入图片描述
    在这里插入图片描述
    在第二轮中已经是有序的了，就不需要再进行第三轮、第四轮交换了

代码实现

public class BubbleSorter {
    public void sort(int[] data){
        if(data == null || data.length <=1) return;
        
        for (int round = 1; round <= data.length; round++) { //控制冒泡的轮数
            boolean hasSwap = false;
            int compareTimes = data.length - round;
            for (int i = 0; i < compareTimes; i++) {   //控制每轮比较次数
                if(data[i]>data[i+1]){
                    int tmp = data[i];
                    data[i] = data[i+1];
                    data[i+1] = tmp;
                    hasSwap = true;
                }
            }
            //如果没有发生交换就可以退出了
            if(!hasSwap){
                break;
            }
        }
    }

    public static void main(String[] args) {
        int[] data = new int[]{12,23,36,9,24,42};
        new BubbleSorter().sort(data);
        System.out.println(Arrays.toString(data));
    }
}

2. 选择排序

重在选择，每次选择出来一个最小的元素和前面的元素进行交换
选择排序的步骤：
1.找到数组中最小的数组元素
2.将这个最小的数组元素和数组第一个元素进行交换
3.在剩下元素中找到最小的数组元素和数组第二个元素进行交换
。。。
假设第一个元素是最小值，在剩下元素里面找最小值，还需要一个指针 j 来遍历数组找最小值，和 i 进行比较
在这里插入图片描述
遍历到12的时候，12比第一个元素值小，可能是最小值，将其索引放到minNumIndex中
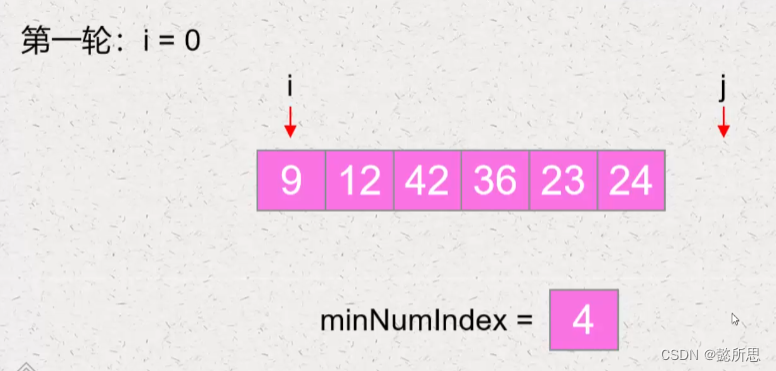
在这里插入图片描述
第一轮遍历完成后就可以找到数组中最小的元素值的索引，存放在minNumIndex中，将这个索引指向的元素和指针i 指向的元素进行交换
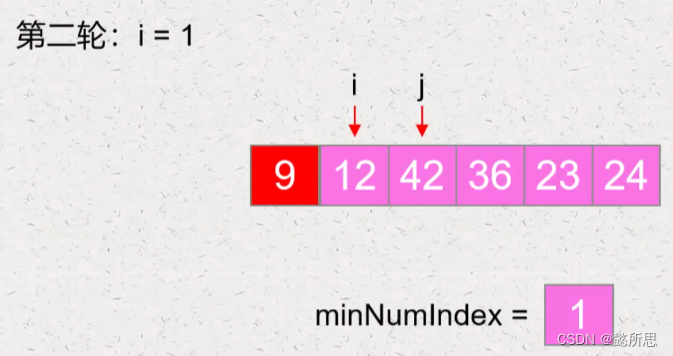
第二轮：
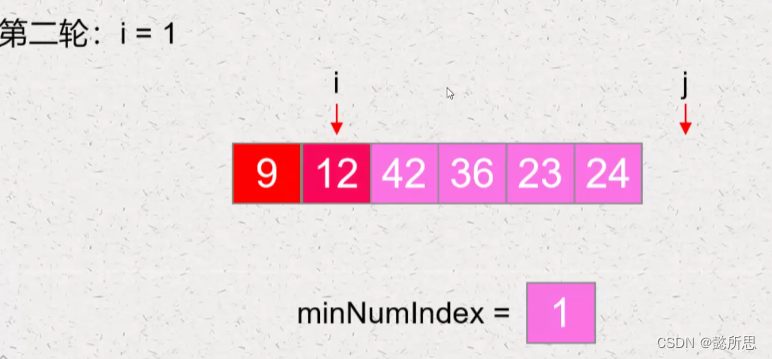
在这里插入图片描述
在这里插入图片描述
第三轮：
在这里插入图片描述
在这里插入图片描述
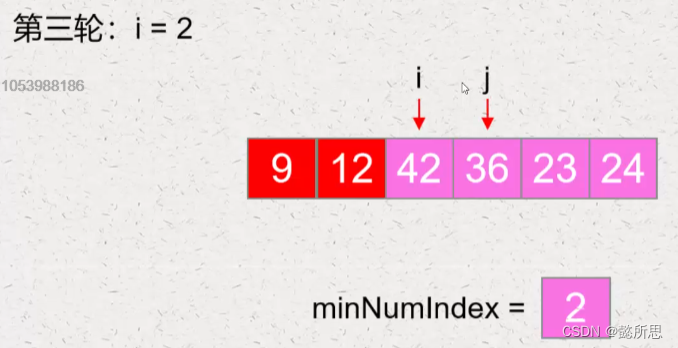
第三轮，找到最小元素值的索引为4，将其和 i 指针指向元素进行交换
。。。
在这里插入图片描述
数组有多少个元素就需要进行多少轮的排序
时间复杂度：O(n²)
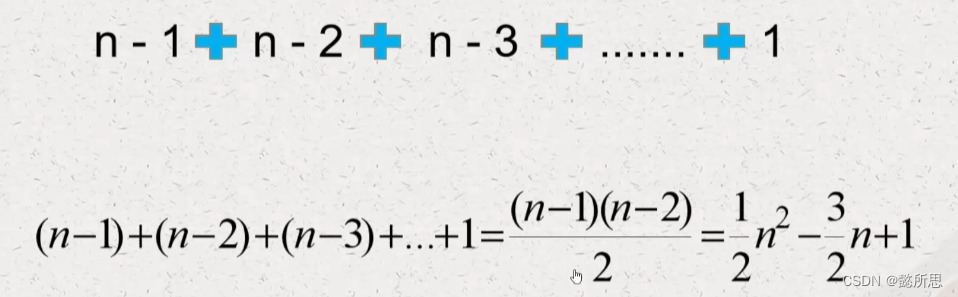
在这里插入图片描述
code:
将交换元素的方法抽取为父类

public class Sorter {
    public void swap(int[] nums,int i,int j){
        int tmp = nums[i];
        nums[i] = nums[j];
        nums[j] = tmp;
    }
}

代码实现

public class SelectionSort extends Sorter{
    public void sort(int[] data){
        if(data == null || data.length<=1) return;

        for (int i = 0; i < data.length; i++) { //控制选择排序的轮数
            //找到[i,n)中的最小元素所在的索引  minNumIndex用来存放最小值的索引
            int minNumIndex = i;
            //j从i+1开始遍历数组，找到最小元素值
            for (int j = i+1; j < data.length; j++) {
                if(data[j]<data[minNumIndex]){
                    minNumIndex = j;
                }
            }
            //将data[i]和最小元素进行交换
            swap(data,i,minNumIndex);
        }
    }

    public static void main(String[] args) {
        int[] data = new int[]{12,23,36,9,24,42};
        new SelectionSort().sort(data);
        System.out.println(Arrays.toString(data));
    }
}

特点

  • 空间复杂度：O(1)，原地排序算法 时间复杂度：O(n²)
  • 选择排序是不稳定的排序算法
    在这里插入图片描述

3. 插入排序

将每一个元素插入到已经有序的数组的位置
在这里插入图片描述
核心思想：取未排序区间的元素在已排序区间中找到合适的插入位置将其插入，并保证已排序区间的数据一直有序，重复这个过程直到未排序区间没有元素为止
一般是假设第一个元素为已排序元素
在这里插入图片描述
插入排序的步骤：有n个元素就进行n轮
第一轮：取第一个元素34，这个元素已经有序
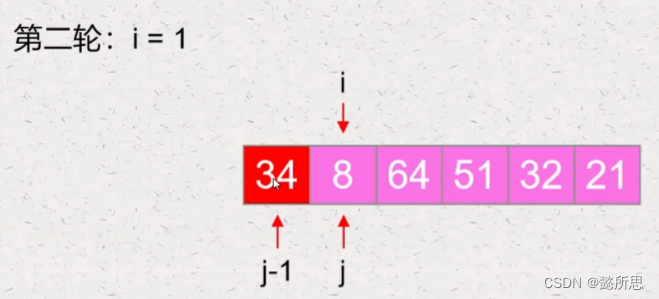
在这里插入图片描述
第二轮：
在这里插入图片描述
从第二个元素开始，对比 j 指向元素和 j-1 元素，如果比 j-1 元素值要小，则进行交换
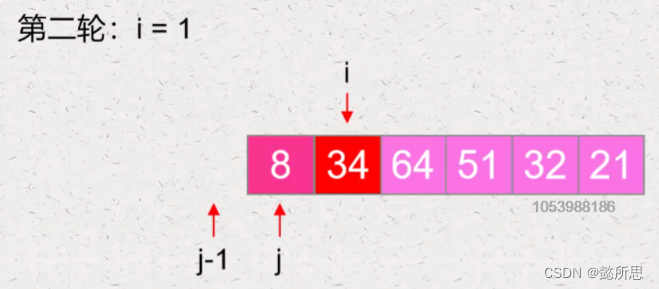
在这里插入图片描述
在这里插入图片描述
第三轮：从第三个元素开始，比前一个元素，位置正确不用动
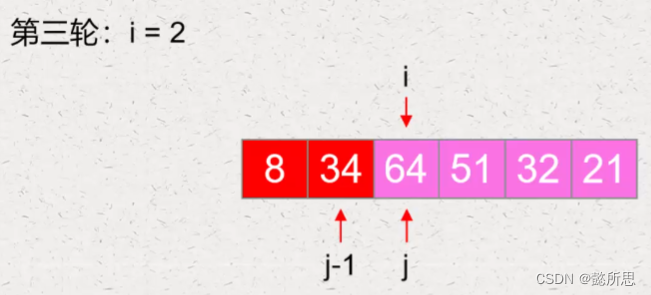
在这里插入图片描述
第四轮：从第四个元素开始，比前一个元素小，要向前移动
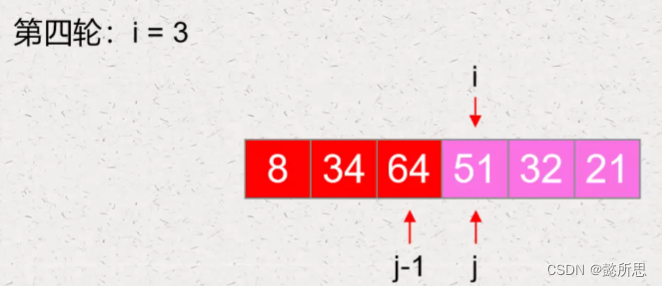
在这里插入图片描述
在这里插入图片描述
进行交换，注意此时，j-1 和 j 需要继续向前移动
第五轮：
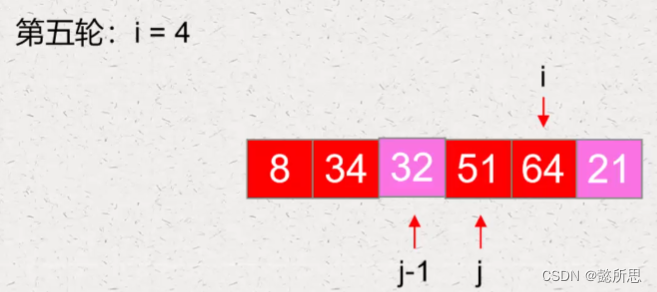
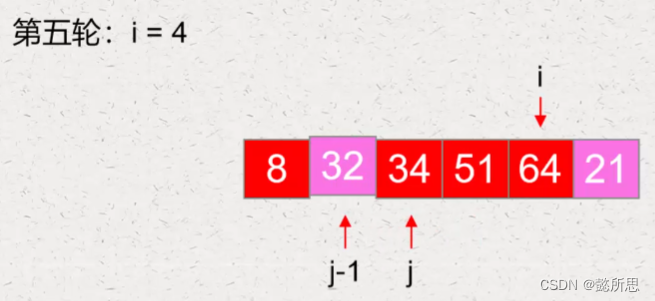
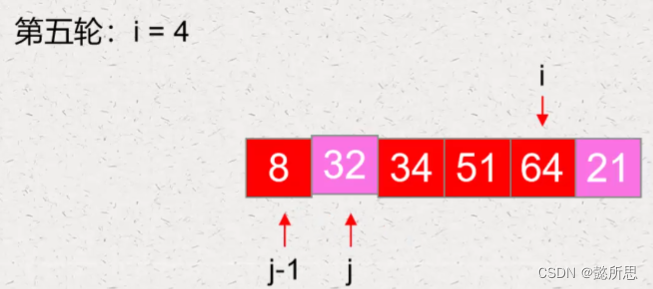
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
第六轮：
在这里插入图片描述

拿到未排序区间的元素，一直往前找，找到合适的位置将这个元素插入进去，一直到未排序区间为空，就表示这个数组排序完成了
时间复杂度：
遍历一遍数组，时间复杂度为O(n)
每轮遍历需要将一个元素插入到有序数组的正确位置这个插入过程的最坏时间复杂度为O(n)
根据乘法法则：O(n²)
code：

代码实现（优化前）

public class InsertionSorter extends Sorter{
    public void sort(int[] data){
        if(data==null||data.length<=1)return;

        for (int i = 1; i < data.length; i++) { //控制插入排序的轮数，第一个元素已经默认有序，可以存第二个开始
            for (int j = i; j > 0 ; j--) {  //j从i开始向前移动，和j-1进行判断，j-1不能小于0，j-1也不能等于0，不然就变成data[-1]了
                if(data[j] < data[j-1]){
                    swap(data,j,j-1);
                }else{
                    break;
                }
            }
        }
    }

    public static void main(String[] args) {
        int[] data = new int[]{12,23,36,9,24,42};
        new InsertionSorter().sort(data);
        System.out.println(Arrays.toString(data));
    }
}

特点

  • 空间复杂度是O(1)，时间复杂度为O(n²)，原地排序算法
  • 插入排序是稳定的排序算法，可以选择不去进行交换，只有小于的时候才去交换
    在这里插入图片描述

代码实现（优化后）

插入排序的优化：
不使用元素交换，使用赋值代替元素交换，减少元素访问次数
可以将有序数组中较大的元素总是向右移动，然后将元素插入到正确的位置

//优化
public void sort1(int[] data){
    if(data==null||data.length<=1)return;

    for (int i = 1; i < data.length; i++) { //控制插入排序的轮数，第一个元素已经默认有序，可以存第二个开始
        int tmp = data[i];
        int j;
        for (j = i; j > 0 ; j--) {  //j从i开始向前移动，和j-1进行判断，j-1不能小于0，j-1也不能等于0，不然就变成data[-1]了
            if(tmp < data[j-1]){
                //将较大的元素向后移动
                data[j] = data[j-1];
            }else{
                break;
            }
        }
        //找到i 对应的元素需要插入的位置
        data[j] = tmp;
    }
}

冒泡、选择、插入排序性能对比

时间复杂度都是O(n²)
通过比较交换次数来比较性能

package com.douma.line.algo.sort;

import java.util.Random;

/**
 * 对比冒泡、选择、插入排序性能
 */
public class SortCompare {
    private static Random random = new Random();

    private static int[] getData(int n){
        int[] data = new int[n];
        for (int i = 0; i < n; i++) {
            data[i] = random.nextInt();
        }
        return data;
    }

    private static long time(String sortType,int[] data){
        long start = System.currentTimeMillis();

        if(sortType.equals("bubble"))new BubbleSorter().sort(data);
        else if(sortType.equals("selection"))new SelectionSort().sort(data);
        else if(sortType.equals("insertion"))new InsertionSorter().sort(data);

        return System.currentTimeMillis() - start;
    }

    private static long manyTimeSort(String sortType,int n,int k){
        long totalTime = 0;
        for (int i = 0; i < k; i++) {
            totalTime += time(sortType,getData(n));
        }
        return totalTime;
    }

    public static void main(String[] args) {
        double t1 = manyTimeSort("bubble",1000,100);
        double t2 = manyTimeSort("selection",1000,100);
        double t3 = manyTimeSort("insertion",1000,100);
        System.out.println(t1 / t2);    //t1 > t2
        System.out.println(t2 / t3);    //t2 > t3

        //结论：插入排序性能最好(稳定)，其次是选择排序(不稳定)，最后是冒泡排序(稳定)
    }
}

推荐使用插入排序，性能最好，是稳定的
插入排序有两种实现方式，一种是基于交换实现的；另一种是基于赋值实现的；赋值的效率要比交换效率要高

4. 希尔排序

什么是希尔排序？
是对插入排序的优化
如果有一个大规模乱序数组插入排序很慢，因为它只会交换相邻的两个元素
在这里插入图片描述
这个大规模数组在进行若干次插入排序后，前面已经有序了，最后一个是最小的元素，这个时候需要将最小元素一步步的向前比较移动，
在这里插入图片描述
这个过程会非常慢
希尔排序就可以解决大规模数组插入排序慢的问题

希尔排序的思想：
先使数组中任间隔为h(4)的元素有序，然后对全局(也就是h=1)进行排序
希尔排序递增序列计算公式
间隔h的取值逻辑
在这里插入图片描述
在这里插入图片描述
最常用的是：
在这里插入图片描述
递增序列的取值：
在这里插入图片描述
使用公式计算得出h取值，k取1,2,3,4,5带入公式计算出h取值，h应该小于N/3

public class ShellSorter {
    public void sort(int[] data){
        if(data == null || data.length <=1)return;

        //1.计算递增序列
        int n = data.length;
        ArrayList<Integer> list = new ArrayList<>();
        int k = 1;
        int h;
        do{
            h = (int)(Math.pow(3,k)-1)/2;
            if(h > n/3)break;
            list.add(h);    // 1,4,13,40,121....
            k++;
        }while (h <= n/3);
    }
}

倒序遍历递增序列

//2.希尔排序
for (k = list.size()-1; k >=0 ; k--) {  //倒序遍历递增序列
    h = list.get(k);
    // 将数组变为 h 有序

}

希尔排序详细步骤
希尔排序过程 h = 4，经过此次排序，间隔为4的元素就局部有序了
全局排序 h =1

代码实现

public class ShellSorter extends Sorter{
    public void sort(int[] data){
        if(data == null || data.length <=1)return;

        //1.计算递增序列
        int n = data.length;
        ArrayList<Integer> list = new ArrayList<>();
        int k = 1;
        int h;
        do{
            h = (int)(Math.pow(3,k)-1)/2;
            if(h > n/3)break;
            list.add(h);    // 1,4,13,40,121....
            k++;
        }while (h <= n/3);

        //2.希尔排序
        for (k = list.size()-1; k >=0 ; k--) {  //倒序遍历递增序列
            h = list.get(k);
            // 将数组变为 h 有序
            for (int i = h; i < n; i++) { //倒序遍历
                for (int j = i; j >= h ; j=j-h) {  
                    if(data[j] < data[j-h]){
                        swap(data,j,j-h);
                    }else{
                        break;
                    }
                }
            }
        }
    }

    public static void main(String[] args) {
        int[] data = new int[]{12,23,36,9,24,42};
        new ShellSorter().sort(data);
        System.out.println(Arrays.toString(data));
    }
}

希尔排序对比插入排序性能
性能要比插入排序好，具体要看递增序列h的取值，根据公式获取

特点

希尔排序的特点

  • 空间复杂度：O(1)，原地排序算法
  • 希尔排序是不稳定的排序算法
    在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1818002.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

3D数字化营销——电商行业提升转化率，降低退货率的杀手锏！

3D数字化营销——电商行业提升转化率，降低退货率的杀手锏！

随着3D、AR等前沿技术的蓬勃发展&#xff0c;电商行业正迎来一场3D数字化营销的革命。这种创新的营销方式不仅极大地丰富了商品的展现形式&#xff0c;还成功弥补了传统电商在临场感和体验感方面的不足&#xff0c;从而显著提升了消费者的购物体验。 51建模网为电商行业提供3D…
阅读更多...
C++:十大排序

C++:十大排序

目录 时间复杂度分析 选择排序 引言 算法思想 动图展示 代码实现 (升序) 优化 代码实现 分析 冒泡排序 引言 算法思想 动图展示 代码实现 插入排序 引言 算法思想 动图展示 代码实现 计数排序 引言 算法思想 动图展示 代码实现 桶排序 引言 算法思…
阅读更多...
python学习—合并多个Excel工作簿表格文件

python学习—合并多个Excel工作簿表格文件

系列文章目录 python学习—合并TXT文本文件 python学习—统计嵌套文件夹内的文件数量并建立索引表格 python学习—查找指定目录下的指定类型文件 python学习—年会不能停&#xff0c;游戏抽签抽奖 python学习—循环语句-控制流 文章目录 系列文章目录功能说明1 准备工作&#…
阅读更多...
Python内存管理与垃圾回收机制

Python内存管理与垃圾回收机制

目录 一、引言 二、Python内存管理概述 三、引用计数机制 四、垃圾回收机制 标记-清除&#xff08;Mark-and-Sweep&#xff09; 分代收集&#xff08;Generational Collection&#xff09; 五、内存泄漏与优化 六、总结 一、引言 Python作为一门高级编程语言&#xff…
阅读更多...
基于Java技术的ERP管理系统：企业资源规划的先进解决方案

基于Java技术的ERP管理系统：企业资源规划的先进解决方案

在当前数字化转型的趋势下&#xff0c;企业对于高效、稳定且具备扩展性的管理系统的需求日益增加。为了满足这一需求&#xff0c;我们开发了一款基于Java技术的鸿鹄ERP&#xff08;企业资源规划&#xff09;管理系统。该系统采用了Spring Cloud Alibaba、Spring Boot、MybatisP…
阅读更多...
ArrayList浅析

ArrayList浅析

目录 一、ArrayList源码1.1 迭代器1.1.1 Itr源码浅析1.1.2 ListItr源码浅析 1.2 常用方法1.3 System.arraycopy1.4 ArrayList 的创建方式 二、引申问题2.1 ArrayList的大小是如何增加的&#xff1f;2.2 什么情况下你会使用ArrayList2.3 在索引中ArrayList的增加或者删除某个对象…
阅读更多...
JVM 一些常见问题QA

JVM 一些常见问题QA

GC Roots 虚拟机栈中引用的对象&#xff1b; 本地方法栈中JNI引用的对象&#xff1b; 方法区中类静态变量引用的对象&#xff1b; 方法区中常量引用的对象&#xff1b; Full GC是Minor GCMajor GC吗&#xff1f; Minor GC&#xff1a;回收年轻代&#xff1b; Major GC&…
阅读更多...
比特币私钥公钥地址生成

比特币私钥公钥地址生成

比特币私钥公钥地址生成算法 原理 实现 #!coding:utf8#author:yqq #date:2019/3/4 0004 14:35 #description: 比特币地址生成算法import hashlib import ecdsa import os#2019-05-15 添加私钥限制范围 g_b58 123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz#g…
阅读更多...
写个代码扫描插件，再也不怕 log4j 等问题

写个代码扫描插件，再也不怕 log4j 等问题

引言 关于静态代码扫描&#xff0c;大家想必都非常熟悉了&#xff0c;比如 lint、detekt 等&#xff0c;这些也都是常用的扫描工具。但随着隐私合规在国内越来越趋于常态&#xff0c;我们经常需要考虑某些危险api的调用排查等等&#xff0c;此时上述的工具往往不容易实现现有的…
阅读更多...
PHP开发的爱情盲盒交友系统网站源码

PHP开发的爱情盲盒交友系统网站源码

源码介绍 PHP开发的爱情盲盒交友系统网站源码 独立后台 源码截图 源码下载 PHP开发的爱情盲盒交友系统网站源码
阅读更多...
TCPListen客户端和TCPListen服务器

TCPListen客户端和TCPListen服务器

创建项目 TCPListen服务器 public Form1() {InitializeComponent();//TcpListener 搭建tcp服务器的类&#xff0c;基于socket套接字通信的//1创建服务器对象TcpListener server new TcpListener(IPAddress.Parse("192.168.107.83"), 3000);//2 开启服务器 设置最大…
阅读更多...
Kali Linux 2022.2 发布，包含 10 个新工具和WSL 改进

Kali Linux 2022.2 发布，包含 10 个新工具和WSL 改进

Offensive Security发布了Kali Linux 2022.2&#xff0c;这是2022年的第二个版本&#xff0c;具有桌面增强功能&#xff0c;有趣的愚人节屏幕保护程序&#xff0c;WSL GUI改进&#xff0c;终端调整&#xff0c;最重要的是&#xff0c;新的工具&#xff01; Kali Linux是一个Li…
阅读更多...
Python | Leetcode Python题解之第148题排序链表

Python | Leetcode Python题解之第148题排序链表

题目&#xff1a; 题解&#xff1a; class Solution:def sortList(self, head: ListNode) -> ListNode:def merge(head1: ListNode, head2: ListNode) -> ListNode:dummyHead ListNode(0)temp, temp1, temp2 dummyHead, head1, head2while temp1 and temp2:if temp1.v…
阅读更多...
Django中使用下拉列表过滤HTML表格数据

Django中使用下拉列表过滤HTML表格数据

在Django中&#xff0c;你可以使用下拉列表&#xff08;即选择框&#xff09;来过滤HTML表格中的数据。这通常涉及两个主要步骤&#xff1a;创建过滤表单和处理过滤逻辑。 创建过滤表单 首先&#xff0c;你需要创建一个表单&#xff0c;用于接收用户选择的过滤条件。这个表单可…
阅读更多...
集合java

集合java

1.集合 ArrayList 集合和数组的优势对比&#xff1a; 长度可变 添加数据的时候不需要考虑索引&#xff0c;默认将数据添加到末尾 package com.itheima;import java.util.ArrayList;/*public boolean add(要添加的元素) | 将指定的元素追加到此集合的末尾 | | p…
阅读更多...
E-R数据模型是什么？

E-R数据模型是什么？

概念模型是从现实世界到计算机世界转换的一个中间层次，在数据库设计的过程中它是比较关键的一步。因此，概念模型必须能够真实地反映现实世界中被管理事物的特征及其复杂的联系，即应该具有丰富的语义表达能力和直接模拟现实世界的能力，且具有直观、自然、语义丰富、易于用户…
阅读更多...
「51媒体」媒体邀约-全国邀请媒体现场报道宣传

「51媒体」媒体邀约-全国邀请媒体现场报道宣传

传媒如春雨&#xff0c;润物细无声&#xff0c;大家好&#xff0c;我是51媒体网胡老师。 「51媒体」媒体邀约是一家专注于提供媒体传播方案和执行的服务公司&#xff0c;旨在通过一站式服务帮助企业或个人进行有效的媒体邀约和活动宣传。 「51媒体」提供的不仅仅是简单的媒体邀…
阅读更多...
U盘文件删除如何恢复？4个实用技巧（含图文）

U盘文件删除如何恢复？4个实用技巧（含图文）

“我的u盘里保存了很多重要的文件&#xff0c;但是不知道为什么部分文件丢失&#xff0c;有什么方法可以帮我快速恢复u盘文件的吗&#xff1f;希望大家帮帮我&#xff01;” U盘作为我们日常存储和传输数据的重要工具&#xff0c;其数据的安全性和可恢复性尤为重要。当U盘中的文…
阅读更多...
Vue22-v-model收集表单数据

Vue22-v-model收集表单数据

一、效果图 二、代码 2-1、HTML代码 2-2、vue代码 1、v-model单选框的收集信息 v-model&#xff1a;默认收集的就是元素中的value值。 单选框添加默认值&#xff1a; 2、v-model多选框的收集信息 ①、多个选择的多选 注意&#xff1a; 此处的hobby要是数组&#xff01;&…
阅读更多...
白酒：茅台镇白酒的品鉴会与文化交流活动

白酒：茅台镇白酒的品鉴会与文化交流活动

茅台镇&#xff0c;这个位于中国贵州省的小镇&#xff0c;因其与众不同的自然环境和杰出的酿酒工艺而成为世界著名的白酒产区。云仓酒庄豪迈白酒作为茅台镇的品牌&#xff0c;积极参与各种品鉴会和文化交流活动&#xff0c;向世界展示了中国白酒的魅力和文化底蕴。 近年来&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023