数据结构——02-算数表达式-栈-实验题目分享

news2024/11/28 2:52:46

一、实验题目

算数表达式计算：

设计算法根据用户输入的合法表达式计算结果并显示出来

表达式中的符号为+、-、*、/、（、）

表达式中数字为整数

二、实验环境

Windows 11

Visual Studio Code

（总体代码在最后）

三、实验过程

思路分析：

需要实现一个算法来解析和计算包含加法(+)、减法(-)、乘法(*)、除法(/)以及括号(( ))的合法整数表达式：

根据学过的树的知识，这个表达式可以有三种表达方式： ​ 前缀、中缀、后缀

前缀：将表达式变为前缀后，从右往左，每次从操作数栈取一个数，再取一个操作符，再取一个操作数，进行运算。

后缀：将表达式变为后缀后，从左往右，每次从操作数栈取一个数，再取一个操作符，再取一个操作数，进行运算。

中缀：虽然表达式写出来很适合人类观看，但是对计算机实现来说比较困难，每当遇见一个算术运算符就要看操作符栈是不是空的，如果是空的就直接放进去，如果不是空的就要比较优先级，如果优先级大就进去，如果小就要取出两个数字进行运算再放进去

举个例子：

img

img

img

img

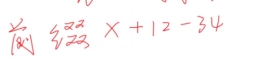
1. 创建两个栈：一个用于存储操作数（数字），另一个用于存储操作符（+、-、*、/）；

2. 从左到右扫描表达式：

如果遇到操作数，将其压入操作数栈。

如果遇到操作符：

        如果操作符栈为空，或者栈顶是左括号，直接将操作符压入操作符栈。

        如果当前操作符的优先级高于操作符栈栈顶的操作符，将当前操作符压入操作符栈。

        否则，从操作数栈中弹出一个操作数和操作符栈的栈顶操作符，执行相应的运算，并将结果压回操作数栈。然后将当前操作符压入操作符栈。

如果遇到左括号，将其压入操作符栈。

        如果遇到右括号，从操作数栈中弹出一个操作数和操作符栈中的操作符，执行运算，并将结果压回操作数栈。重复此过程直到遇到左括号，然后从操作符栈中弹出左括号。

3. 表达式扫描完毕后，如果操作符栈中仍有操作符，重复第二步的过程，直到操作符栈为空。

4. 最后，操作数栈中应该只剩下一个元素，即表达式的结果。

代码：

img

计算函数 (Calculate)：这个函数负责执行基本的算术运算。它从数字栈中弹出两个数字，根据传入的运算符执行相应的运算，并将结果压入数字栈。

img

完整代码请见附件

测试结果：

img

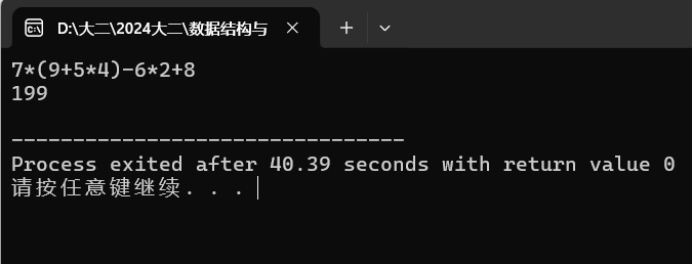
四、结果分析

img

使用这两个结构体来实现数字栈和字符栈

img

压栈

img

主函数 (main)：这是程序的入口点。它首先读取一个表达式，然后初始化数字栈和字符栈。接着，它遍历表达式中的每个字符，如果是数字，则将其转换为浮点数并入栈；如果是运算符，则根据运算符的优先级和栈内的运算符进行比较，然后决定是入栈还是执行计算。最后，当表达式中的所有字符都被处理完毕后，执行剩余的运算符，并将最终结果打印出来。

img

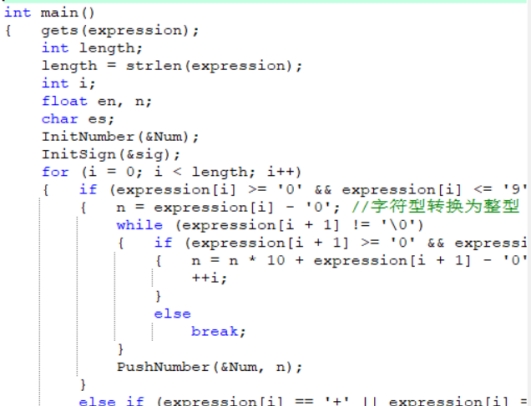
总体代码结构：

1. 输入处理：

  1. 从用户那里获取输入的表达式，并将其转换为字符数组或字符串。

  2. 编写一个函数来检查表达式的合法性，包括括号匹配和操作符的正确使用。

2. 表达式解析：

  1. 实现上述两个栈的逻辑。

  2. 编写一个循环来逐个字符处理表达式。

3. 计算结果：

  1. 根据两个栈的内容执行计算。

  2. 在遇到操作符时，从栈中弹出相应的操作数，执行运算，并压入结果。

4. 输出结果：

  1. 一旦表达式的所有部分都被处理完毕，操作数栈顶的元素就是最终结果。

  2. 显示结果给用户。

五、实验心得

在本次实验中，通过编写和测试一个简单的表达式求值器程序，加深对栈这一数据结构的理解，同时熟悉基本的算术运算和运算符优先级处理，我更加深入地理解了栈的工作原理以及如何利用栈来解决实际问题。

我将具体完成阶段分为三个：设计阶段：首先设计了两个栈结构，一个用于存储操作数（数字），另一个用于存储操作符（字符）。确定了每个栈的基本操作，包括初始化、入栈、出栈和获取栈顶元素。 编码阶段：接着，根据设计实现了主函数和栈操作函数。主函数负责读取表达式并逐个字符进行解析，根据运算符优先级和结合性规则，执行相应的入栈和计算操作。 测试阶段：在完成编码后，我进行了多轮测试，包括简单表达式的计算和错误输入的处理。

程序能够正确处理基本的算术表达式，并返回预期的结果。

学习总结：学习了栈的基本操作和在程序中的应用。 理解了运算符优先级和结合性的概念。 加强了对C语言中字符串处理和字符操作的理解。 意识到了代码测试的重要性，以及如何通过测试来发现并解决问题。

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <malloc.h>
#include <math.h>
#define maximum 100000

typedef struct//数字栈
{	float data[maximum];
	int top;
} number;

typedef struct//字符栈
{	char data[maximum];
	int top;
} sign;

void InitNumber(number *stack);//初始化数字栈
void GetTopNumber(number stack, float *e);//获取栈顶元素
void PushNumber(number *stack, float e);//进栈
void PopNumber(number *stack, float *e);//出栈

void InitSign(sign *stack);
void GetTopSign(sign stack, char *e);
void PushSign(sign *stack, char e);
void PopSign(sign *stack, char *e);

void Calculate(number *stack, char e);

number Num;
sign sig;
char expression[maximum];

int main()
{	gets(expression);
	int length;
	length = strlen(expression);
	int i;
	float en, n;
	char es;
	InitNumber(&Num);
	InitSign(&sig);
	for (i = 0; i < length; i++)
	{	if (expression[i] >= '0' && expression[i] <= '9')
		{	n = expression[i] - '0'; //字符型转换为整型
			while (expression[i + 1] != '\0')
			{	if (expression[i + 1] >= '0' && expression[i + 1] <= '9')
				{	n = n * 10 + expression[i + 1] - '0';
					++i;
				}
				else
					break;
			}
			PushNumber(&Num, n);
		}
		else if (expression[i] == '+' || expression[i] == '-' || expression[i] == '*' || expression[i] == '/'
		         || expression[i] == '^' || expression[i] == '(' || expression[i] == ')')
		{	switch (expression[i])
			{	case '+':
					if (sig.data[sig.top - 1] != '+' && sig.data[sig.top - 1] != '-' && sig.data[sig.top - 1] != '*'
					        && sig.data[sig.top - 1] != '/' && sig.data[sig.top - 1] != '^')
						//与栈顶元素的优先级相比较， 高于时入栈，此处判断是否入栈。
						PushSign(&sig, '+');
					else
					{	while (sig.top > 0 && sig.data[sig.top - 1] != '(') //如果栈不为空切不为左括号，则出栈
						{	PopSign(&sig, &es);
							Calculate(&Num, es);
						}
						PushSign(&sig, '+');
					}
					break;
				case '-':
					if (sig.data[sig.top - 1] != '+' && sig.data[sig.top - 1] != '-' && sig.data[sig.top - 1] != '*'
					        && sig.data[sig.top - 1] != '/' && sig.data[sig.top - 1] != '^')
						PushSign(&sig, '-');
					else
					{	while (sig.top > 0 && sig.data[sig.top - 1] != '(')
						{	PopSign(&sig, &es);
							Calculate(&Num, es);
						}
						PushSign(&sig, '-');
					}
					break;
				case '*':
					if (sig.data[sig.top - 1] != '*' && sig.data[sig.top - 1] != '/' && sig.data[sig.top - 1] != '^')
						PushSign(&sig, '*');
					else
					{	while (sig.top > 0 && sig.data[sig.top - 1] != '(')
						{	PopSign(&sig, &es);
							Calculate(&Num, es);
						}
						PushSign(&sig, '*');
					}
					break;
				case '/':
					if (sig.data[sig.top - 1] != '*' && sig.data[sig.top - 1] != '/' && sig.data[sig.top - 1] != '^')
						PushSign(&sig, '/');
					else
					{	while (sig.top > 0 && sig.data[sig.top - 1] != '(')
						{	PopSign(&sig, &es);
							Calculate(&Num, es);
						}
						PushSign(&sig, '/');
					}
					break;
				case '^':
					if (sig.data[sig.top - 1] != '^')
						PushSign(&sig, '^');
					else
					{	while (sig.top > 0 && sig.data[sig.top - 1] != '(')
						{	PopSign(&sig, &es);
							Calculate(&Num, es);
						}
						PushSign(&sig, '^');
					}
				case '(':
					PushSign(&sig, '(');
					break;
				case ')':
					while (sig.data[sig.top - 1] != '(')
					{	PopSign(&sig, &es);
						Calculate(&Num, es);
					}
					PopSign(&sig, &es);
			}
		}
	}
	while (sig.top > 0)
	{	PopSign(&sig, &es);
		Calculate(&Num, es);
	}
	GetTopNumber(Num, &en);
	printf("%.0f\n", en);
	return 0;
}

void InitNumber(number *stack)
{	stack->top = 0;
}

void GetTopNumber(number stack, float *e)
{	if (stack.top == 0)
		return;
	else *e = stack.data[stack.top - 1];
}

void PushNumber(number *stack, float e)
{	if (stack->top >= maximum)
		return;
	else
		stack->data[stack->top++] = e;
}

void PopNumber(number *stack, float *e)
{	if (stack->top == 0)
		return;
	else *e = stack->data[--stack->top];
}

void InitSign(sign *stack)
{	stack->top = 0;
}

void GetTopSign(sign stack, char *e)
{	if (stack.top == 0)
		return;
	else *e = stack.data[stack.top - 1];
}

void PushSign(sign *stack, char e)
{	if (stack->top >= maximum)
		return;//栈满
	else
	{	stack->data[stack->top] = e;
		stack->top++;
	}
}

void PopSign(sign *stack, char *e)
{	if (stack->top == 0)
		return;
	else *e = stack->data[--stack->top];
}

void Calculate(number *stack, char e)// 计算结果
{	float num1, num2, result;
	PopNumber(stack, &num2);
	PopNumber(stack, &num1);
	switch (e)
	{	case '+':
			result = num1 + num2;
			PushNumber(stack, result);
			break;
		case '-':
			result = num1 - num2;
			PushNumber(stack, result);
			break;
		case '*':
			result = num1 * num2;
			PushNumber(stack, result);
			break;
		case '/':
			if (num2 == 0)
				printf("表达式错误！");
			else
			{	result = num1 / num2;
				PushNumber(stack, result);
				break;
			}
		case '^':
			result = pow(num1, num2);
			PushNumber(stack, result);
			break;
	}
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1816104.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

计算机视觉基础课程知识点总结

计算机视觉基础课程知识点总结

图像滤波 相关: 核与图像同向应用&#xff0c;不翻转。 卷积: 核在应用前翻转&#xff0c;广泛用于信号处理和深度学习&#xff08;现在常说的二维卷积就是相关&#xff09;。 内积: 向量化的点积操作&#xff0c;是相关和卷积的一部分。 模板匹配&#xff1a;通过在图像中…
阅读更多...
python数据分析-笔记本内存和价格预测分析

python数据分析-笔记本内存和价格预测分析

一、背景和研究意义 计算机已成为现代社会不可或缺的工具&#xff0c;广泛应用于个人生活、学术研究和商业领域。随着科学技术的飞速发展&#xff0c;计算机不仅在性能上不断突破&#xff0c;在种类和品牌上也呈现出多样化和差异化。无论是办公、娱乐、学习还是创作&#xff0…
阅读更多...
华为支持手指关节手势的原理

华为支持手指关节手势的原理

华为的指关节手势有指关节截屏、指关节录屏、指关节区域截屏、指关节分屏等。该技术的实现是靠触控结合了其他一些传感器实现的。 华为的专利&#xff1a; 一种手势控制方法、装置、终端设备和存储介质——华为技术有限公司 专利中提到以往终端设备对于手势的识别都是基于位置和…
阅读更多...
【机器学习300问】114、什么是度量学习？三元组损失又是什么？

【机器学习300问】114、什么是度量学习？三元组损失又是什么？

这些天都在加强自己的CV基本功&#xff0c;之前做过的人脸识别项目里有很多思考&#xff0c;在学习了这些基础知识后&#xff0c;我再次回顾了之前的人脸识别项目。我发现&#xff0c;很多之前困惑不解的问题现在都有了清晰的答案。 一、什么是度量学习&#xff1f; 度量学习也…
阅读更多...
vue相关的2个综合案例，网页打字练习

vue相关的2个综合案例，网页打字练习

for循环的应用 /* 1. 用for循环控制台打印0到100 */ for (var i 0; i < 100; i) {console.log(i) } /* 2. 用for循环控制台打印100到0 */ for (var i 100; i > 0; i--) {console.log(i) }网页打字练习案例练习 <template><div class"main"><…
阅读更多...
安灯（andon）系统如何帮助工厂流水线实现精益生产

安灯（andon）系统如何帮助工厂流水线实现精益生产

在当今竞争激烈的制造业领域&#xff0c;实现精益生产已成为众多工厂追求的目标。而安灯&#xff08;Andon&#xff09;系统在这一过程中发挥着至关重要的作用。 安灯&#xff08;Andon&#xff09;系统通过及时反馈和沟通机制&#xff0c;让生产过程中的问题能够迅速被察觉和解…
阅读更多...
【面向就业的Linux基础】从入门到熟练，探索Linux的秘密（二）

【面向就业的Linux基础】从入门到熟练，探索Linux的秘密（二）

主要内容介绍可tmux和vim的一些常用操作&#xff0c;可以当作笔记需要的时候进来查就行。 文章目录 前言 一、tmux和vim 二、Linux系统基本命令 1.tmux教程 2. vim教程 3.练习 总结 前言 主要内容介绍可tmux和vim的一些常用操作&#xff0c;可以当作笔记需要的时候进来查就行…
阅读更多...
清远mes系统开发商 盈致科技

清远mes系统开发商 盈致科技

清远MES系统开发商盈致科技为企业提供专业的MES系统解决方案&#xff0c;帮助企业实现生产过程的数字化管理和优化。盈致科技的服务范围包括但不限于以下方面&#xff1a;MES系统定制开发&#xff1a;盈致科技可以根据清远企业的实际需求定制开发适合的MES系统&#xff0c;满足…
阅读更多...
大神出新品，吴恩达开源机器翻译智能体项目

大神出新品，吴恩达开源机器翻译智能体项目

节前&#xff0c;我们星球组织了一场算法岗技术&面试讨论会&#xff0c;邀请了一些互联网大厂朋友、参加社招和校招面试的同学。 针对算法岗技术趋势、大模型落地项目经验分享、新手如何入门算法岗、该如何准备、面试常考点分享等热门话题进行了深入的讨论。 合集&#x…
阅读更多...
2 程序的灵魂—算法-2.4 怎样表示一个算法-2.4.2 用流程图表示算法

2 程序的灵魂—算法-2.4 怎样表示一个算法-2.4.2 用流程图表示算法

流程图表示算法&#xff0c;直观形象&#xff0c;易于理解。 【例 2.6】将例 2.1 求 5!的算用流程图表示。 【例 2.7】将例 2.2 的算用流程图表示。 【例 2.8】将例 2.3 判定闰年的算用流程图表示。
阅读更多...
双非本科一年20w，已是人中龙凤了

双非本科一年20w，已是人中龙凤了

大家好&#xff0c;我是白露啊。 “双非本科一年20w已经是人中龙凤了”……吗&#xff1f; 牛客上刷到这条帖子&#xff0c;我一开始以为是一个钓鱼、引战贴。看完才觉得他说的很对&#xff0c;现在在求职选择工作的时候&#xff0c;网上都觉得得40万、50万&#xff0c;但当真…
阅读更多...
SpringSecurity入门（一）

SpringSecurity入门（一）

1、引入依赖 spring-boot版本2.7.3&#xff0c;如未特殊说明版本默认使用此版本 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-security</artifactId></dependency><dependency><g…
阅读更多...
新书速览|Autodesk Inventor 2024入门与案例实战：视频教学版

新书速览|Autodesk Inventor 2024入门与案例实战：视频教学版

《Autodesk Inventor 2024入门与案例实战&#xff1a;视频教学版》 本书内容 《Autodesk Inventor 2024入门与案例实战&#xff1a;视频教学版》以Autodesk Inventor 2024为平台&#xff0c;重点介绍Autodesk Inventor 2024中文版的各种操作方法及其在工程设计领域的应用。《Au…
阅读更多...
TOGAF架构介绍

TOGAF架构介绍

框架组件 软件开发过程中通用能力的集合。 一个完整的框架包括&#xff1a;异常处理组件&#xff0c;数据访问组件&#xff0c;日志组件&#xff0c;错误码组件。
阅读更多...
韩顺平0基础学java——第21天

韩顺平0基础学java——第21天

p430-440 enum昨日剩余 enum常用方法&#xff1a; 1.toString已经重写过了&#xff0c;返回的是当前对象名。子类可以重写 2.name&#xff1a;返回当前对象名&#xff08;常量名&#xff09;&#xff0c;子类中不能重写 3.ordinal&#xff1a;返回当前对象的位置号。默认从…
阅读更多...
LVGL欢乐桌球游戏（LVGL+2D物理引擎学习案例）

LVGL欢乐桌球游戏（LVGL+2D物理引擎学习案例）

LVGL欢乐桌球游戏&#xff08;LVGL2D物理引擎学习案例&#xff09; 视频效果&#xff1a; https://www.bilibili.com/video/BV1if421X7DL
阅读更多...
webshell获取总结（cms获取方法、非cms获取方法、中间件拿Webshell方法）

webshell获取总结（cms获取方法、非cms获取方法、中间件拿Webshell方法）

目录 前期准备&#xff1a; 1、cookices靶场网站搭建&#xff1a; 2、dedecms靶场环境搭建&#xff1a; 获取Webshell方法总结&#xff1a; 一、CMS获取Webshell方法 二、非CMS获取Webshell方法 1、数据库备份获取Webshell 例如&#xff1a; 2、抓包上传获取Webshell 3、…
阅读更多...
SPI 配置寄存器程序

SPI 配置寄存器程序

/************************************************** * **************************************************/ module zhm_mspi #( parameter C_SPI_CPHA 1 ,// clock phase &#xff0c;0&#xff0c;在 SCLK 的第一个跳变沿进行采样&#xff1b;1&…
阅读更多...
Linux - 复盘一次句柄数引发的故障

Linux - 复盘一次句柄数引发的故障

文章目录 Pre&#xff08;内核、用户、进程&#xff09;句柄数设置问题 shell修复 Pre Linux - 深入理解/proc虚拟文件系统&#xff1a;从基础到高级 &#xff08;内核、用户、进程&#xff09;句柄数设置 在Linux系统中&#xff0c;进程打开的最大句柄数可以通过多种方式配置…
阅读更多...
0605 实际集成运算放大器的主要参数和对应用电路的影响

0605 实际集成运算放大器的主要参数和对应用电路的影响

6.5.1 实际集成运放的主要参数 6.5.2 集成运放应用中的实际问题 6.5.2 集成运放应用中的实际问题
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023