前言 动态规划模型从尝试暴力递归到傻缓存到动态规划

四种模型和体系班两种模型一共六种模型

0.1 从左往右模型

0.2 范围讨论模型范围尝试模型 （这种模型特别在乎讨论开头如何如何 结尾如何如何）

玩家博弈问题，玩家玩纸牌只能那左或者右

0.3 样本对应样本对应模型（特别在乎两个样本结尾如何如何 最长公共子序列）

0.4 业务限制模型

动态规划只是暴力尝试的一个缓存
 

1.2 分析

到当前货物的时候有两种选择，要么选择当前货物，要么不选择当前货物

base 条件的判断分析

if (rest < 0) {

return -1;}

这里为什么不能取return 0，因为上由传下来的剩下的bags的重量要大于0上由的值才是有意义的；

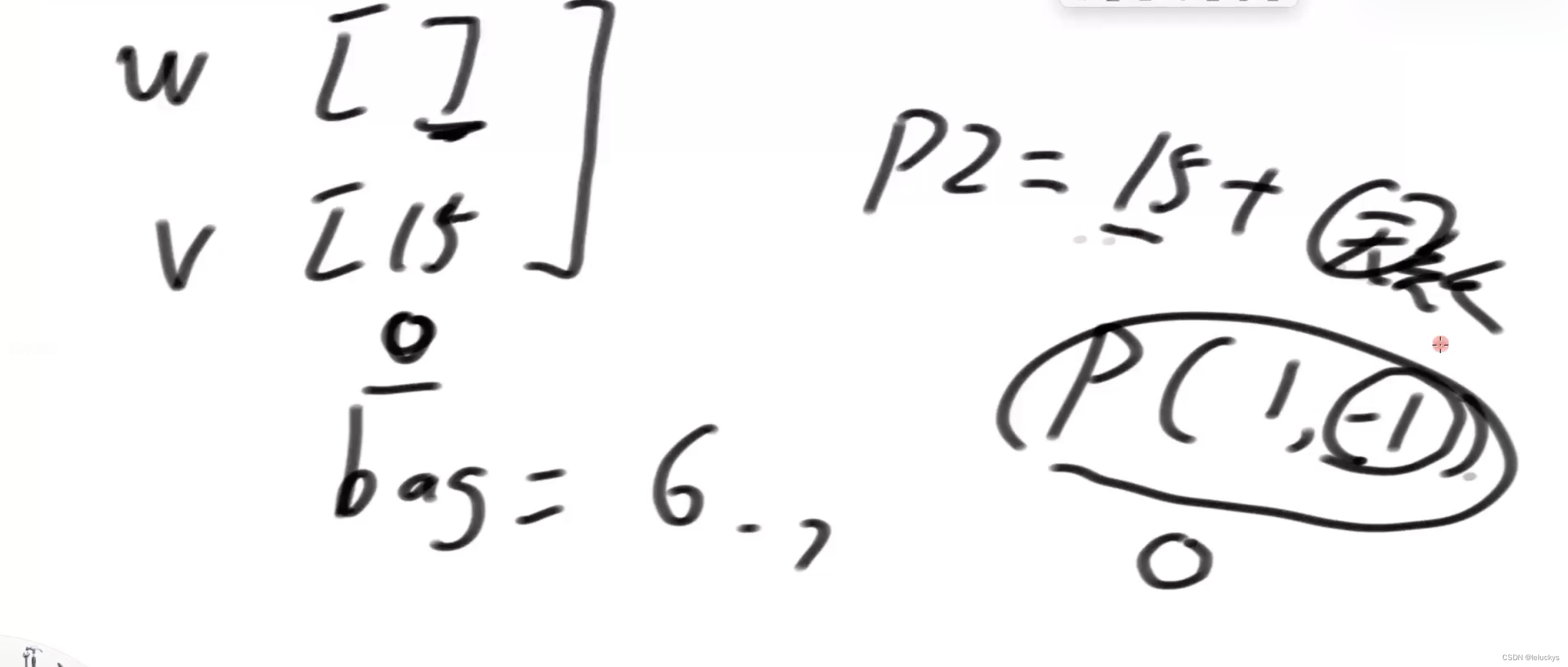
递归改动态规划

第一步找确定的值

if (index == w.length) {

return 0;

}

第二步找动态的值喝确定值之间的关系，动态的值时如何根据静态值退出来的

int p1 = process(w, v, index + 1, rest);

int next = process(w, v, index + 1, rest - w[index]);

这辆动态函数都需要依赖他的一行，最后一行又是确定值

1.3 尝试递归代码

// 所有的货，重量和价值，都在w和v数组里
    // 为了方便，其中没有负数
    // bag背包容量，不能超过这个载重
    // 返回：不超重的情况下，能够得到的最大价值
    public static int maxValue(int[] w, int[] v, int bag) {
        if (w == null || v == null || w.length != v.length || w.length == 0) {
            return 0;
        }
        // 尝试函数！
        return process(w, v, 0, bag);
    }

    // index 0~N
    // rest 负~bag
    public static int process(int[] w, int[] v, int index, int rest) {
        if (rest < 0) {
            return -1;
        }
        if (index == w.length) {
            return 0;
        }
        //不选择当前的货物
        int p1 = process(w, v, index + 1, rest);
        int p2 = 0;
        //要选择当前的货物
        int next = process(w, v, index + 1, rest - w[index]);
        if (next != -1) {
            p2 = v[index] + next;
        }
        return Math.max(p1, p2);
    }

1.4 改动态规划

递归改动态规划

第一步找确定的值

第二步找动态的值喝确定值之间的关系，动态的值时如何根据静态值退出来的

改动态规划 看是否有重复的情况

下面的p（3，10）都会重复

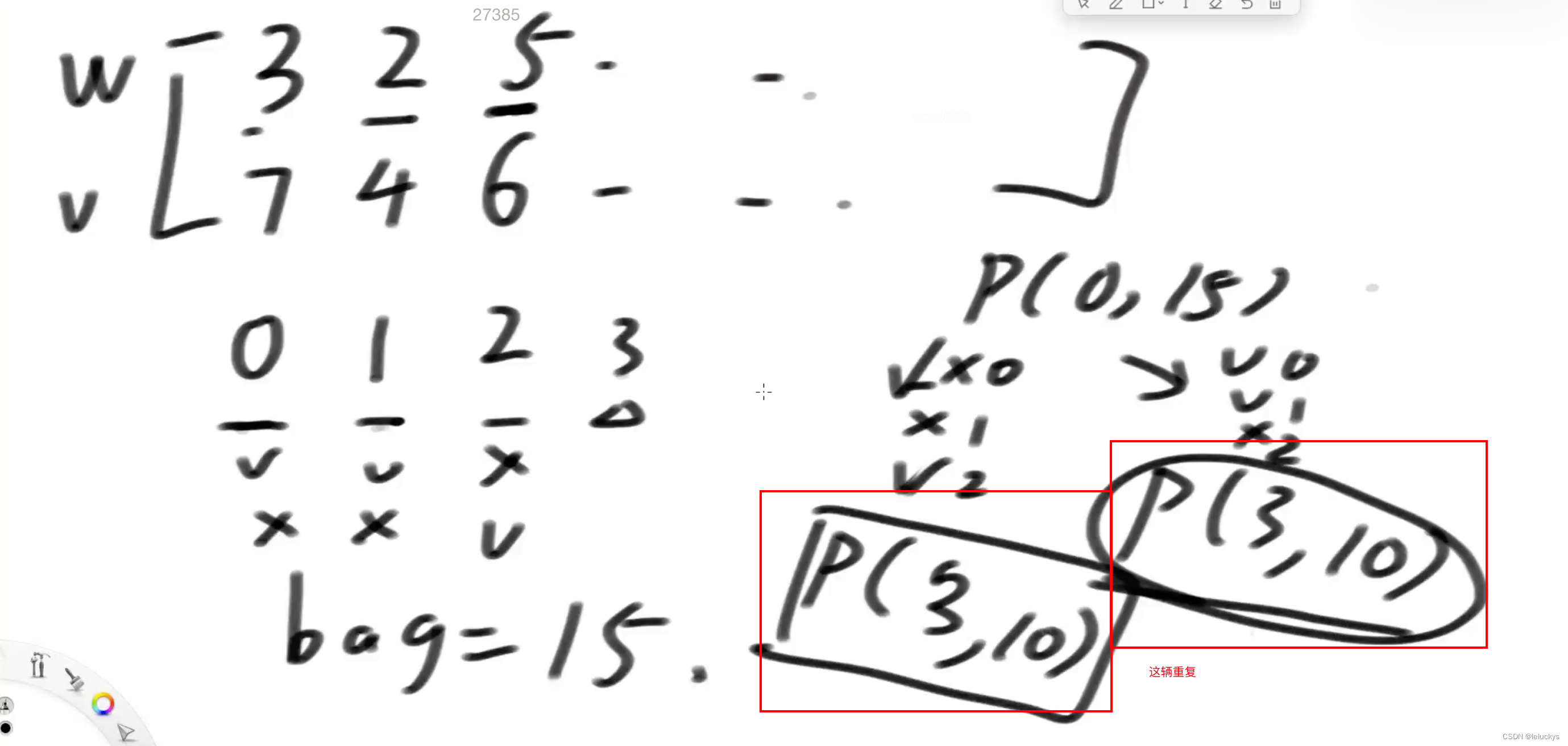
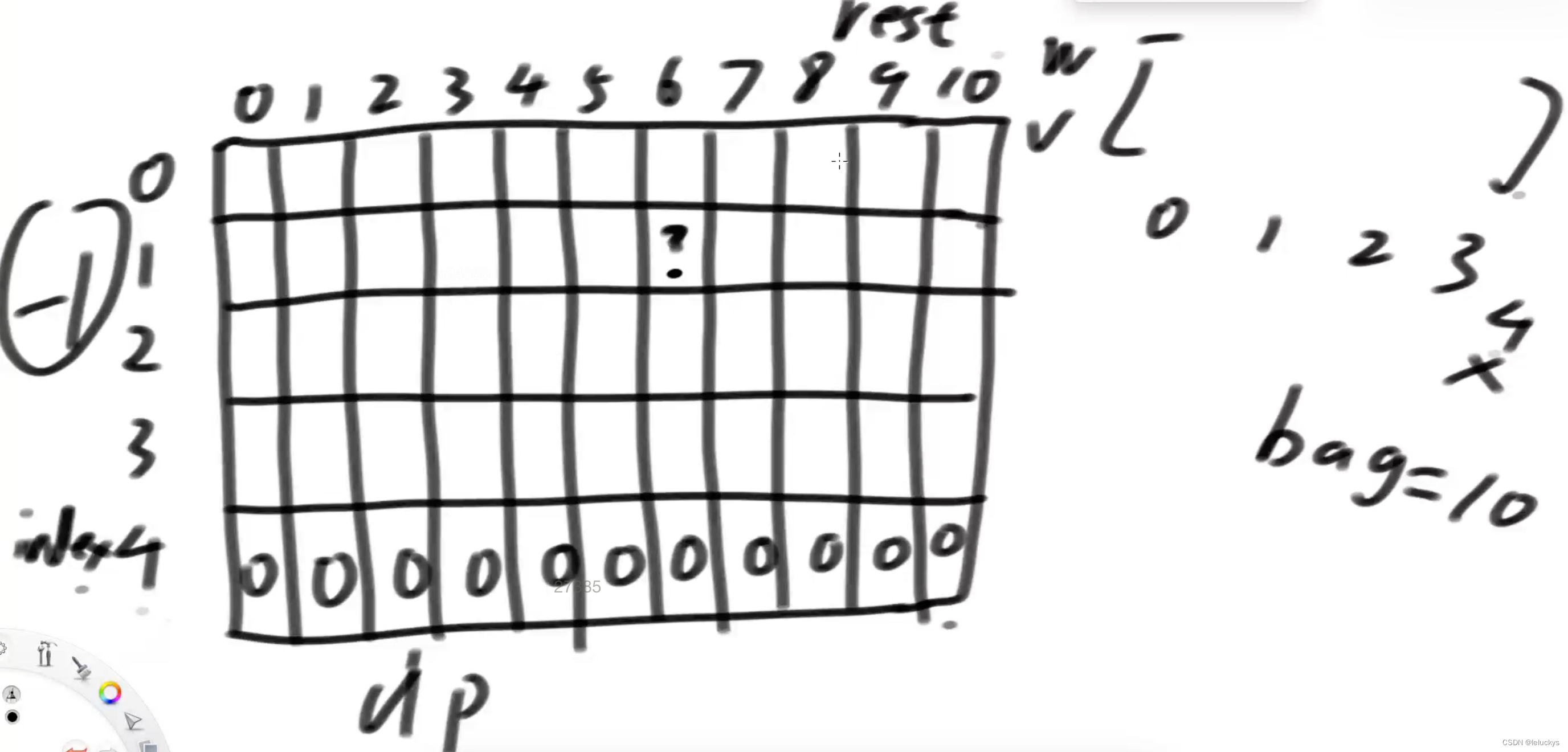
1.5 动态规划代码

public static int dp(int[] w, int[] v, int bag) {
        if (w == null || v == null || w.length != v.length || w.length == 0) {
            return 0;
        }
        int N = w.length;
        int[][] dp = new int[N + 1][bag + 1];
        for (int index = N - 1; index >= 0; index--) {
            for (int rest = 0; rest <= bag; rest++) {
                int p1 = dp[index + 1][rest];
                int p2 = 0;
                int next = rest - w[index] < 0 ? -1 : dp[index + 1][rest - w[index]];
                if (next != -1) {
                    p2 = v[index] + next;
                }
                dp[index][rest] = Math.max(p1, p2);
            }
        }
        return dp[0][bag];
    }

    public static void main(String[] args) {
        int[] weights = { 3, 2, 4, 7, 3, 1, 7 };
        int[] values = { 5, 6, 3, 19, 12, 4, 2 };
        int bag = 15;
        System.out.println(maxValue(weights, values, bag));
        System.out.println(dp(weights, values, bag));
    }

}