# -*- coding: utf-8 -*-
"""
Created on Fri May 24 09:04:23 2024


"""

import os
import sys
import math
import heapq
import matplotlib.pyplot as plt
import time

'''
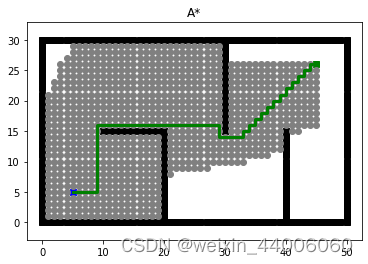
传统A*算法
'''


class Astar:
    '''
    AStar set the cost + heuristics as the priority
    AStar将成本+启发式设置为优先级
    '''

    def __init__(self, s_start, s_goal, heuristic_type, xI, xG):
        self.s_start = s_start
        self.s_goal = s_goal
        self.heuristic_type = heuristic_type
        self.u_set = [(-1, 0), (0, 1), (1, 0), (0, -1)]

        # self.obs = self.obs_map()  # 障碍物位置
        self.Open = []  # 优先级序列，open集合
        self.Closed = []  # 相邻点集合，访问visited序列
        self.parent = dict()  # 相邻父节点
        self.g = dict()  # 成本
        self.x_range = 51  # 设置背景大小
        self.y_range = 51

        self.xI, self.xG = xI, xG
        self.obs = self.obs_map()

    def animation(self, path_l, visited_l, name, path_color='g'):

        # 绘制地图基础元素
        obs_x = [x[0] for x in self.obs]
        obs_y = [x[1] for x in self.obs]
        plt.plot(self.xI[0], self.xI[1], "bs")  # 起点
        plt.plot(self.xG[0], self.xG[1], "gs")  # 终点
        plt.plot(obs_x, obs_y, "sk")  # 障碍物
        plt.title(name)
        plt.axis("equal")

        # 移除起点和终点于visited_l列表中，避免它们被标记为已访问点
        visited_l = [node for node in visited_l if node != self.xI and node != self.xG]

        # 绘制所有已访问节点
        for x in visited_l:
            plt.plot(x[0], x[1], color='gray', marker='o')

        # 绘制路径
        path_x = [point[0] for point in path_l]
        path_y = [point[1] for point in path_l]
        plt.plot(path_x, path_y, linewidth=3, color=path_color)

        # 显示最终图形
        plt.show(block=True)

    def obs_map(self):
        """
        Initialize obstacles' positions
        :return: map of obstacles
        初始化障碍物位置
        返回：障碍物
        """
        x = 51
        y = 31
        self.obs = set()

        # 绘制边界
        self.obs.update((i, 0) for i in range(x))

        self.obs.update((i, y - 1) for i in range(x))

        self.obs.update((0, i) for i in range(y))

        self.obs.update((x - 1, i) for i in range(y))

        # 给出障碍物坐标集1
        self.obs.update((i, 15) for i in range(10, 21))
        self.obs.update((20, i) for i in range(15))

        # 给出障碍物坐标集2
        self.obs.update((30, i) for i in range(15, 30))

        # 给出障碍物坐标集3
        self.obs.update((40, i) for i in range(16))

        return self.obs

    def searching(self):
        """
        A_star Searching.
        :return: path, visited order

        Astart搜索，返回路径、访问集，
        """

        self.parent[self.s_start] = self.s_start  # 初始化 起始父节点中只有起点。
        self.g[self.s_start] = 0  # 初始代价为0
        self.g[self.s_goal] = math.inf  # 目标节点代价为无穷大

        # 将元素(self.f_value(self.s_start), self.s_start)插入到Open堆中，
        # 并保持堆的性质（最小堆中父节点的值总是小于或等于其子节点的值））
        # 这行代码的意思是：计算起始节点s_start的评估值f_value(self.s_start)，
        # 然后将这对值(f_value, self.s_start)作为一个元组插入到self.Open这个最小堆中。
        # 这样做的目的是在诸如A*搜索算法等需要高效管理待探索节点的场景下，
        # 确保每次可以从堆顶（也就是当前评估值最小的节点）取出下一个待处理的节点。
        # 这对于寻找最短路径、最小成本解决方案等问题非常有用。
        heapq.heappush(self.Open, (self.f_value(self.s_start), self.s_start))

        while self.Open:
            # heappop会取出栈顶元素并将原始数据从堆栈中删除
            # 在这个例子中，heappop返回的元素假设是一个包含两个元素的元组，
            # 但代码中只关心第二个元素（实际的数据，比如一个状态、节点或其他任何类型的数据），
            # 所以用_占位符丢弃了第一个元素（通常是评估值或优先级），而把第二个元素赋值给了变量s
            _, s_current = heapq.heappop(self.Open)  # s_current存储的是当前位置的坐标
            # print('栈顶元素为{0}'.format(s_current))

            self.Closed.append(s_current)

            if s_current == self.s_goal:  # 迭代停止条件，判断出栈顶元素是否为目标点，如果为目标点，则退出
                break
            # 如果不是，更新该点附近的代价值
            # get_neighbor为获取附近点的坐标
            for s_next in self.get_neighbor(s_current):
                new_cost = self.g[s_current] + self.cost(s_current, s_next)

                if s_next not in self.g:
                    self.g[s_next] = math.inf

                if new_cost < self.g[s_next]:
                    self.g[s_next] = new_cost
                    self.parent[s_next] = s_current
                    # heappush入栈时需要存储的该点的代价值的计算方式为
                    heapq.heappush(self.Open, (self.f_value(s_next), s_next))

        # self.animation(self.extract_path(self.parent), self.Closed, "A*")
        return self.extract_path(self.parent), self.Closed

    def get_neighbor(self, s_current):
        """

        :param s_current:
        :return: 相邻点集合
        """
        return [(s_current[0] + u[0], s_current[1] + u[1]) for u in self.u_set]

    def cost(self, s_current, s_next):
        """
        :param s_current 表示当前点
        :param s_next 表示相邻点
        :return 若与障碍物无冲突，则范围欧式距离成本，否则为无穷大成本
        计算当前点与相邻点的距离成本
        """
        # 判断是否与障碍物冲突
        if self.is_collision(s_current, s_next):
            return math.inf
        # 这里返回欧式距离成本
        return math.hypot(s_next[0] - s_current[0], s_next[1] - s_current[1])

    def is_collision(self, s_current, s_next):
        """
            check if the line segment (s_start, s_end) is collision.
            :param s_current: start node
            :param s_next: end node
            :return: True: is collision / False: not collision
            检查起终点线段与障碍物是否冲突
        如果线段的起点或终点之一位于障碍物集合 self.obs 内，则直接判定为碰撞，返回 True。
        若线段不垂直也不水平（即斜线段），则分为两种情况检查：
            若线段为45度线（斜率为1:1或-1），则检查线段的端点形成的矩形框内是否有障碍物。
            否则检查线段端点形成的另一矩形框内是否有障碍物。
        若上述任一矩形框内有障碍，则判定为碰撞，返回 True
        若无碰撞情况，则返回 False
        """
        # obs是障碍物，如果遇到障碍物，则距离（成本）无穷大
        if s_current in self.obs or s_next in self.obs:
            return True
        ''''''
        # 如果该点s_start与相邻点s_end不相同
        if s_current[0] != s_next[0] and s_current[1] != s_next[1]:

            # 如果两点横纵坐标之差相等,即线段不垂直也不水平。135度线
            if s_next[0] - s_current[0] == s_current[1] - s_next[1]:
                s1 = (min(s_current[0], s_next[0]), min(s_current[1], s_next[1]))

                s2 = (max(s_current[0], s_next[0]), max(s_current[1], s_next[1]))
            # 如果两点横纵坐标之差不相等
            else:
                s1 = (min(s_current[0], s_next[0]), max(s_current[1], s_next[1]))
                s2 = (max(s_current[0], s_next[0]), min(s_current[1], s_next[1]))
            # obs是障碍物
            if s1 in self.obs or s2 in self.obs:
                return True
        return False

    def f_value(self, s_currrent):
        """
        f = g + h. (g: Cost to come, h: heuristic value)
        :param s: current state
        :return: f
        """

        return self.g[s_currrent] + self.heuristic(s_currrent)

    def extract_path(self, parent):

        path = [self.s_goal]
        s = self.s_goal

        while True:
            s = parent[s]
            path.append(s)

            if s == self.s_start:
                break

        return list(path)

    def heuristic(self, s_current):

        heuristic_type = self.heuristic_type  # heuristic type
        goal = self.s_goal  # goal node
        # 如果为manhattan，则采用曼哈顿距离，s存储的是中间点
        if heuristic_type == "manhattan":
            return abs(goal[0] - s_current[0]) + abs(goal[1] - s_current[1])
        # 否则就是欧几里得距离，符合勾股定理
        else:
            return math.hypot(goal[0] - s_current[0], goal[1] - s_current[1])


if __name__ == '__main__':
    time_start = time.time()
    s_start = (5, 5)
    s_goal = (45, 26)

    star_m = Astar(s_start, s_goal, "ee", s_start, s_goal)

    path, visited = star_m.searching()
    star_m.animation(path, visited, "A*")  # animation
    time_end = time.time()
    print("程序运行时间：", time_end - time_start)