算法导论实战（七）（山东大学软件学院算法历年考题+朋辈辅导）

🌈 个人主页：十二月的猫-CSDN博客
🔥 系列专栏： 🏀算法启示录

💪🏻 十二月的寒冬阻挡不了春天的脚步，十二点的黑夜遮蔽不住黎明的曙光

前言

第一周

题目一

题目二

题目三

题目四

第二周

题目一

题目二

题目三

题目四

第三周

题目一

题目二

题目三

题目四

题目五

题目六

第四周

题目一

题目二

题目三

题目四

题目五

第五周

题目一

题目二

题目三

题目四

第六周

题目一

题目二

题目三

题目四

题目五

题目六

总结

前言

算法导论的知识点学习将持续性更新在算法启示录_十二月的猫的博客-CSDN博客，欢迎大家订阅呀（反正是免费的哦~~）

实战篇也将在专栏上持续更新，主要目的是强化对理论的学习（题目来源：山东大学孔凡玉老师推荐）

第一周

题目一

问题描述：

问题求解：

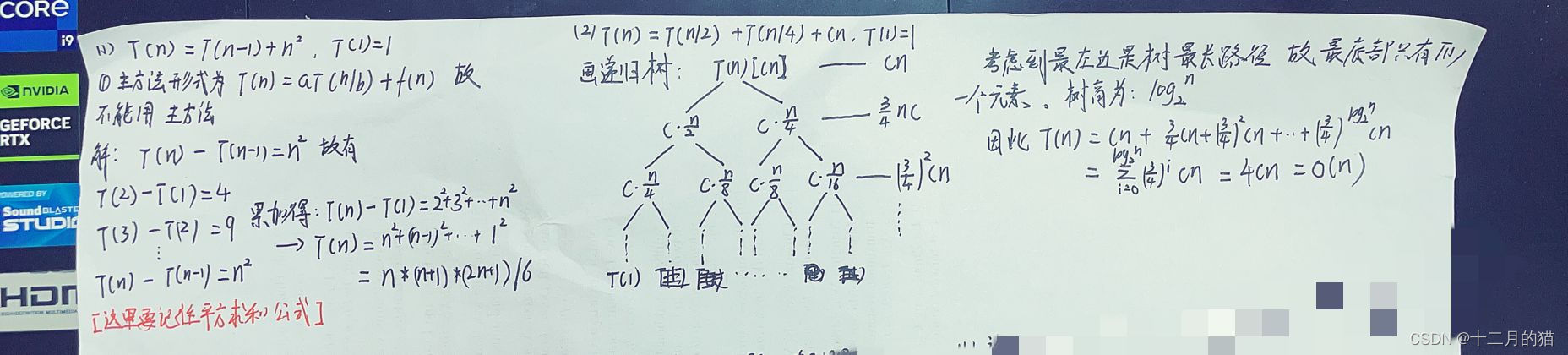
关键点：

1、主方法的使用存在条件，不满足条件不能使用。同时使用主方法时要注意需要在多项式时间上大于或小于

举个反例：nlgn和n，因为nlgn/n=lgn，而lgn无论e取多小n^e永远大于lgn，所以nlgn并不是多项式时间上大于n的

2、递归树可能存在只有一条路径能走到最底部的情况，但是此时上文发现的等比/等差规律是相同的

3、树叶子结点： $nlog^a_b$

树高： $log_b^n$

题目二

问题描述：

问题求解：

有了上面的get_max函数后，可以写出程序如下：

FIND_MAX_SUBARRAY(A,low,high)
    if low==high
        return A[low]
    else 
        mid=(low+high)/2
        (left_start,left_end,left_sum)=FIND_MAX_SUBARRAY(A,low,mid)
        (right_start,right_end,right_sum)=FIND_MAX_SUBARRAY(A,mid+1,high)
        (cross_start,cross_end,cross_sum)=get_max(A,mid,low,high)
        if left_sum>=right_sum and left_sum>=cross_sum
            return (left_start,left_end,left_sum)
        else if right_sum>left_sum and right_sum>cross_sum
            return (right_start,right_end,right_sum)
        else
            return (cross_start,cross_end,cross_sum)

题目三

问题描述：

问题求解：

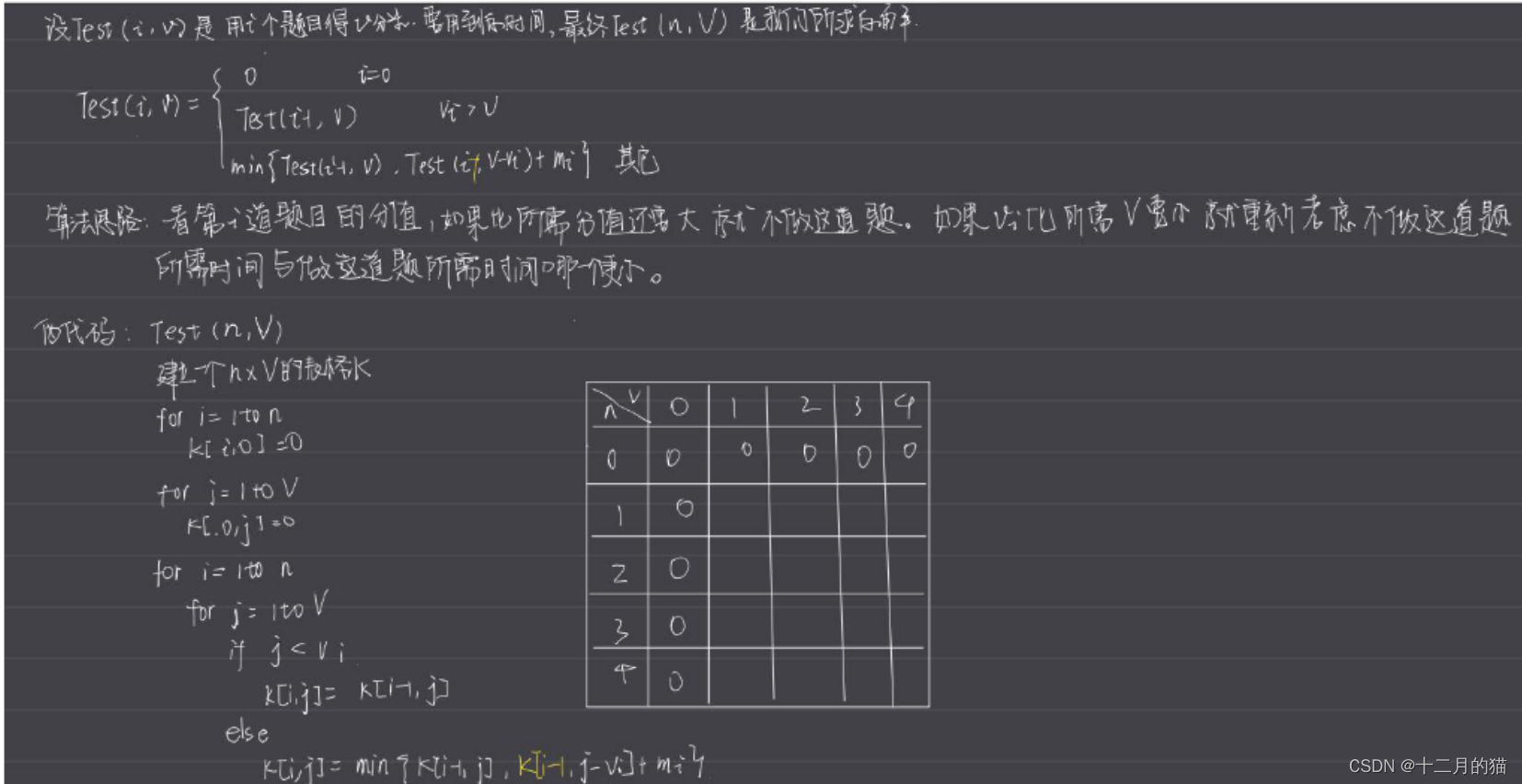
注意：这里当i=0时，代表没有题目，此时的Test（0，j）=+∞表示该要求不可能完成（上面解答这个地方是错误的！！）

题目四

问题描述：

问题求解：

证明上面贪心算法是正确的：

第二周

题目一

问题描述：

问题求解：

贪心证明的关键点：

1、明确贪心准则

2、明确在贪心准则下做出的贪心策略

3、利用替换法，用贪心策略替换全局最优解中的部分子问题，从而得到新的全局最优解

4、通过1-3证明局部最优就是全局最优

题目二

问题描述：

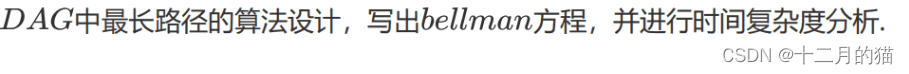
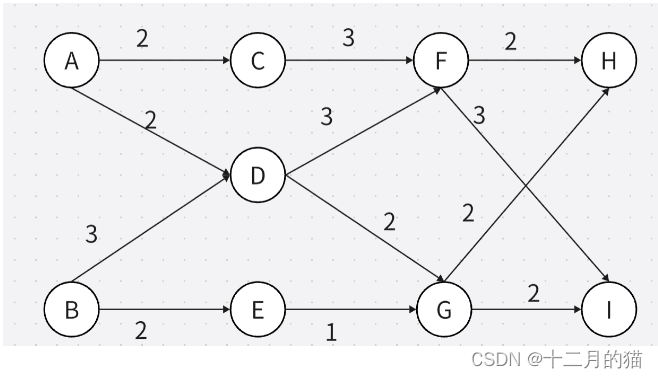
问题求解：

关键点：

1、简单有向图的最短路径是可以通过动态规划求解的，但是简单有向图的最长路径不能通过动态规划求解。因为动态规划要求有最优子结构和重叠子问题，但是简单有向图由于可能有环路，所以最长路径是无法求解的，但是在DAG（简单无环路有向图）中最长路径最短路径都是可以用动态规划求解的

2、bellman方程就是动态转移方程

3、图最长路径=max{图中各点最长路径}，也就是图中各点最长路径中的最大值

题目三

问题描述：

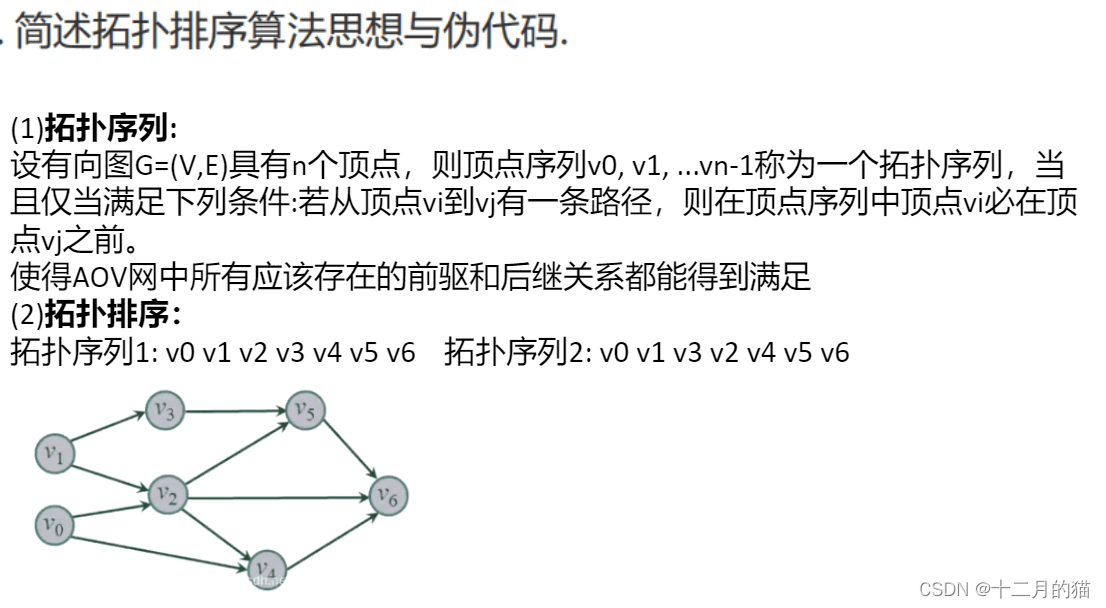
问题求解：

关键点：

1、拓扑排序的生成方式有DFS、Kanh算法两个；两个算法的适用条件基本是类似的，都是DAG（简单有向无环图）

2、理解DFS、BFS算法：DFS算法特点是尽量深入，也就是说算法会深入到不可以再深入再去输出值；BFS算法特点是尽量宽广，也就是说算法是找到一个点就输出，然后找下一层再去输出，一层一层地输出

3、本题求解阐述的是Kanh算法

4、拓扑排序和其他排序算法类似，都是对数据的处理。只不过这里的数据指的是图数据和传统数字数据有一点不同（拓扑排序可以用来求解结点的路径数）

题目四

问题描述：

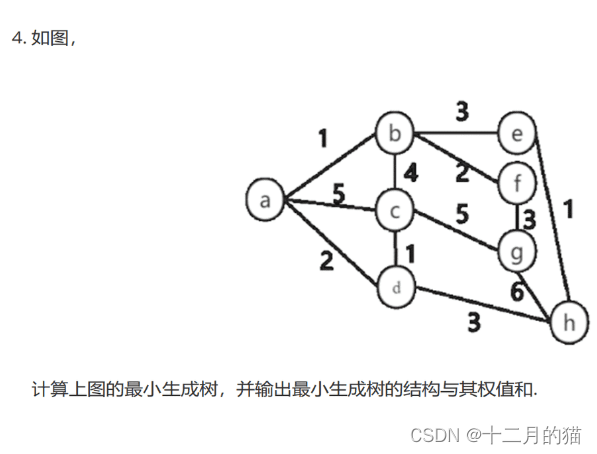
问题求解：

关键点：

1、进一步思考这两个算法的时间复杂度：

Kruskal算法：O（ElogE）

Prim算法：O（VlogV+ElogV）=O（ElogV）

2、两个方法都可以通过维护最小二叉树来完成提取最小值

第三周

题目一

问题描述：

Floyd - Warshall算法，简述算法思想，分析时间复杂度。

问题求解：

关键点：

1、我个人不喜欢动态规划转移方程用这种方式书写，我认为这种方式是避开了转移的本质以及可解释性。但是好处是它对于代码书写非常方便，因为直接写成代码的格式。

2、状态转移方程应该如下： $d_{ij}^k=min\{d_{ij}^{k-1},d_{ik}^{k-1}+d_{kj}^{k-1}\}$

3、理解这个状态转移方程需要深刻理解k变量的含义：k表示从i到j点经过{1,2,3....k}中的点

但是转化到代码中：k表示转移的趟数，即递归的深度/次数（目前这一轮的结果依赖前一轮的结果，这也是递归的本质体现）

4、有前面的理解很自然能将 $d_{ij}^k$ 写成三层嵌套循环：第一层k表示递归深度，第二层第三层表示哪两个点之间的距离

题目二

问题描述：

问题求解：

关键点：

1、最常用的解决问题思想：动态规划思想、贪心思想。本题求解的是个数，个数显然是没有贪心策略去反复求解的。那么最直接的就是通过动态规划，建立子问题和原问题之间的转移方程去解决

2、对于字符串问题，最常用的方法就是把注意力放到字符串的结尾，对结尾的数进行分类去递归

3、本题就是对末尾数是a和不是a进行分类讨论，具体分类见上图的解法，本题的解法与爬楼梯问题相当类似，建议有空的友友去看看

题目三

问题描述：

问题求解：

关键点：

1、本题的动态转移方程和前面的都不同：这个动态方程表示的两个转移方式是有前提条件的，转移方式受到前提条件的影响

2、所以在使用动态转移方程时需要对条件进行分类：ifelse

题目四

问题描述：

问题求解：

关键点：

1、本题更像题目二和题目三特点的混合体：本题是字符串题，所以重点在于比对字符串结尾的字符来分类判断转移方式；同时本题在比对字符串结尾字符后对不同的转移方式要进行分类，这个分类就是题目三的类型，多转移类型

题目五

问题描述：

问题求解：

关键点：

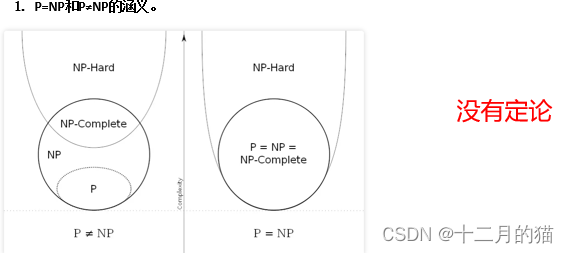
1、 NP-hard问题：至少和NP一样困难，表示NP-hard不一定是NP问题，但是NP-hard和NP的交集就是NPC问题。NP-hard问题满足NPC问题的第二个定义（其他NP问题能够归约到这个问题），不满足第一个定义（是NP问题）

题目六

问题描述：

问题求解：

关键点：
1、本题要利用贝尔曼福特算法的变型来处理。贝尔曼福特算法正确性在于三角形理论的数学基础，如果我们修改其松弛条件，那么便不满足三角形理论了

2、三角形理论保证贝尔曼算法在第v轮松弛时能够使得v长度的最短路径的点都得到正确路径长度，从而在下一轮松弛时v+1长度的最短路径点能够利用v长度路径点得到其正确结果

3、最长路径不再满足三角形理论，所以需要提前用拓扑排序对所有点进行排序，保证后一个点执行时，前一个点已经得到它的最长路径

最长路径、路径数都需要用到拓扑排序

第四周

题目一

问题描述：

问题求解：

关键点：

1、saturated edge：饱和边

2、augmenting path：增广路径

题目二

问题描述：

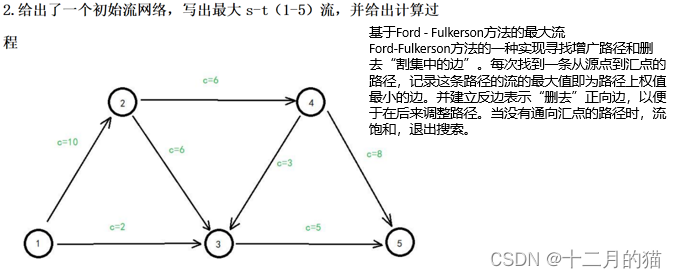
问题求解：

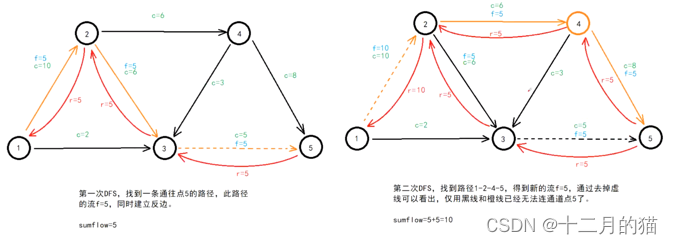
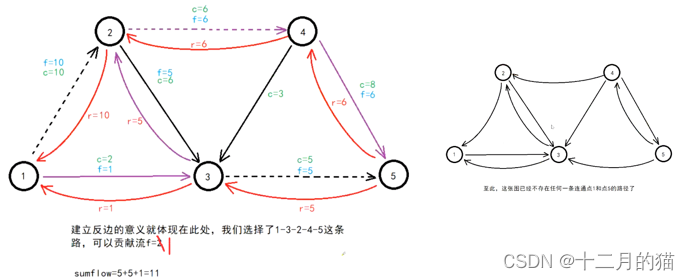
关键点：

1、建立残存网络后利用DFS去找增广路径。DFS找增广路径有两个要点：a.在两个路都可以走的前提下优先找流大的增广路径；b.在多个路之间流容量都相等的情况下，优先选择数字小的那个点

题目三

问题描述：

证明对于可行流的任意一个割，割的流量=可行流的流量

问题求解：

采用归纳法来求解。设可行流的源点为S，汇点为T，构造一个割（{S‘}，{T}），割的左边有除了T以外的所有点，右边只有汇点T。此时割的流量就是汇入汇点T的流量之和，也就是可行流的流量，证明成立。

其他割可以通过给（T）增加点来实现，令目前向（T）中增加一个点V，那么新的割的流量会减少由V向（T）中所有点的流量，同时加上由（S’）中所有其他点流向V的流量，根据V点的流量守恒定理可以确定割减少的流量和增加的流量是相等的。所以割的流量是不会改变的，即所有割的流量=割（{S‘}，{T}）=可行流流量

题目四

问题描述：

问题求解：

证明：

1→2：利用反证法，假设1不能推导出2，也就是说存在一个割（A，B），有cap(A，B）=val（f），但是f不是最大流。因为f不是最大流，因此存在一个流f’>f，即有val(f')>val(f)=cap（A，B），但是根据已知定理任何流的值都要小于等于网络图中任意割的值，故与此时的假设矛盾，假设不成立

2→3：利用逆否命题——存在一个增广路径->f不是最大流。再利用反证法，证明存在一个增广路径，可以推导出f是最大流是错误的。假设存在一个增广路径，那么对于增广路径P，其每条路径上的前向路可以增加流量，后向路可以减少流量，但是这两个措施都会导致流量最终变大，因此f不是最大流

3→1：在图G的残存网络Gf中没有任何增广路径，那么就代表G中从源点到汇点的路径中如果存在（u,v)那么这个边的值一定是c(u,v)即饱和边，如果存在（v，u）那么这个边的值一定等于0。将从源点S能到达点组合成一个集合S0，剩下的点组合成一个集合T0。对于这个割而言，S0到T0之间的路一定都是饱和前向路或者零流后向路，因此割的流量=前向路流量-后向路流量=前向路流量-0=割的容量，又因为割的流量此时就是图的可行流流量，所以有val(f)=cap(A，B）成立

题目五

问题描述：

解释“归约”的概念并证明顶点覆盖归约到集合覆盖

问题求解：

归约是指：

将一个问题转化为另一个问题的过程，使得一个问题的算法可以用于另一个问题的解决。如果一个问题A可以归约为另一个问题B，并且这个归约是多项式时间的，那么我们可以说问题B的算法可以直接用来解决问题A，问题A的算法也可以用于解决问题B

证明集合覆盖是一个NPC问题：

1、假如在集合覆盖问题中，给定一个集合覆盖集，即集合S1、S2、S3能够覆盖集合U。那么只要遍历U中的元素看是否都能在S1、S2、S3集合中找到，就可以验证这个结果。同时直接求解U的子集合覆盖是不能在多项式时间内解决的，所以可以证明集合覆盖问题是NP问题

2、选择顶点覆盖问题用来归约

3、假设存在一个图有(a0,a1,a2,...,ak)个顶点，其中顶点覆盖集有（a2,a3,a5,...)。此时将图G的所有边记录成（e1,e2,...,en)并将这个边集表示为集合U，再将顶点覆盖集中的每个顶点所连接的边都创建为一个集合（例如顶点a2连接的边创建为集合S2），假如顶点覆盖集能够覆盖图G的所有边，那么新创建的集合的并集也一定能够覆盖集合U，并且这个顶点集是最小的，则这个子集合数也将是最小的

4、假如存在一个集合覆盖，那么将集合覆盖的子集转化为点和其对应的边，将全集U转化为图G的所有边，那么一定存在一个顶点覆盖问题的解与其对应。所以这两个问题的归化是当且仅当的关系

5、可以证明这个归约算法只要将顶点连接的边创建为集合，即可完成从顶点覆盖到集合覆盖的归约。所以这个归约算法是多项式时间内的

第五周

题目一

题目二

问题描述：

问题求解：

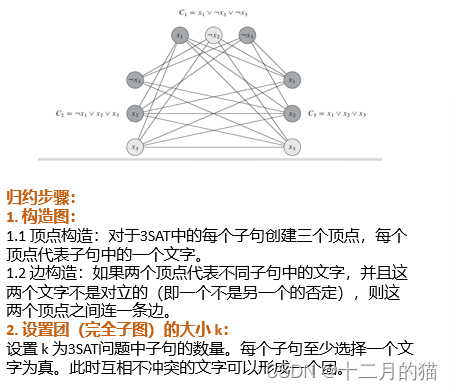
归约正确性证明：

题目三

问题描述：

问题求解：

归约正确性证明：

题目四

问题描述：

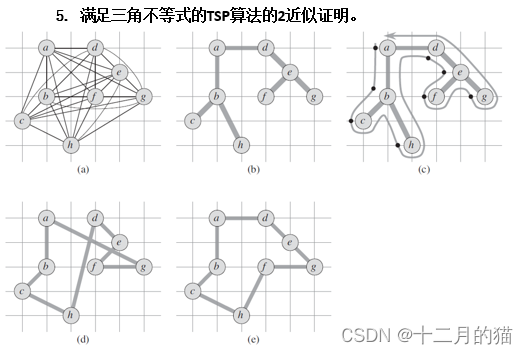
问题求解：

1、构建最小生成树：从给定的完全图 G 中找到最小生成树 T。

2、双倍遍历写出初始路径：从任意顶点开始对最小生成树 T 进行深度优先搜索（DFS）或其他遍历方式，确保每条边遍历两次（来回走），这样形成的路径记为 W。（c(W)≤2c(T)）

3、简化路径 W：将 W 中重复访问的顶点删除，只保留第一次访问的情况，形成哈密顿回路 H。(c(H)≤c(W))，c(H)>c(T)

简化路径步骤正确性证明：

短路步骤和三角不等式：

短路步骤不会增加总路径长度，由于满足三角不等式，直接从一个城市到另一个城市的距离不会超过通过其他城市间接到达的距离。因此，跳过已访问城市只会减少总距离或保持不变。

第六周

题目一

问题描述：

问题求解：

关键点：

1、本题是用贪心思想来解决。总结贪心常用的地方：线段覆盖、集合覆盖、活动选择、教室分配、短时间作业

2、本题需要在满足覆盖start的前提下，仅可以选择覆盖最远的地方。所以需要先进行排序

题目二

问题描述：

问题求解：

算法思想：

该问题可以使用动态规划来解决。我们可以定义一个二维数组dp，其中dp[i][j]表示合并第i堆到第j堆砖所需的最小代价。然后，我们可以使用递推关系式来计算dp[i][j]的值。假设k为i到j之间的一个划分点，那么dp[i][j]的值可以通过尝试所有可能的划分点k来得到，即dp[i][j] = min(dp[i][k] +dp[k+1][j] + sum[i][j])，其中sum[i][j]表示第i堆到第j堆砖的总块数之和。

最后，我们可以通过填充dp数组并返回dp[1][n]来得到最小合并代价。

代码实现：

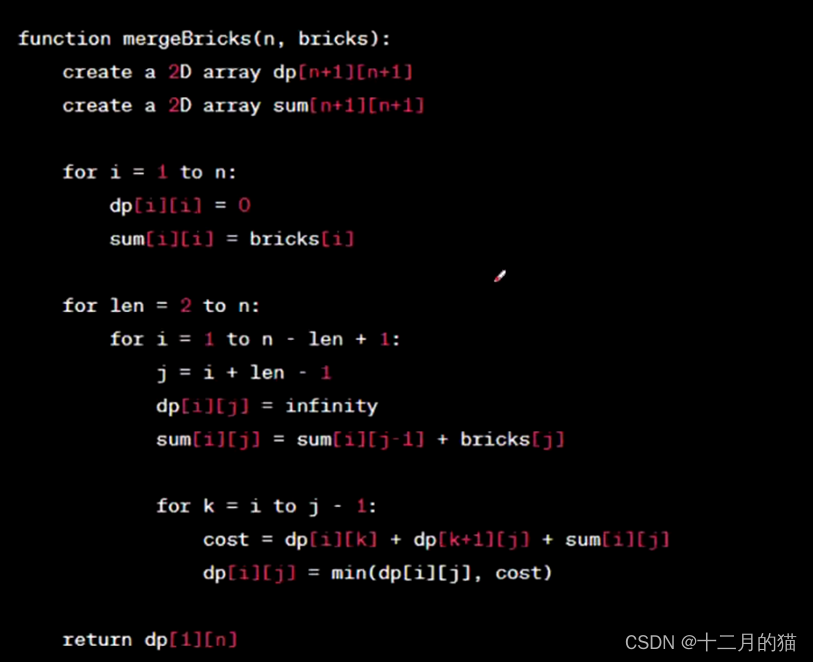
关键点：

合并代价sum[i][j]函数也需要通过递归方法，利用子问题来求解

题目三

问题描述：

问题求解：

（1）递推关系式：

在该问题中，我们可以使用以下递推关系式来计算dp数组的值：

dp[i][j] = max(dp[i-1][j], dp[i][j-1]) + a[i][j]

其中，dp[i][j]表示从左上角a[0][0]走到当前格子a[i][j]时能够捡到宝贝的最大价值之和，a[i][j]表示当前格子的宝贝价值。

（2）我们可以编写递归型的动态规划函数来解决该问题。以下是一个示例的代码实现：

int max_value_recursive(vector<vector<int>>& a, int i, int j) {

if (i == m && j == n) {

return a[m][n];

} else if (i == m) {

return max_value_recursive(a, i, j+1) + a[i][j];

} else if (j == n) {

return max_value_recursive(a, i+1, j) + a[i][j];

} else {

return max(max_value_recursive(a, i+1, j), max_value_recursive(a, i, j+1)) + a[i][j];

}

}

a表示宝贝价值的矩阵，i和j表示当前格子的索引。当i == m && j == n时，即到达右下角格子，直接返回该格子的宝贝价值。否则，如果i==m，则只能向右走，调用递归函数计算右边格子的最大价值之和并

加上当前格子的宝贝价值。如果j为n，则只能向下走，调用递归函数计算下方格子的最大价值之和并加上当前格子的宝贝价值。否则，可以向下或向右走到达当前格子，取两者中的较大值作为当前格子的最大价值之和。

题目四

问题描述：

问题求解：

根据给定的二分查找递归算法，我们可以列出递归方程来分析其时间复杂性。

让我们定义递归函数的时间复杂性为T(n)，其中n表示输入数组的大小。

对于每次递归调用，算法将数组的一半大小进行处理。因此，递归方程可以表示为：

T(n) = T(n/2) + O(1)

其中T(n/2)表示递归调用的时间复杂性，O(1)表示每个递归步骤的常量时间复杂性。

根据递归方程，我们可以观察到每次递归调用都将问题规模缩小一半。这意味着递归树的高度为log₂ n。

递归树的每个层级的工作量都是O(1)，因为每次递归调用只需要常量时间。

因此，我们可以计算出递归函数的时间复杂性：

T(n) = O(1) + O(1) + ... + O(1) (总共log₂ n个O(1))

= O(log₂ n)

所以，该二分查找递归算法的时间复杂性为O(log₂ n)。

题目五

问题描述：

问题求解：

该贪心算法的基本思想是将作业按照它们的处理时间进行排序，然后将每个作业分配给当前空闲

时间最早的机器。

具体来说，算法的步骤如下：

1.初始化m台机器的空闲时间为0。

2.对作业列表按照处理时间进行递减排序。这样做的目的是让处理时间较长的作业优先分配给机

器，以便尽早释放机器的空闲时间。

3.依次遍历排序后的作业列表。

4.对于每个作业，找到当前空闲时间最早的机器，即空闲时间最小的机器。将该作业分配给这台

机器，并更新该机器的空闲时间。更新方法是将作业的处理时间加上该机器的当前空闲时间。

5.重复步骤4，直到所有作业都被分配给机器。

通过按处理时间排序并优先分配处理时间较长的作业，可以使得每台机器的空闲时间尽可能早地

释放出来，从而缩短整体作业完成时间。

题目六

问题描述：

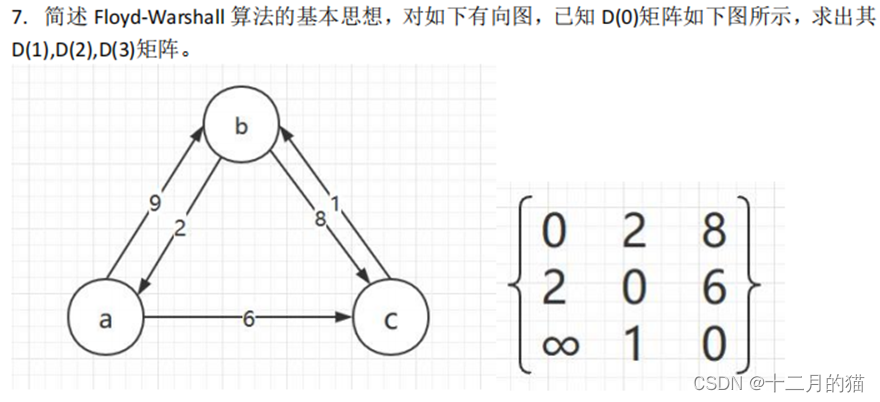
问题求解：

假设a、b、c分别记为1、2、3

D(0):

| 0 9 6 |

| 2 0 8 |

| ∞ 1 0 |

对所有 i 和 j，通过顶点 a 更新 D:

D(b,c)=min(D(b,c),D(b,a)+D(a,c))=min(8,2+6)=8 (无变化)

D(c,b)=min(D(c,b),D(c,a)+D(a,b))=min(1,∞+9)=1 (无变化)

D1：

| 0 9 6 |

| 2 0 8 |

| ∞ 1 0 |

D(2):

| 0 9 6 |

| 2 0 8 |

| 3 1 0 |

D(3):

| 0 7 6 |

| 2 0 8 |

| 3 1 0 |