微分先行PID控制的结构如图1所示,其特点是只对输出量y(k)进行微分,而对给定值y(k)不作微分。这样,在改变给定值时,输出不会改变,而被控量的变化通常是比较缓和的。这种输出量先行微分控制适用于给定值yd(k)频繁升降的场合,可以避免给定值升降时所引起的系统振荡,从而明显地改善了系统的动态特性。
令微分部分的传递函数为:
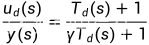


图1 微分先行ID控制结构图
仿真实例:
设被控对象为一延迟对象:
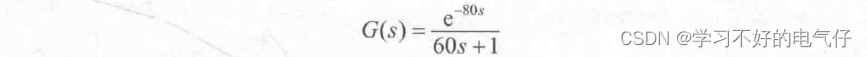
采样时间为20s,延迟时间为4个采样时间,即 80s。采用PID控制器进行阶跃响应。输入信号为带有高频干扰的方波信号: yd(t)= 1.0sgn(sin(0.0005*pi*t)+0.05sin(0.03*pi*t)。
取M=1,采有微分先行PID控制方法,其方波响应结果如图2所示。取M=2,采用普通PID方法,其方波响应控制结果如图3所示。由仿真结果可以看出,对于给定值yd(k)频繁升降的场合,引入微分先行后,可以避免给定值升降时所引起的系统振荡,明显地改善了系统的动态特性。

图2 微分先行PID控制方波响应(M=1)
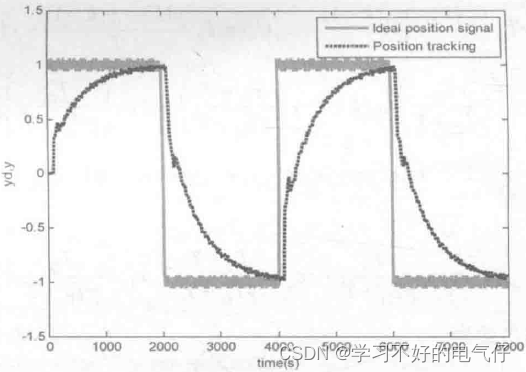
图3 普通PID控制方波响应(M=2)
仿真程序:
clear all;
close all:
ts=20;
sys=tf([1],[60,1],'inputdelay',80);
dsys=c2d(sys,ts, 'zoh');
[num,den]=tfdata(dsys,'v');
u_1=0;u_2=0;u_3=0;u_4=0;u_5-0;ud_1=0;
yL1=0;y_2=0;y_3=0;error_I=0;error_2=0;
ei=0;
for k=1: 1:400
time(k)=k*ts;
%Linear model
y(k)=-den(2)*y_1+num(2)*u_5;
kp=0.36;kd=14;ki=0.0021;
yd(k)=1.0*sign(sin(0.00025*2*pi*k*ts));
yd(k)=yd(k)+0.05*sin(0.03*pi*k*ts);
error(k)=yd(k)-y(k);
ei=eiterror(k)*ts;
gama=0.50;
Td=kd/kp;
Ti=0.5;
c1=gama*Td/(gama*Td+ts);
c2=(Td+ts)/(gama*Td+ts);
c3=Td/(gama*Td+ts);
M=2;
if M==1
ud(k)=cl*ud l+c2*y(k)-c3*y_l;
u(k)=kp*error(k)+ud(k)+ki*ei;
elseif M==2 %Simple PID Control
u(k)=kp*error(k)+kd*(error(k)-error_1Y/ts+ki*ei;end
if u(k)>=110
u(k)=110;
end
if u(k)<=-110
u(k)=-110;
end
%Update parameters
u_5=u_4;u_4=u_3;u_3=u_2;u_2=u_1;u_1=u(k);
y_3=y_2;y_2=y_1:y_1=y(k);
error_2=error_1;
error_I=error(k);
end
figure(1);
plot(time,yd,'r',time,y,'k:', linewidth',2);xlabel('time(s)');ylabel('yd.y');
legend(Ideal position signal' 'Position tracking');figure(2);
plot(time,u,'r','linewidth',2);xlabel( 'time(s)');ylabel('u');