质数（素数）的几种判断方法

news2025/4/27 1:23:07

判断一个数是否为质数/合数是在数据处理中经常遇到的问题，如何解决这个问题，作者总结了如下几种算法。

质数的定义：

一个数如果除了1 和 其本身外，不能被其它数整除，就称这个数为质数（或素数）。

合数的定义：

一个数除了1和其本身外，还可以被其它数整除，那么就称这个数为合数。

  • 第一种：枚举法

这个方法的思想就是利用质数的定义来进行枚举判定。例如，判断数字N是否为质数，那么就逐一判断2～N-1 范围内的每一个数，是否可以被N整除，只要在这个范围内存在任意一个可以被N整除的数，就称N 为非质数。

//代码段1

//10000内的所有质数的个数

#include <stdio.h>
#define MAX_N 10000


int is_prime(int n){
    for(int i = 2;i < n-1;i++){
        if(n % i == 0) return 0;
    }
    return 1;
}
int main(){
    int count = 0;
    for(int i = 2;i <= MAX_N;i++){
        if(is_prime(i)) ++count ;
    }
    printf("num is %d\n",count);
    return 0;
}

运行结果：

 

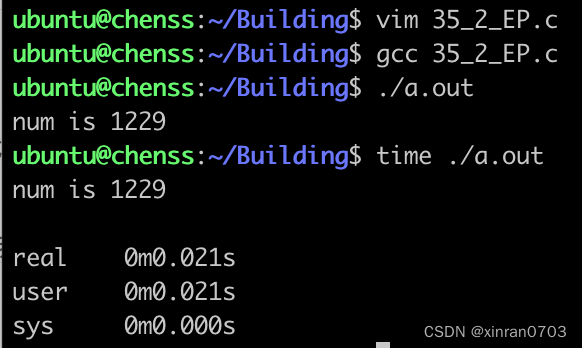
在10000以内，存在1229个质数，运行这段枚举代码用了0.21秒。 

枚举法分析：

优点：通过定义去判断，代码实现思路易于理解；

缺点：如果数据范围较大，即N值较大，在2～N-1 范围内逐一枚举，判断枚举值是否可以被N值整除，效率较低；

  • 第二种 优化枚举法

第一种方法的缺点显而易见，在进行枚举判断时的枚举范围是2～N-1， 缩小枚举范围就是优化方向。

我们知道，如果一个数N是合数，那么一定存在这样的关系：N = a*b （a和b 均不等于1 或者N本身） ，且因为存在 N = \sqrt{N} * \sqrt{N}；所以，a 一定大于或等于 \sqrt{N}， 而b一定小于或等于\sqrt{N}，不存在a和b同时大于或同时小于\sqrt{N}的情况。因此，枚举范围可以修改为2～\sqrt{N}， 因为，如果N是合数，那么在这个范围内必然存在一个它的因子。

//代码段2

//10000内所有质数的总个数

#include <stdio.h>
#include <math.h>

#define MAX_N 10000

int is_prime(int n){
    for(int i = 2，I = sqrt(n);i<= I;i++){
        if(n % i == 0) return 0;
    }
    return 1;
}

int main(){
    int count = 0;
    for(int i = 2;i <= MAX_N;i++){
        if(is_prime(i)) ++count;
    }
    printf("num is %d\n",count);
    return 0;
}

运行结果：

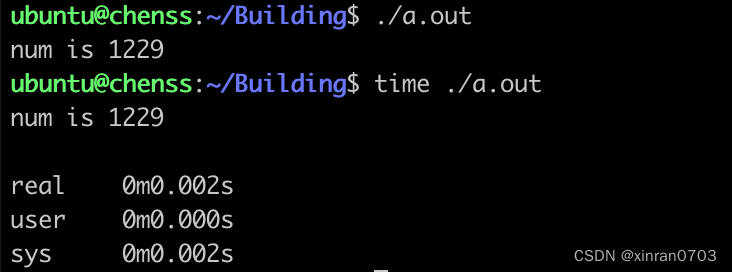
将枚举范围由2～N-1 缩小到2～\sqrt{N} 后，运行时间由0.21缩短到0.002秒。

优缺点分析：

优点：通过缩小枚举范围，运行时间得到了显著提成；

缺点：时间复杂度依然是0（n*n）

小技巧：

在下述代码段中，如果数据规模是100000， 那么采用优化前的“代码段A”，程序的运行时间为0.25秒，如果采用优化后的“代码段B”，程序的运行时间为0.11秒，这是因为函数sqrt在代码段A中被调用了sqrt(n)次，执行了sqrt(n)  次的函数入栈出栈操作，但是在代码段B，sqrt函数只执行了一次。

//代码段3

//优化前，代码段A：
int is_prime(int n){
    for(int i = 2; i<= sqrt(n);i++){
        if(n % i == 0) return 0;
    }
    return 1;
}

//优化后，代码段B：
int is_prime(int n){
    for(int i = 2，I = sqrt(n);i<= I;i++){
        if(n % i == 0) return 0;
    }
    return 1;
}
  • 第三种 素筛法

素筛法是通过逐步排除合数来识别素数的一种数学算法。

总体思想：

用素数去标记掉所有不是素数的数字，如果i是素数，那么所有i 的整数倍就不是素数。

代码实现思路：

1. 构建一个额外的数据存储空间  int prime[N]；

2. 用pirme[i] 来标记i是否为合数；

3. 第一次知道2 是素数，则将2的倍数都标记为1；

4. 向后找到第一个没有被标记的数字i；

5.将i的倍数全部标记为合数；

6. 重复4-5步，直到标记为你范围内的所有数字；

//代码段4

#include <stdio.h>

#define MAX_N 100
int prime[MAX_N+5] = {0};
void init_prime(){
    for(int i = 2;i <= MAX_N;i++){
        if(prime[i] == 0){
            for(int j = 2, I = MAX_N/i; j <= I; j++){ //如果运行的这个行，表示i为质数；
                prime[j*i] = 1; // 将i的整数倍的值，都标记
            } 
        }
    }
    return;
}
int main(){
    init_priem(); 
    int cnt = 0; //用于计数，统计0～MAX_N 范围内有有多少个质数；
    for(int i = 2;i <= MAX_N;i++){
        if(prime[i] == 0) ++cnt;
    }
    printf("num is %d\n",cnt);
    return 0;
}

素筛法优化 之一

在代码段4 的init_prime() 函数中存在多层缩紧，为了提高代码的可读性，采用名为“对偶逻辑”

的编程技巧，所谓“对偶逻辑”就是对立的逻辑。

//代码段5
void init_prime(){
    for(int i = 2;i <= MAX_N;i++){
        if(prime[i]) continue;
        for(int j = 2, I = MAX_N/i; j <= I; j++){ 
            prime[i*j] = 1;
        }
    }
    return;
}

素筛法优化 之二

当前的init_prime() 函数已经做到了对数据范围内的所有数值进行了是否为质数的判断，如果i为质数，则prime[i] 等于0， 如果i为合数，则pirme[i] 为1.

是否可以将筛查出的质数保存到一个数据结构中？当然可以。

思路1: 申请一个数组， int primeValue[MAX_N+5] = {0}; 则 primeValue[0] = 2; primeValue[1] = 3;primeValue[2] = 5; ... 但是这么做增加了内存空间的开销；

思路2: 不额外的申请内存 ，只使用  int prime[MAX_N+5]

// 代码段6
#include <stdio.h>

#define MAX_N 100000

int prime[MAX_N+5] = {0};

void init_Prime(){
    for(int i = 2;i <= MAX_N;i++){
        if(prime[i]) continue;
        prime[++Prime[0]] = i; // 如果执行到这一行，说明i为质数，从prime[1] 开始依次存放找到的质数；++Prime[0] 说明每找到一个质数，prime[0]的值加1，当函数执行完毕，prime[0]代表质数的总个数
        for(int j = 2,I =MAX_N/i; j<=I; j++){
            prime[i*j] = 1;
        }
    }
}

int main(){
    init_prime();
    for(int i = 1;i <= prime[0];i++){
        printf("%d ", prime[i]);
        if(i % 10 == 0) printf("\n"); // 一行打印10个数据；
    }
    
    return 0;
}

素筛法应用举例

例题1: 求出一个范围内（假设20）所有数字的最小素因子

解析：一个质数 N , 它只有1和它本身两个因子，因此它只存在一个因式 N = 1*N， 又因为1为非质数，所以质数N的最小素因子就是其本身。

编程思路：利用素筛法

#include <stdio.h>
#define MAX_N 20

int prime[MAX_N+5] = {0}; //存放对应数据的素因子；

void init_prime(){
    for(int i = 2;i <= MAX_N;i++){
        if(prime[i]) continue;
        prime[i] = i; //i为质数，最小素因子即为i本身
        for(int j = 2, I <= MAX_N/i; j<=I; j++){
            if(prime[i*j]) continue; //如果已经被标记过，说明存储了最小素因子；
            prime[i*j] = i;
        }
    }
    return;
}

int main(){
    init_prime();
    for(int i = 2;i<= MAX_N;i++){
        printf("min[%d] = %d\n",i, prime[i]);
    }
    return 0;
}

运行结果：

例题1: 求出一个范围内（假设20）所有数字的最大素因子 

解析：例如 数据 20，它的因式可有表示为：2*10； 5*4； 所以它的最大素因子就是5；

#include <stdio.h>
  
#define MAX_N 20
int prime[MAX_N] = {0};
 void init_prime(){
     for(int i  = 2; i <= MAX_N;i++){
          if(prime[i]) continue;
          prime[i] = i;
          for(int j = 2, I=MAX_N/i; j<=I; j++){
              prime[i*j] = i;
          }
    }
  }
  int main(){
      init_prime();
      for(int i = 2;i <= MAX_N;i++){
         printf("MAX(%d) = %d\n",i, prime[i]);
      }
     return 0;
  }

运行结果：

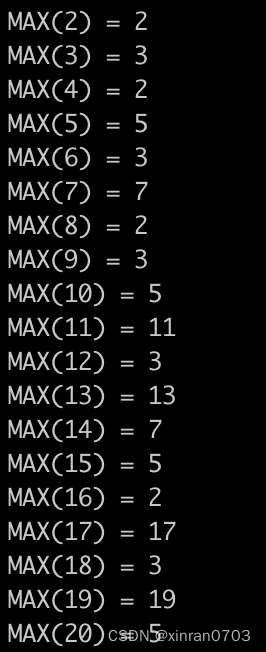
  • 第四种 线性筛算法

在上述素筛法的实现过程中，存在数据被多次标记的情况。

例如：合数6被标记了几次？当前质数为2时，标记2的倍数，6被标记了一次，当执行到质数3时，6作为3的倍数，又被标记了一次，所以，6被标记了2次。

通过分析，一个存在m个质数因子的合数，将被标记m次 （参考代码6的init_prime() 函数）。

例如：30 被标记了几次？30存在的质数因子为：2，3，5，所以，它将被标记3次。

为了解决合数被重复标记的问题，可以采用线性筛算法。

算法思想：

1. 标记一个范围内的数字是否为合数，没有被标记的则为素数。

2. 算法的空间复杂度为O(N), 时间复杂度为O(N)

3. 一个合数N的n个因子中，最小的那个素数因子p，被称为最小素因子，线性筛算法的思想就是用满足等式N=m*p的中的m去标记N。同样以30为例，它的所有因式如下：

因式1:   1*30

因式2:   2*15

因式3:   3*10

因式4:   5*6

因式5:   6*5

因式6:  10*3

因式7:  15*2

因式8:  30*1

由于因式1和因式8是由 数字1和它本身构成，不予考虑。如果使用素筛法时，参见代码段6的init_prime() 函数，当i = 2，3，5时，30都会被标记一次，但是线筛法的思想是，找到最小素因子2所对应的因子15，用15*2 标记出30，因为15是30的最大因子，是30的对后一个因式，是i值循环加加的过程中，最后一次得到30的机会，用来标记30，30的有且一次的标记机会。

所以，N和m有如下性质：

1. N中最小的素数为p

2. N可以表示成P*m

3. p一定小于等于m中最小的素因子（即：m不是p的整数倍，如果m是p的整数倍，那么p就不是N的最小素因子）

4. 利用M*{p}' （所有不大于m中最小素数的集合）标记N1，N2，N2....

代码实现

#include <stdio.h>

#define MAX_N 100

int prime[MAX_N+5] = {0};

void init_prime(){
    for(int i = 2;i <= MAX_N;i++){  // i值为m
        if(!prime[i]) prime[++prime[0]] = i;
        for(int j = 1;j <= prime[0]; j++){
            if(prime[j] *i > MAX_N) break;
            prime[prime[j]*i] = 1;  // 通过m*p 找到对应的N 
            if(i % prime[j] == 0) break;
        }
    }
    return 0;
}

int main(){
    init_prime();
    for(int i = 1;i <= prime[0]; i++){
        printf("%d\n",prime[i]);
    }
    return 0;
}

线性筛算法应用：

题目： 所有小于10的质数的和是2+3+5+7 = 17。求所有小于两百万的质数的和。

解析：

第一步：求出200万内的质数

第二步：求出质数和

//利用线性筛算法求200万内的质数和

#include <stdio.h>

#define MAX_N 2000000

int prime[MAX_N+5] = {0}

void init_prime(){
    for(int i = 0;i <= MAX_N; i++){
        if(!prime[i]) prime[++prime[0]] = i;
        for(int j = 1; j < prime[0];j++){
            if(prime[j]*i > MAX_N) break;
            prime[prime[j]*i] = 1;
            if(i % prime[j] == 0) break;
        }
    }
    return;
}

init main(){
    long long sum = 0;
    for(int i = 1; i <= prime[0]; i++){
        sum += prime[i];
    }
    printf("sum = %lld\n",sum);
    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1814631.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【计算机体系结构复习】

【计算机体系结构复习】

一.选择题&#xff08;2 X 15) 第五章第六章没有 第一章 第二章 第三章 第四章 第七章 第八章 二.主观题 第一章 1.7 1.11 怎么计算程序执行时间CPI、MIPS CPI变化&#xff0c;系统性能怎么变&#xff08;上课例子&#xff09; p9 例1.3 第二章 哈夫曼…
阅读更多...
CVE-2012-2122-mysql未授权访问漏洞复现-vulhub

CVE-2012-2122-mysql未授权访问漏洞复现-vulhub

1.原理 参考&#xff1a;CVE-2012-2122 Mysql身份认证漏洞及利用-CSDN博客 简单来说&#xff0c;除了配置上的问题以外&#xff0c;是密码的验证出现了漏洞&#xff0c;导致尝试次数多了之后直接可以登入 使用&#xff1a;kalivulhub 2.复现 开一下镜像&#xff0c;用的是v…
阅读更多...
Michael.W基于Foundry精读Openzeppelin第57期——ReentrancyGuard.sol

Michael.W基于Foundry精读Openzeppelin第57期——ReentrancyGuard.sol

Michael.W基于Foundry精读Openzeppelin第57期——ReentrancyGuard.sol 0. 版本0.1 ReentrancyGuard.sol 1. 目标合约2. 代码精读2.1 constructor()2.2 modifier nonReentrant() 0. 版本 [openzeppelin]&#xff1a;v4.8.3&#xff0c;[forge-std]&#xff1a;v1.5.6 0.1 Reen…
阅读更多...
docker-compose Install wiki

docker-compose Install wiki

wiki 前言 最强大和可扩展的开源Wiki软件，使用Wiki.js漂亮而直观的界面，让编写文档成为一种乐趣 前提要求 安装 docker docker-compose 参考创建一键安装wiki wiki 安装目录/wikiwiki端口83admin 端口 84postgres 端口5432postgres 库 wikipostgres 用户 wikijspostgres 密…
阅读更多...
【启明智显方案分享】ESP32-S3与GPT AI融合的智能问答嵌入式设备应用解决方案

【启明智显方案分享】ESP32-S3与GPT AI融合的智能问答嵌入式设备应用解决方案

一、引言 随着物联网&#xff08;IoT&#xff09;和人工智能&#xff08;AI&#xff09;技术的飞速发展&#xff0c;嵌入式设备正逐渐变得智能化。本解决方案是启明智显通过结合ESP32-S3的低功耗、高性能特性和GPT&#xff08;Generative Pre-trained Transformer&#xff09;…
阅读更多...
简单了解java中线程的使用

简单了解java中线程的使用

线程 1、线程的相关概念 1.1、并行和并发 并行&#xff1a;在同一时刻&#xff0c;有多个任务在多个CPU上同时执行 并发&#xff1a;在同一时刻&#xff0c;有多个任务在单个CPU上交替执行 1.2、进程和线程 进程&#xff1a;就是在多任务管理系统中&#xff0c;每个独立执…
阅读更多...
【MySQL】表的基本增删查改（结合案例）

【MySQL】表的基本增删查改（结合案例）

文章目录 1.前言2.插入数据&#xff08;Create&#xff09;2.1案例2.2单行数据全列插入2.3多行数据指定列插入2.4插入否则更新2.5替换 3. 读取数据(Retireve)3.1案例3.2全列查询3.3指定列查询3.4查询字段为表达式3.5为查询结果起别名3.6去重3.7where条件3.7.1案例 3.8排序3.9筛…
阅读更多...
Post Microsoft Build and AI Day 北京开发者日

Post Microsoft Build and AI Day 北京开发者日

Microsoft Build 开发者大会 Microsoft Build 开发者大会是微软每年一次的开发者技术盛会&#xff0c;旨在向全球开发者展示微软最新的技术、产品和服务。 刚刚过去的 2024 Microsoft Build 开发者大会围绕 Copilot、生成式 AI、应用程序安全、云平台、低代码等多个技术方向&a…
阅读更多...
运维系列.在Docker中使用Grafana

运维系列.在Docker中使用Grafana

运维专题 在Docker中使用Grafana - 文章信息 - Author: 李俊才 (jcLee95) Visit me at CSDN: https://jclee95.blog.csdn.netMy WebSite&#xff1a;http://thispage.tech/Email: 291148484163.com. Shenzhen ChinaAddress of this article:https://blog.csdn.net/qq_2855026…
阅读更多...
Java对象的序列化与反序列化

Java对象的序列化与反序列化

序列化和反序列化是什么 当两个进程远程通信时&#xff0c;彼此可以发送各种类型的数据。无论是何种类型的数据&#xff0c;都会以二进制序列的形式在网络上传送。比如&#xff1a;我们可以通过http协议发生字符串信息&#xff1b;我们也可以在网络上直接发生Java对象。发送方…
阅读更多...
【linux】信号（三）

【linux】信号（三）

本章节将会围绕信号处理进行展开讲解 目录 回顾一下&#xff1a;历史问题&#xff1a;内核态 VS 用户态地址空间&#xff1a;键盘的输出如何被检测到&#xff1a;OS如何正常运行&#xff1a;如何执行系统调用&#xff1a; 信号的处理&#xff1a;sigaction&#xff1a;信号的…
阅读更多...
QML学习十九：ttf字体库使用

QML学习十九：ttf字体库使用

一、前言 在使用QML时&#xff0c;常常自定义按钮&#xff0c;按钮上有显示个图标&#xff0c;其实&#xff0c;那不是图标&#xff0c;是文本&#xff0c;如何显示&#xff1f; 本篇记录&#xff0c;如何导入阿里巴巴字体库&#xff0c;并调用显示。 二、阿里巴巴字体库下载…
阅读更多...
分布式系统设计指南

分布式系统设计指南

目录 一、分布式简介 二、分布式系统核心概念 2.1 CAP 理论 2.2 BASE 原理 三、分布式系统设计 3.1 微服务拆分 3.2 通信模型 3.3 负载均衡 3.4 数据一致性 3.5 容错限流 3.6 扩展性 3.7 监控预警 3.8 自动化运维 一、分布式简介 分布式系统是由单体应用发展而来的&#xff…
阅读更多...
统计绘图 | 既能统计分析又能可视化绘制的技能

统计绘图 | 既能统计分析又能可视化绘制的技能

在典型的探索性数据分析工作流程中&#xff0c;数据可视化和统计建模是两个不同的阶段&#xff0c;而我们也希望能够在最终的可视化结果中将相关统计指标呈现出来&#xff0c;如何让将两种有效结合&#xff0c;使得数据探索更加简单快捷呢&#xff1f;今天这篇推文就告诉你如何…
阅读更多...
使用 Scapy 库编写 TCP 窗口大小探测攻击脚本

使用 Scapy 库编写 TCP 窗口大小探测攻击脚本

一、介绍 1.1 概述 TCP窗口大小探测攻击是一种信息收集攻击&#xff0c;攻击者通过向目标服务器发送特制的TCP数据包&#xff0c;探测目标服务器的TCP接收窗口大小&#xff08;TCP Window Size&#xff09;。了解目标服务器的TCP接收窗口大小&#xff0c;可以帮助攻击者优化后…
阅读更多...
Spring Web MVC之过滤器Filter和拦截器HandlerInterceptor的区别和用法

Spring Web MVC之过滤器Filter和拦截器HandlerInterceptor的区别和用法

作用时机不一样 Spring 框架有一个很重要的类DispatcherServlet。这个类继承了HttpServlet&#xff0c;HttpServlet实现了Servlet接口。相当于图片中的Servlet。所有和Spring框架相关配置&#xff0c;例如注解、xml配置、其他数据库连接配置、bean配置、拦截器配置等其他配置&…
阅读更多...
深度学习研究生的职业前景：未来趋势与机遇

深度学习研究生的职业前景：未来趋势与机遇

deep learning 深度学习研究生的职业前景&#xff1a;未来趋势与机遇一、深度学习的应用领域1. 计算机视觉2. 自然语言处理&#xff08;NLP&#xff09;3. 数据分析4. 游戏开发5. 健康医疗 二、职业机遇与挑战1. 工作机会2. 竞争与挑战3. 薪资前景 三、职业发展策略对于深度学习…
阅读更多...
国外创意二维码应用：飞利浦旧物翻新活动，传播可持续性消费的重要性！

国外创意二维码应用：飞利浦旧物翻新活动，传播可持续性消费的重要性！

你知道去年有超过1000万件礼物被扔进了垃圾场吗? 这些被丢弃的物品中有许多仍在使用&#xff0c;飞利浦希望改变这种浪费现象。 去年的地球日&#xff0c;飞利浦策划了一场名为“Better than New” 的二维码营销活动。他们发布了一个视频&#xff0c;通过这个短视频将所有最终…
阅读更多...
钉钉魔点指纹考勤机多少钱一台，指纹门禁考勤一体机价格

钉钉魔点指纹考勤机多少钱一台，指纹门禁考勤一体机价格

钉钉魔点指纹考勤机一台多少钱呢&#xff0c;指纹门禁考勤一体机的价格又是多少 钉钉魔点 X2 智能指纹考勤门禁一体机的参考价格是 359 元。 其具体参数情况如下&#xff1a; 产品类型&#xff1a;属于指纹考勤门禁一体机&#xff1b; 验证方式&#xff1a;为电容指纹&…
阅读更多...
4、优化阶段

4、优化阶段

优化概述 编译程序总框架&#xff1a; 优化:对程序进行各种等价变换&#xff0c;使得从变换后的程序出发&#xff0c;能生成更有效的目标代码。 等价:不改变程序的运行结果。 有效:目标代码运行时间短&#xff0c;占用存储空间小。 >目的 产生更高效的代码 >遵循的原则 …
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023