- 👋 Hi, I’m @Beast Cheng
- 👀 I’m interested in photography, hiking, landscape…
- 🌱 I’m currently learning python, javascript, kotlin…
- 📫 How to reach me --> 458290771@qq.com
喜欢《数据结构》部分笔记的小伙伴可以订阅专栏,今后还会不断更新。🧑💻
此外,《程序员必备技能》专栏日后会逐步更新,感兴趣的小伙伴可以点一下订阅、收藏、关注!🚀
谢谢大家!🙏
数组的存储结构
一维数组
ElemType a[10]; // ElemType型一维数组
起始地址:LOC
各数组元素大小相同且物理上连续存放
数组元素a[i]的存放地址 =
L
O
C
+
i
∗
s
i
z
e
o
f
(
E
l
e
m
T
y
p
e
)
LOC+i*sizeof(ElemType)
LOC+i∗sizeof(ElemType)
(
0
<
=
i
<
10
)
(0 <= i < 10)
(0<=i<10)
注:除非题目特别说明,否则数组下标默认从0开始
二维数组
ElemType b[2][4]; // 2行4列的二维数组
起始地址:LOC
M行N列的二维数组b[M][N]中
- 若按行优先存储,则
b[i][j]的存储地址 = L O C + ( i ∗ N + j ) ∗ s i z e o f ( E l e m T y p e ) LOC + (i*N+j)*sizeof(ElemType) LOC+(i∗N+j)∗sizeof(ElemType) - 若按列优先存储,则
b[i][j]的存储地址 = L O C + ( i + j ∗ M ) ∗ s i z e o f ( E l e m T y p e ) LOC+(i+j*M)*sizeof(ElemType) LOC+(i+j∗M)∗sizeof(ElemType)
特殊矩阵
普通矩阵
∣
a
1
,
1
a
1
,
2
a
1
,
3
.
.
.
.
.
.
a
1
,
n
−
1
a
1
,
n
a
2
,
1
a
2
,
2
a
2
,
3
.
.
.
.
.
.
a
2
,
n
−
1
a
2
,
n
a
3
,
1
a
3
,
2
a
3
,
3
.
.
.
.
.
.
a
3
,
n
−
1
a
3
,
n
⋮
⋮
⋮
⋮
⋮
a
n
,
1
a
n
,
2
a
n
,
3
.
.
.
.
.
.
a
n
,
n
−
1
a
n
,
n
∣
\begin{vmatrix} a_{1,1}&a_{1,2}&a_{1,3}&......&a_{1,n-1}&a_{1,n}\\ a_{2,1}&a_{2,2}&a_{2,3}&......&a_{2,n-1}&a_{2,n}\\ a_{3,1}&a_{3,2}&a_{3,3}&......&a_{3,n-1}&a_{3,n}\\ \vdots&\vdots&\vdots&\,&\vdots&\vdots\\ a_{n,1}&a_{n,2}&a_{n,3}&......&a_{n,n-1}&a_{n,n}\\ \end{vmatrix}
a1,1a2,1a3,1⋮an,1a1,2a2,2a3,2⋮an,2a1,3a2,3a3,3⋮an,3........................a1,n−1a2,n−1a3,n−1⋮an,n−1a1,na2,na3,n⋮an,n
可用二位数组存储
注意:描述矩阵元素时,行、列号通常从 1 开始;而描述数组时通常下标从 0 开始(具体看题目给的条件,注意审题)
对称矩阵的压缩存储
若 n 阶方阵中任意一个元素
a
i
,
j
a_{i,j}
ai,j 都有
a
i
,
j
=
a
j
,
i
a_{i,j}=a_{j,i}
ai,j=aj,i ,则称该矩阵为对称矩阵
∣
a
1
,
1
a
1
,
2
a
1
,
3
.
.
.
.
.
.
a
1
,
n
−
1
a
1
,
n
a
2
,
1
a
2
,
2
a
2
,
3
.
.
.
.
.
.
a
2
,
n
−
1
a
2
,
n
a
3
,
1
a
3
,
2
a
3
,
3
.
.
.
.
.
.
a
3
,
n
−
1
a
3
,
n
⋮
⋮
⋮
⋱
⋮
⋮
a
n
−
1
,
1
a
n
−
1
,
2
a
n
−
1
,
3
.
.
.
.
.
.
a
n
−
1
,
n
−
1
a
n
−
1
,
n
a
n
,
1
a
n
,
2
a
n
,
3
.
.
.
.
.
.
a
n
,
n
−
1
a
n
,
n
∣
\begin{vmatrix} a_{1,1}&a_{1,2}&a_{1,3}&......&a_{1,n-1}&a_{1,n}\\ a_{2,1}&a_{2,2}&a_{2,3}&......&a_{2,n-1}&a_{2,n}\\ a_{3,1}&a_{3,2}&a_{3,3}&......&a_{3,n-1}&a_{3,n}\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\ a_{n-1,1}&a_{n-1,2}&a_{n-1,3}&......&a_{n-1,n-1}&a_{n-1,n}\\ a_{n,1}&a_{n,2}&a_{n,3}&......&a_{n,n-1}&a_{n,n}\\ \end{vmatrix}
a1,1a2,1a3,1⋮an−1,1an,1a1,2a2,2a3,2⋮an−1,2an,2a1,3a2,3a3,3⋮an−1,3an,3..................⋱............a1,n−1a2,n−1a3,n−1⋮an−1,n−1an,n−1a1,na2,na3,n⋮an−1,nan,n
普通存储:
n
∗
n
n*n
n∗n 二维数组
压缩存储:只存储主对角线+下三角区
- 策略:只存储主对角线+下三角区
按行优先原则将各元素存入一维数组中
思考:
- 数组大小应该为多少?
- n ( n + 1 ) 2 \frac{n(n+1)}{2} 2n(n+1)
- 站在程序员的角度,对称矩阵压缩存储后怎样才能方便使用?
- 可以实现一个“映射”函数,矩阵下标->一维数组下标
那么如何才能把矩阵的下标映射为一维数组的下标呢?
- 关键:按照行优先的原则且
(
i
≥
j
)
(i\geq j)
(i≥j) ,
a
i
,
j
a_{i,j}
ai,j 是数组
B
[
k
]
B[k]
B[k] 中的第几个元素?
- 根据下标 i ,前面有 i ( i − 1 ) 2 + j \frac{i(i-1)}{2}+j 2i(i−1)+j 个元素
- 所以 k = i ( i − 1 ) 2 + j − 1 k=\frac{i(i-1)}{2}+j-1 k=2i(i−1)+j−1 (如果有些数组下标从 1 开始,那么就不需要 -1 了
- 那么如果是
i
<
j
i<j
i<j 呢?
- 根据对称矩阵的性质,我们可以转变为访问 a j , i a_{j,i} aj,i
- 那么 k = j ( j − 1 ) 2 + i − 1 k=\frac{j(j-1)}{2}+i-1 k=2j(j−1)+i−1
三角矩阵
下三角矩阵:除了主对角线和下三角区,其余的元素都相同
上三角矩阵:除了主对角线和上三角区,其余的元素都相同
压缩存储策略:按行优先原则将橙色区元素存入一维数组中。并在最后一个位置存储常量 c
- 如果是下三角矩阵:
- 三角矩阵的下标映射为一维数组的下标和对称矩阵的一样:
k = { i ( i − 1 ) 2 + j − 1 , i ≥ j (下三角区和主对角线元素) j ( j − 1 ) 2 + i − 1 , i < j (上三角区元素) k=\begin{cases}\frac{i(i-1)}{2}+j-1,\,\,\,\,i\geq j\,\,(下三角区和主对角线元素)\\ \frac{j(j-1)}{2}+i-1,\,\,\,i<j\,\,\,(上三角区元素)\end{cases} k={2i(i−1)+j−1,i≥j(下三角区和主对角线元素)2j(j−1)+i−1,i<j(上三角区元素)
- 三角矩阵的下标映射为一维数组的下标和对称矩阵的一样:
- 如果是上三角矩阵:
k = { ( i − 1 ) ( 2 n − i + 2 ) 2 + ( j − i ) , i ≤ j (上三角区和主对角线元素) n ( n + 1 ) 2 , i > j (下三角区元素) k = \begin{cases}\frac{(i-1)(2n-i+2)}{2}+(j-i),\,\,\,\,i\leq j(上三角区和主对角线元素)\\ \frac{n(n+1)}{2},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,i>j(下三角区元素)\end{cases} k={2(i−1)(2n−i+2)+(j−i),i≤j(上三角区和主对角线元素)2n(n+1),i>j(下三角区元素)
三对角矩阵
三对角矩阵,又称带状矩阵:
当
∣
i
−
j
∣
>
1
|i-j|>1
∣i−j∣>1 时,有
a
i
,
j
=
0
(
1
≤
i
,
j
≤
n
)
a_{i,j}=0\,\,(1\leq i,j \leq n)
ai,j=0(1≤i,j≤n)
也就是说,主对角线上的元素都是非零元素,并且任意一个主对角线上的元素四周的元素都是非零元素,再往外的元素都是零元素
按照行优先(或列优先)原则,只存储带状部分
不难发现,前
i
−
1
i-1
i−1 行共有
3
(
i
−
1
)
−
1
3(i-1)-1
3(i−1)−1 个元素,
a
i
,
j
a_{i,j}
ai,j 应该是第 i 行的第
j
−
i
+
2
j-i+2
j−i+2 个元素,所以
a
i
,
j
a_{i,j}
ai,j 是第
2
i
+
j
−
2
2i+j-2
2i+j−2 个元素 -->
k
=
2
i
+
j
−
3
k=2i+j-3
k=2i+j−3
反之,如果已经知道数组下标 k ,如何得到 i,j?
前
i
−
1
i-1
i−1 共
3
(
i
−
1
)
−
1
3(i-1)-1
3(i−1)−1 个元素
前
i
i
i 行共
3
i
−
1
3i-1
3i−1 个元素
显然,
3
(
i
−
1
)
−
1
<
k
+
1
≤
3
i
−
1
3(i-1)-1<k+1\leq 3i-1
3(i−1)−1<k+1≤3i−1
当
i
=
(
k
+
2
)
3
i=\frac{(k+2)}{3}
i=3(k+2) ,向上取整,刚好可以满足上面那个表达式
稀疏矩阵
稀疏矩阵:非零元素远远少于矩阵元素的个数
压缩存储策略:
- 顺序存储——三元组(行,列,值)
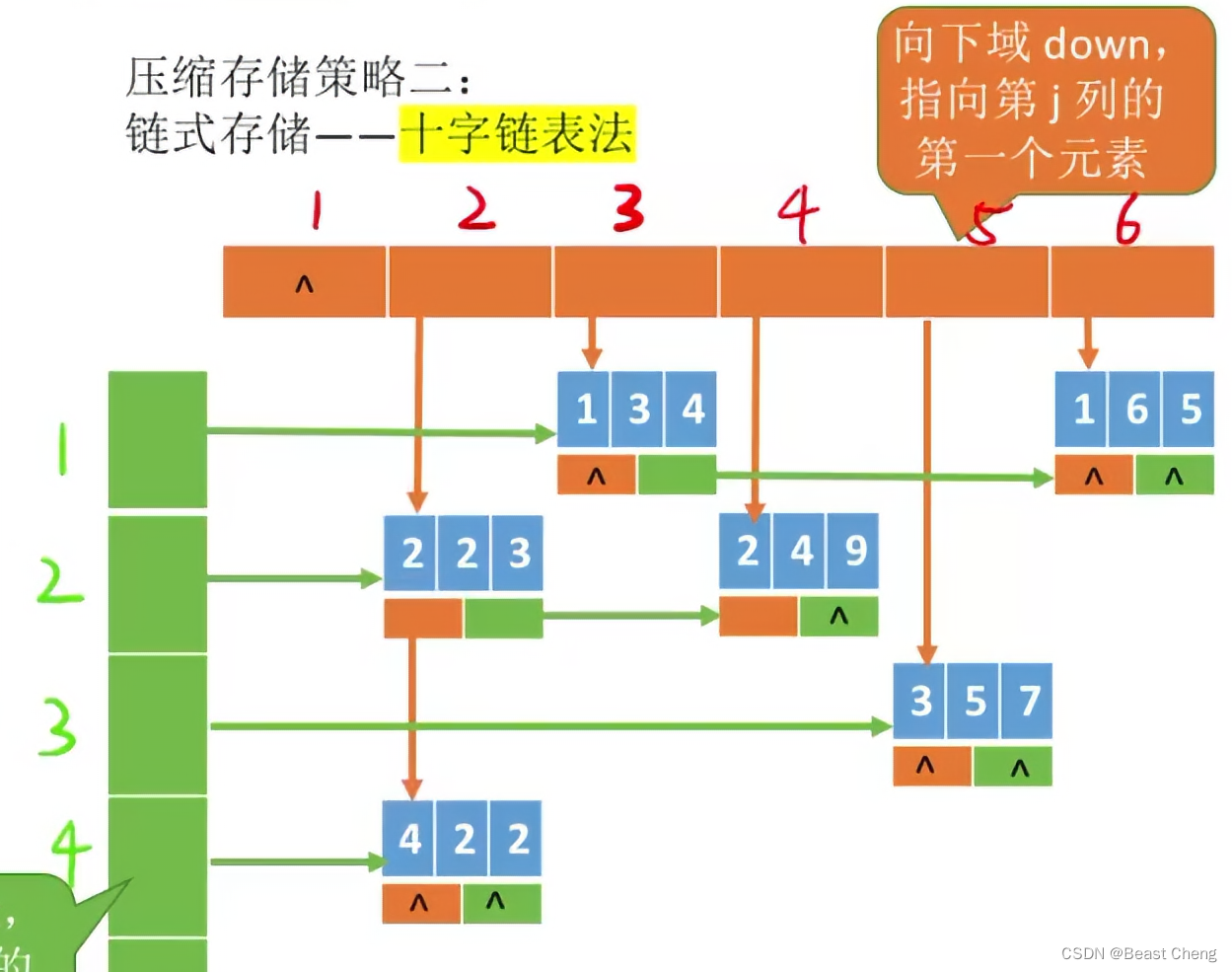
- 链式存储——十字链表法


![[工具探索]英寸vs毫米下常见尺寸排版](https://img-blog.csdnimg.cn/direct/ceea9c79d5c34964a96d2b59e381b237.jpeg#pic_center)