EGST:Explicit Geometric Structure Transformer论文解读

一、导言

二、相关工作

1、3D局部描述子

2、点云配准方法

三、EGST模型

1、结构化特征

2、特征提取

3、点云匹配

4、变换估计

5、损失函数

四、实验

1、数据集

2、评估指标

3、细节

4、对比实验

一、导言

该论文提出一种基于增强几何结构特征的点云配准方法EGST（Explicit Geometric Structure Transformer)用于编码显式几何结构。

（1）EGST构建了三种几何描述子来描述点云内部和外部结构，三种几何描述子：表面法线、差分向量、差分向量之间的夹角。

（2）Encoder部分使用structure attention来建立两对应点云间的结构一致性

（3）Decoder部分使用可学习的RPM来提取对应关系，并且在对抗离群点和噪声中保持鲁棒性，用几何结构特征的距离进行初始化，而非空间距离。

注意：本文没有使用显式Embedding，以及额外的特征注意力模块，如交叉注意力机制。

二、相关工作

1、3D局部描述子

LRF

LRF（Localized Receptive Field）局部特征子一般表示三维物体表面的局部区域，如局部的几何形状、法向量信息等，可以用来检测具体的物体部分或是整体形状，进而用于物体的识别和分割。一般的用到LRF的算法有：SHOT、RoPS、USC等。

（1）SHOT

SHOT算法中，根据特征点球邻域内建立局部参考坐标系LRF，对特征点在径向、经度、纬度三个方向进行区域划分，之后对每个区域的法向量夹角余弦值分布情况进行直方图统计（Bilinear interpolation）

（2）RoPS

RoPS算法中，对于给定的感兴趣点局部进行区域裁剪，并在裁剪区域建立LRF，然后旋转裁剪区域与三个轴Ox,Oy,Oz对齐，并将裁剪区域投影到yz，xz，xy平面，为每个投影区域建立分布矩阵。将每个投影区域离散成L*L个图像，提取更丰富的点云特征，最终目的是对于这些离散的图像区域，来统计其覆盖区域内的点云数据特征，并综合成一个特征描述向量，提高点云数据的表达描述能力。

PPF

PPF（Point Pair Feature）旋转不变点对特征，在匹配点云时具有旋转不变性，并考虑点对之间的对称性，以实现在旋转角度下的匹配关系。PPF算法中，首先选择一个参考点，并选取一个候选点，计算参考点与候选点间的特征，形成点对特征描述。

其他结构

（1）3DMatch使用截断距离函数，直接从两个点云间提取局部特征，这积累了巨大的参数量。

（2）PPFNet提出增强的PPF，引入严格的旋转不变性，但过分依赖数据，会对噪声和离群点异常敏感。

（3）GeoTransformer提出构建显式的内部几何关系，对其进行编码，由于点云的稀疏性（点与点间没什么太大的关系），引入了大量的位置编码，而这些位置编码是没意义的，缺少了点云的外部表示。

2、点云配准方法

ICP算法

ICP算法用于两个或多个点云数据集对齐，在ICP算法中，通过迭代计算最小化两个点云间的距离，来优化一个点云到另一个点云间的转换矩阵（R,T）。SVD一般用于计算最佳的变换矩阵，将点云的几何关系转化为代数问题，来优化点云的配准过程，减小对应点间误差（类似线性齐次方程组的最小二乘解）。

基于学习的方法

基于学习的方法通常分为无对应的方法和基于对应的方法。

无对应的方法先提取输入点云的全局特征向量然后将变换参数与全局特征向量进行回归，如PointNetLk方法，在小型数据集表现很好，但在大型数据集和复杂场景中表现较差。

基于对应的方法，在遵循ICP的思想下，建立对应的软分配（Soft assignment），用于处理对应点间的不确定性和模糊性。在传统的点对点对应方法，称为硬分配，而由于实际场景中存在噪声、遮挡，在点云配准中会出现一对多、多对一的映射关系。而使用软分配可以通过引入权重和概率，获得每个点对应的概率分布，以描述点云的模糊对应关系增强鲁棒性。如GeoTransformer。

三、EGST模型

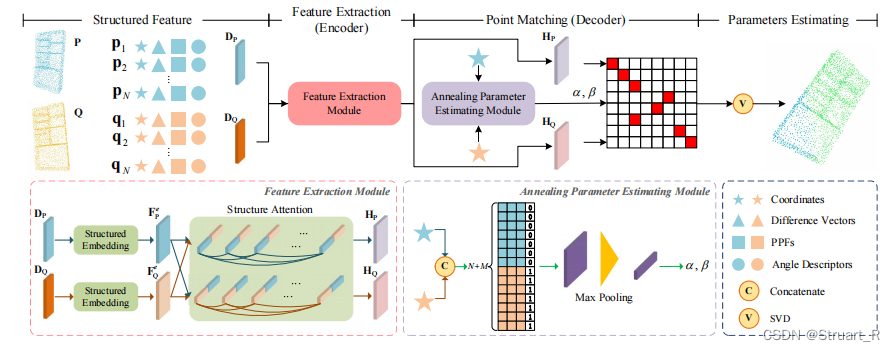
EGST模型由四个部分构成：结构化特征、特征提取（Encoder）、点云匹配（Decoder）、参数估计。

1、结构化特征

在原始坐标的基础上建立了三个几何特征子，分别为：差分向量、角度、表面法线。

对于这一部分的字母注释：

P：模板点云

Q：源点云（对源点云变换R，T得到模板点云）

$p_r$ :中心点，用于收集 $p_r$ 周围球形区域的点云集 $\left \{ p_1,p_2,...,p_f \right \}$

$p_{f}$ :点云集中的一个点

$p_{dis}(p_r,f)$ ：差分向量， $p_{dis}(p_r,f)=p_r-p_f \in K$ （三维向量）

$p_{ppf}(p_r,f)$ ：点对特征（四维向量） $p_{ppf}(p_r,f)=cat(\angle (n_r,p_{dis}(p_r,f)), \angle(n_f,p_{dis}(p_r,f)),\angle(n_r,n_f),||p_{dis}(p_r,f)||_2)$

其中 $\angle(\cdot _1,\cdot_2)=atan2(||\cdot_1 \times \cdot_2||,(\cdot_1) \cdot (\cdot_2))$ ，计算了向量夹角的弧度值。

$p_{ang}(p_r,f)$ ：角度， $p_{arg}(p_r,f)=\angle(max R,p_{dis}(p_r,f))$ （标量）

其中 $R=\left \{ d_{rv}=p_v-p_r|p_v \in P,v=1,2,...,N \right \}$ , $d_{rv}$ 为全局差分信息（参考向量），P对应全局若干中心点。

$D_P$ ：模板点云的组合向量，十一维向量，由上述若干特征组合而成。 $D_P=cat(p_{xyz}(p_r),p_{dis}(p_r,f),p_{ppf}(p_r,f),p_{ang}(p_r,f))$ ，第一项为坐标（三维向量）

$D_Q$ 计算公式与 $D_P$ 同理。

最终结构化特征提取出来两个11维向量，包含了点云的内部特征（差分向量、点对特征、坐标）和外部特征（角度）

2、特征提取

特征提取部分，输入两个11维向量 $D_Q$ 和 $D_P$ ，经结构化Embedding后得到 $N \times d_e$ 维的向量 $F_P^e$ 和 $M \times d_e$ 维的向量 $F_Q^e$ ，然后经过结构注意力机制，得到同样维度的 $F_P^o$ 和 $F_Q^o$ 。

结构化Embedding：通过结构化特征提取出的内部和外部特征，来作隐式位置编码，替代传统如Geotransformer中的显式几何编码，更好的利用点云中的无序性来构建点云结构的一致性。

结构注意力机制：在原有的transformer结构中取消了位置编码，并引入了对应的点云，对两点云进行结构一致性关系进行挖掘，在最终的加权求和也多了对应点云侧枝的权重：

结构注意力机制如下：

3、点云匹配

使用可学习的RPM来提取对应关系，使用退火方式的β参数和软分配的α参数来进行软分配，而不是传统ICP算法的硬分配，通过概率分配来提高点云间的模糊性和不确定性，提高系统鲁棒性。

RPM算法就是将任意一个源点云中的点，建立与模板点云间点的对应关系，并对任意点对赋予0到1的值，并通过最小化，最终收敛到0或1,其中1为对应，0为完全不对应。对应赋值如下：

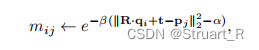
经过上述RPM算法工作后得到一个预匹配矩阵M，此时利用可微分的Sinkhorn算法对预匹配矩阵进行交替的行和列的归一化，来尽可能满足双随机矩阵约束条件，即任意一行或一列的元素和为1，保证点云匹配矩阵是完全软分配的。

4、变换估计

利用已生成的匹配矩阵来构建伪点对，依照模板点云计算新模板点云，将新模板点云作为源点云，用于损失计算。

5、损失函数

损失函数由三个部分组成：点匹配变换损失 $L_{trans}$ 、配准全局对应损失 $L_{corr}$ 、匹配矩阵匹配损失 $L_{match}$ 。

$L_{trans}$ ：针对于模板点云计算真实值的变换与预测的变换之间的误差关系。

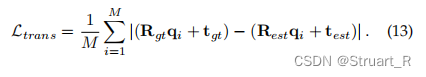
$L_{corr}$ ：计算模板点云相较于源点云之间的误差和源点云相较于模板点云之间的误差

$L_{match}$ ：为了解决离群点问题，计算匹配矩阵的损失作为惩罚项

总损失 $L_{total}$ ：其中 $N$ 为迭代次数。

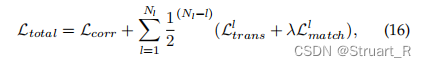
四、实验

1、数据集

使用合成数据集ModelNet40以及真实场景数据集3DMatch和KITTI进行测试。

2、评估指标

使用均方根误差RMSE、平均绝对误差MAE、相对误差ERROR和其中ERROR（R）计算旋转距离，ERROR（t）计算平移距离。

3、细节

在不可见物体、不可见类别、高斯噪音相较于SOTA都有较好的提升，部分重叠情况相较于RGM有较好的提升，但GeoTransformer这种依赖显式点云位置编码的效果更优。

4、对比实验

在结构化特征子、结构注意力机制、大旋转点云的鲁棒性问题上进行对比实验，证明了EGST模型的稳定性。