48.旋转图像

规律：

对于矩阵中第 i行的第 j 个元素，在旋转后，它出现在倒数第i 列的第 j 个位置。

matrix[col][n−row−1]=matrix[row][col]

可以使用辅助数组，如果不想使用额外的内存，可以用一个临时变量 。

 

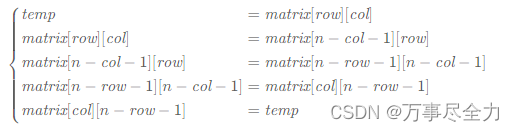
还可以通过水平翻转后再进行主对角线翻转。

class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix.length;
        // 水平翻转
        for(int i=0; i<n/2; i++){
            for(int j=0; j<n; j++){
                int temp = matrix[i][j];
                matrix[i][j]=matrix[n-i-1][j];
                matrix[n-i-1][j]=temp;
            }
        }
        // 主对角线翻转
        for(int i=0; i<n; i++){
            for(int j=0; j<i; j++){
                int temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i]=temp;
            }
        }
    }
}

240.搜索二维矩阵 II

由于矩阵 matrix中每一行的元素都是升序排列的，因此我们可以对每一行都使用一次二分查找，判断 target 是否在该行中，从而判断 target 是否出现。

也可以采用Z字形查找。

从矩阵 matrix的右上角 (0,n−1)进行搜索。在每一步的搜索过程中，如果我们位于位置 (x,y)，那么我们希望在以 matrix 的左下角为左下角、以 (x,y)为右上角的矩阵中进行搜索，即行的范围为 [x,m−1]，列的范围为 [0,y]。

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int m = matrix.length, n = matrix[0].length;
        int x=0, y=n-1;
        while(x<m && y>=0){
            if(matrix[x][y]==target){
                return true;
            }
            if(matrix[x][y]<target){
                x++;
            }else{
                y--;
            }
        }
        return false;
    }
}