1、aubo arcs sdk poseInverse 使用例子
auto cur_pose = rpc_cli->getRobotInterface(robot_name)
->getRobotState()
->getTcpPose();
// 2.288083 0.035207 1.550335
auto pose_inv = rpc_cli->getMath()
->poseInverse(cur_pose);
//结果:0.118611 -0.576932 -0.273097 -3.082975 -0.852550 1.539719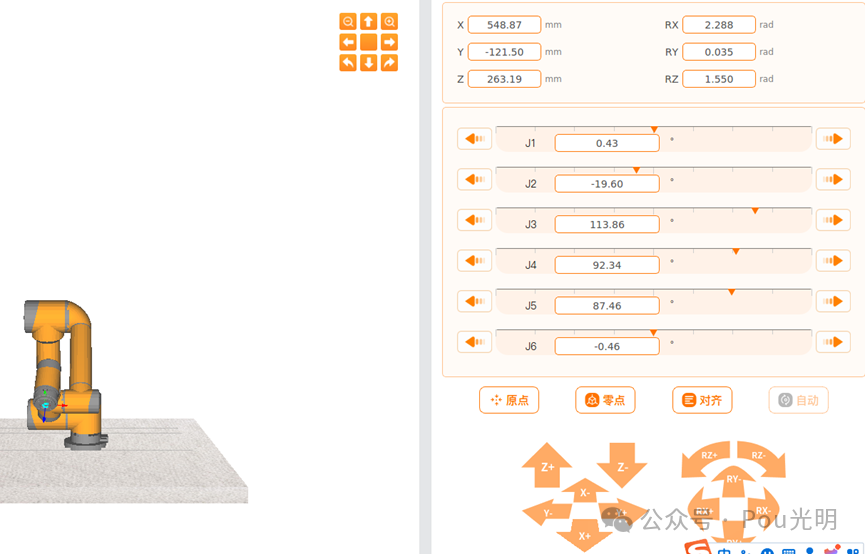
2、位姿逆变换
1>UR机械臂脚本手册
pose_inv(p_from)
获取姿态的反向。
参数
p_from:工具姿态(空间矢量)
返回值
使工具姿态变换反向(空间矢量)
2>《机器人学导论》变换算法-逆变换
已知坐标系{B}相对于坐标系{A}——即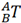 的值已知。有时为了得到{A}相对于{B}的描述,即
的值已知。有时为了得到{A}相对于{B}的描述,即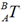 ,需要求该矩阵的逆。一个直接求逆的方式是将4×4齐次变换求逆。但是,这样做就不能充分利用变换的性质。容易看出比较简单的方法是利用变换的性质求逆。
,需要求该矩阵的逆。一个直接求逆的方式是将4×4齐次变换求逆。但是,这样做就不能充分利用变换的性质。容易看出比较简单的方法是利用变换的性质求逆。
为了求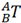 ,必须由
,必须由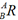 和
和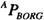 求出
求出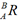 和
和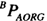 。首先,回顾一下关于旋转矩阵的结论:
。首先,回顾一下关于旋转矩阵的结论:


之后利用2-13将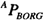 转变成在{B}中的描述:
转变成在{B}中的描述:

式2-43的左边应为0,由此可得:
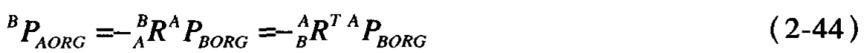
由2-42和2-44可写出:

注意,使用符号:
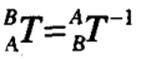
式2-45是求齐次逆变换一般且非常有用的方法。
3、eigen库求位姿的逆
直接代码:
Eigen::Vector3d euler_angle(2.288083, 0.035207, 1.550335);
// 使用Eigen库将欧拉角转换为旋转矩阵
Eigen::Matrix3d RBA;
RBA = Eigen::AngleAxisd(euler_angle[2], Eigen::Vector3d::UnitZ()) *
Eigen::AngleAxisd(euler_angle[1], Eigen::Vector3d::UnitY()) *
Eigen::AngleAxisd(euler_angle[0], Eigen::Vector3d::UnitX());
cout << "RBA is :\n" << RBA << std::endl;
cout << "RBA 转置 is :\n" << RBA.transpose() << std::endl;
Eigen::Matrix3d R = RBA.transpose();
Eigen::Vector3d rpy = rotationMatrixToEulerAngles(R); // roll,pitch,yaw
cout << "roll_2 pitch_2 yaw_2 = " << rpy[0] << " " << rpy[1]
<< " " << rpy[2] << endl;
Eigen::MatrixXd current_pos(3,1);
current_pos(0,0)= 0.582681;
current_pos(1,0)= -0.121500;
current_pos(2,0)= 0.259270;
Eigen::MatrixXd inv_pos(3,1);
Eigen::Matrix<double, 3, 1> m3x1;
m3x1 = -R*current_pos;
cout << "m3x1 is :\n" << m3x1 << std::endl;旋转的逆是其转置矩阵。
Sdk 结果:0.118611 -0.576932 -0.273097 -3.082975 -0.852550 1.539719
结果如图:
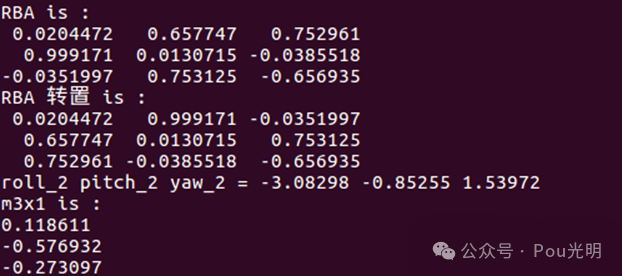
好了,本次笔记到此结束。
记徐先生到常州溧阳一游,超人结婚。假期前两天心情异常平静。
欢迎关注:

坚持探索!