图神经网络实战(13)——经典链接预测算法
- 0. 前言
- 1. 链接预测
- 2. 启发式技术
- 2.1 局部启发式技术
- 2.2 全局启发式技术
- 3. 矩阵分解
- 小结
- 系列链接
0. 前言
链接预测 (Link prediction) 可以帮助我们理解和挖掘图中的关系,并在社交网络、推荐系统等领域提供更准确的预测和决策支持。为了解决链接预测问题,研究者们提出了多种方法。首先,本节将介绍基于局部和全局邻域的启发式方法。然后,我们将介绍矩阵分解及其与 DeepWalk 和 Node2Vec 的联系。
1. 链接预测
链接预测 (Link prediction,也称链路预测)是图学习中的常见任务之一,用于预测两个节点之间是否存在链接的问题。链接预测是社交网络和推荐系统的核心,例如,在社交网络中,链接预测可以用于发现潜在的朋友关系、推荐共同的兴趣爱好,或者预测用户之间的互动行为。直观地说,如果存在链接的可能性很高,就更有可能与这些人建立联系,这种可能性正是链接预测试图预测的内容。
2. 启发式技术
启发式技术 (Heuristic technique) 是一种简单实用的预测节点之间链接的方法。它们易于实现,并为连接预测任务提供了强大的基准。根据这些方法执行的跳数 (hop),我们可以将它们进行分类,如下图所示。其中一些方法只需要与目标节点相邻的 1 跳 (1-hop) 邻居,而更复杂的技术还需要考虑 2 跳 (1-hop) 邻居或整个图。在本节中,我们将把它们分为两类——局部 (local) 启发式(1 跳和 2 跳)技术和全局 (global) 启发式技术。

2.1 局部启发式技术
局部启发式技术通过考虑节点的局部邻域来衡量两个节点之间的相似性,使用 N ( u ) \mathcal N(u) N(u) 表示节点 u u u 的邻居。以下是三种常用的局部启发式技术:
- 公共邻居 (
Common neighbors):简单地计算两个节点的公共邻居(1 跳邻居)数量。其原理与社交网络类似——共同的邻居越多,就越有可能建立链接:
f ( u , v ) = ∣ N ( u ) ∩ N ( v ) ∣ f(u,v)=|\mathcal N(u)\cap \mathcal N(v)| f(u,v)=∣N(u)∩N(v)∣ Jaccard 系数(Jaccard’s coefficient):衡量的是两个节点(1 跳邻居)共有邻居的比例。它的理念与共同邻居相同,但将结果按邻居总数归一化。这样可以奖励具有少量相互连接的邻居的节点,而非度较高的节点:
f ( u , v ) = ∣ N ( u ) ∩ N ( v ) ∣ ∣ N ( u ) ∪ N ( v ) ∣ f(u,v)=\frac {|\mathcal N(u)\cap \mathcal N(v)|} {|\mathcal N(u)\cup \mathcal N(v)|} f(u,v)=∣N(u)∪N(v)∣∣N(u)∩N(v)∣Adamic–Adar 指数(Adamic–Adar index):对两个目标节点(2 跳邻居)共享邻居度数的逆对数求和。其原理是,邻域大的共同邻居不如邻域小的共同邻居重要:
f ( u , v ) = ∑ x ∈ N ( u ) ∩ N ( v ) 1 l o g ∣ N ( x ) ∣ f(u,v)=\sum_{x\in\mathcal N(u)\cap \mathcal N(v)}\frac 1{log|\mathcal N(x)|} f(u,v)=x∈N(u)∩N(v)∑log∣N(x)∣1
无论是直接的(共同邻居或Jaccard 系数)还是间接的(Adamic–Adar 指数) ,这些技术都依赖于邻居的节点度。这有利于提高速度和可解释性,但也限制了它捕捉复杂关系的能力。
2.2 全局启发式技术
全局启发式技术通过考虑整个网络而非局部邻域来解决这一问题。以下是两种常用的全局启发式技术:
Katz 指数(Katz index):计算两个节点之间每条可能路径的加权和。权重对应一个折扣系数 β ∈ [ 0 , 1 ] β∈ [0,1] β∈[0,1] (通常在0.8到0.9之间),以惩罚较长的路径。根据这一定义,如果两个节点之间有很多(最好是短)路径,那么它们更有可能被连接起来。任何长度的路径都可以用邻接矩阵幂 A n A^n An 计算,Katz 指数定义如下:
f ( u , v ) = ∑ i = 1 ∞ β i A i f(u,v)=\sum_{i=1}^\infty\beta^iA^i f(u,v)=i=1∑∞βiAi- 带重启的随机游走 (
Random walk with restart):从目标节点开始进行随机游走。每次游走后,它会增加当前节点的访问次数,并以 α α α 的概率在目标节点重新开始游走。否则,它会继续随机游走。经过预定的迭代次数后停止算法,并建议在目标节点和访问次数最高的节点之间建立链接。这种思想在 DeepWalk 和 Node2Vec 算法中同样重要
全局启发式技术通常更准确,但需要了解图的全部内容,使用这种方式执行链接预测并不是唯一方法。
3. 矩阵分解
用于链接预测的矩阵分解 (Matrix factorization) 受到推荐系统技术的启发。使用这种技术,我们通过预测整个邻接矩阵 KaTeX parse error: Undefined control sequence: \A at position 1: \̲A̲ 来间接预测链接。这需要使用节点嵌入来实现——相似的节点
u
u
u 和
v
v
v 应该有相似的嵌入
Z
u
Z_u
Zu 和
Z
v
Z_v
Zv。利用点积,我们可以将其表示为:
- 如果这些节点相似, Z v T Z u Z_v^TZ_u ZvTZu 应该是最大的
- 如果这些节点不同, Z v T Z u Z_v^TZ_u ZvTZu 应该是最小的
由于我们假定相似的节点应该相互连接,因此可以使用点积来近似邻接矩阵
A
A
A 的每个元素(链接):
A
u
v
≈
Z
v
T
Z
u
A_{uv}\approx Z_v^TZ_u
Auv≈ZvTZu
改写为矩阵乘法,可以得到以下结果:
A
≈
Z
T
Z
A\approx Z^TZ
A≈ZTZ
其中,
Z
Z
Z 是节点嵌入矩阵。下图直观地说明了矩阵分解的原理:
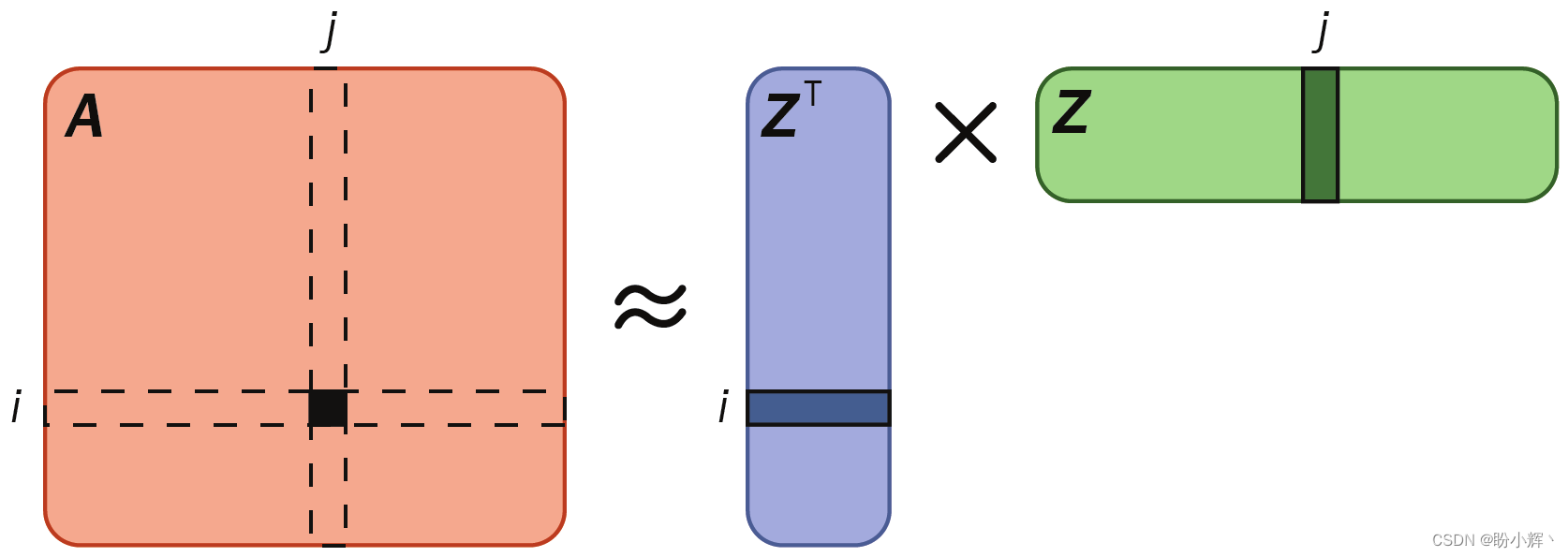
这种技术之所以称为矩阵分解,是因为邻接矩阵
A
A
A 被分解为两个矩阵的乘积。其目标是学习相关的节点嵌入,使图
G
=
(
V
,
E
)
G= (V,E)
G=(V,E) 中真实元素和预测元素之间的 L2 范数
A
u
v
A_{uv}
Auv 最小化:
m
i
n
z
∑
i
∈
V
,
j
∈
V
(
A
u
v
−
Z
v
T
Z
u
)
2
\underset {z} {min}\sum_{i\in V,j\in V}(A_{uv}-Z_v^TZ_u)^2
zmini∈V,j∈V∑(Auv−ZvTZu)2
矩阵分解还有更高级的变体,包括拉普拉斯矩阵 (Laplacian matrix) 和
A
A
A 的幂,另一种方法是使用 DeepWalk 和 Node2Vec 等模型,它们能够生成可以配对创建链接表示的节点嵌入,这些算法隐式地逼近和分解复杂的矩阵。例如,使用 DeepWalk 计算出的矩阵:
log
(
∑
i
=
1
∣
V
∣
∑
j
=
1
∣
V
∣
A
i
j
(
1
T
∑
r
=
1
T
(
D
−
1
A
)
r
)
D
−
1
)
−
log
b
\log (\sum_{i=1}^{|V|}\sum_{j=1}^{|V|}A_{ij}(\frac 1T\sum_{r=1}^T(D^{-1}A)^r)D^{-1})-\log b
log(i=1∑∣V∣j=1∑∣V∣Aij(T1r=1∑T(D−1A)r)D−1)−logb
其中,
b
b
b 是负采样的参数。类似算法包括 LINE 和 PTE。虽然它们可以捕捉到更复杂的关系,但也存在局限性:
- 无法使用节点特征:只能使用拓扑信息创建嵌入关系
- 没有归纳能力: 无法归纳出训练集中没有的节点
- 无法捕捉结构相似性: 图中结构相似的节点能够获得截然不同的嵌入结果
这些局限性促使我们需要基于图神经网络 (Graph Neural Networks, GNN) 的技术来执行链接预测任务。
小结
链接预测是指利用图数据中已知的部分节点和边的信息,预测图中未知的连接关系或者未来可能出现的连接关系。链接预测在社交网络分析、生物信息学、推荐系统等领域具有重要应用,能够帮助我们理解网络结构、预测潜在的关联关系,并为一些实际问题提供决策支持。在本节中,我们介绍了经典链接预测算法,这些传统技术对于理解图神经网络 (Graph Neural Networks, GNN) 学习的内容至关重要。
系列链接
图神经网络实战(1)——图神经网络(Graph Neural Networks, GNN)基础
图神经网络实战(2)——图论基础
图神经网络实战(3)——基于DeepWalk创建节点表示
图神经网络实战(4)——基于Node2Vec改进嵌入质量
图神经网络实战(5)——常用图数据集
图神经网络实战(6)——使用PyTorch构建图神经网络
图神经网络实战(7)——图卷积网络(Graph Convolutional Network, GCN)详解与实现
图神经网络实战(8)——图注意力网络(Graph Attention Networks, GAT)
图神经网络实战(9)——GraphSAGE详解与实现
图神经网络实战(10)——归纳学习
图神经网络实战(11)——Weisfeiler-Leman测试
图神经网络实战(12)——图同构网络(Graph Isomorphism Network, GIN)