文章目录
- 1. Ax=b下的最值问题-图形转换
- 2. Gram-Schmidt 标准形
- 3. 迭代法-Krylov子空间法
1. Ax=b下的最值问题-图形转换
假设我们有一个直线方程如下:
3
x
1
+
4
x
2
=
1
\begin{equation} 3x_1+4x_2=1 \end{equation}
3x1+4x2=1
在二维平面上,各个范数如下:
min
∣
∣
x
∣
∣
1
=
∣
x
1
∣
+
∣
x
2
∣
,
min
∣
∣
x
∣
∣
2
=
x
1
2
+
x
2
2
,
min
∣
∣
x
∣
∣
∞
=
max
∣
x
i
∣
\begin{equation} \min||x||_1=|x_1|+|x_2|,\min||x||_2=x_1^2+x_2^2,\min||x||_{\infty}=\max|x_i| \end{equation}
min∣∣x∣∣1=∣x1∣+∣x2∣,min∣∣x∣∣2=x12+x22,min∣∣x∣∣∞=max∣xi∣
- L1范数是一个膨胀的钻石形状,L2范数是一个膨胀的圆形,
L
∞
L_{\infty}
L∞是一个膨胀的正方形

- 那么在Ax=b约束条件下的最小值问题可以转换为范数图像与约束条件 A x = b Ax=b Ax=b组成图像的第一个相交的点。
- L1与直线相交A点,L2与直线相交B点,L3与直线相交C点,这样就可以通过几何图形的方式求得在约束条件下的最小值问题了,用函数图像代替约束条件方程Ax=b,用范数表示不同情况下的最值问题。真神奇!!!

2. Gram-Schmidt 标准形
通过Gram-Schmidt 可以将矩阵A分解如下
A
=
Q
R
A=QR
A=QR。
我们有一个矩阵A的列向量组,发现矩阵A的列向量之间不是相互正交的,如果列向量之间不是相互正交独立,那么就无法用最简单的形式去表达其他的向量,所以我们就用Gram-Schmidt,将原来的
a
1
,
a
2
a_1,a_2
a1,a2转换成
q
1
,
q
2
,
q
1
⊥
q
2
,
∣
q
1
∣
=
∣
q
2
∣
=
1
q_1,q_2,q_1\perp q_2,|q_1|=|q_2|=1
q1,q2,q1⊥q2,∣q1∣=∣q2∣=1 ,Gram-Schmidt用的方法很简单,
- 先选择一个向量
a
1
a_1
a1,直接以这个向量作为第一个方向,正交化得到
q
1
q_1
q1
q 1 = a 1 ∣ a 1 ∣ , ∣ q 1 ∣ = 1 \begin{equation} q_1=\frac{a_1}{|a_1|},|q_1|=1 \end{equation} q1=∣a1∣a1,∣q1∣=1 - 现在
a
2
a_2
a2与
q
1
q_1
q1不正交,我们就要将
a
2
a_2
a2投影到
q
1
q_1
q1上得到投影向量
p
2
p_2
p2,再用
a
2
−
p
2
=
A
2
a_2-p_2=A_2
a2−p2=A2
q 1 T a 2 = ∣ q 1 ∣ ∣ a 2 ∣ cos θ = ∣ a 2 ∣ cos θ , a 2 在 q 1 上的投影长度出来了 \begin{equation} q_1^Ta_2=|q_1||a_2|\cos{\theta}=|a_2|\cos{\theta},a_2在q_1上的投影长度出来了 \end{equation} q1Ta2=∣q1∣∣a2∣cosθ=∣a2∣cosθ,a2在q1上的投影长度出来了 - 投影长度乘以单位向量得到
p
2
p_2
p2,向量相减得到
A
2
A_2
A2
p 2 = q 1 T a 2 q 1 , A 2 = a 2 − p 2 → A 2 = a 2 − q 1 T a 2 q 1 → q 2 = A 2 ∣ A 2 ∣ \begin{equation} p_2=q_1^Ta_2q_1,A_2=a_2-p_2\rightarrow A_2=a_2-q_1^Ta_2q_1\rightarrow q_2=\frac{A_2}{|A_2|} \end{equation} p2=q1Ta2q1,A2=a2−p2→A2=a2−q1Ta2q1→q2=∣A2∣A2 - 同理
q
3
q_3
q3就是将向量
a
3
a_3
a3减去
a
3
a_3
a3在
q
1
,
q
2
q_1,q_2
q1,q2上的投影向量
p
2
,
p
3
p_2,p_3
p2,p3即可得到
A
3
A_3
A3
p 3 = q 1 T a 3 q 1 , p 2 = q 2 T a 3 q 2 → A 3 = a 3 − q 1 T a 3 q 1 − p 2 = q 2 T a 3 q 2 \begin{equation} p_3=q_1^Ta_3q_1,p_2=q_2^Ta_3q_2\rightarrow A_3=a_3-q_1^Ta_3q_1-p_2=q_2^Ta_3q_2 \end{equation} p3=q1Ta3q1,p2=q2Ta3q2→A3=a3−q1Ta3q1−p2=q2Ta3q2
所以Gram-Schmidt的本质是从A中的列向量中不断抽取向量 a 1 , a 2 , ⋯ , a n a_1,a_2,\cdots,a_n a1,a2,⋯,an通过不断迭代的形式,得到一组标准正交向量组 q 1 , q 2 , ⋯ , q n q_1,q_2,\cdots,q_n q1,q2,⋯,qn, - 但我们发现一个问题,我们怎么选择向量
a
1
,
a
2
,
⋯
,
a
n
a_1,a_2,\cdots,a_n
a1,a2,⋯,an呢?如果
a
1
,
a
2
,
⋯
,
a
n
a_1,a_2,\cdots,a_n
a1,a2,⋯,an太相关了怎么办,这样正交化的效果不是很好,如下所示:我们希望选择好的向量
a
12
,
a
22
a_{12},a_{22}
a12,a22而不是相关性太大的
a
11
,
a
21
a_{11},a_{21}
a11,a21
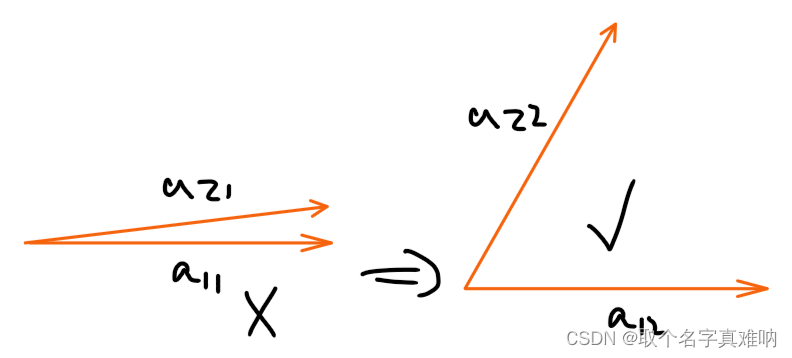
- 那怎么做了,我们只需要在每次选择新的向量的时候,选择投影p较小的向量作为正交向量,比如我们先找到 a 1 → q 1 a_1\rightarrow q_1 a1→q1再找 q 2 q_2 q2 过程中我们需要筛选,将 a 2 , a 3 , ⋯ , a n a_2,a_3,\cdots,a_n a2,a3,⋯,an都投影到 q 1 q_1 q1上,看看哪个投影长度最小,我们就选择这个作为 A 2 → q 2 A_2\rightarrow q_2 A2→q2
- 从
p
21
,
p
31
,
⋯
,
p
n
1
p_{21},p_{31},\cdots,p_{n1}
p21,p31,⋯,pn1中选择最小的一个作为
A
2
→
q
2
A_2\rightarrow q_2
A2→q2
p 21 = q 1 T a 2 q 1 , p 31 = q 1 T a 3 q 1 , ⋯ p n 1 = q 1 T a n q 1 \begin{equation} p_{21}=q_1^Ta_2q_1,p_{31}=q_1^Ta_3q_1,\cdots p_{n1}=q_1^Ta_nq_1 \end{equation} p21=q1Ta2q1,p31=q1Ta3q1,⋯pn1=q1Tanq1 - 同理依次选择
q
3
,
q
4
,
⋯
,
q
n
q_3,q_4,\cdots,q_n
q3,q4,⋯,qn,这就是改进后的
Gram-Schmidt
3. 迭代法-Krylov子空间法
- 背景: 当矩阵A太大并且稀疏情况下,我们需要用迭代的方法求解
A
x
=
b
Ax=b
Ax=b方程
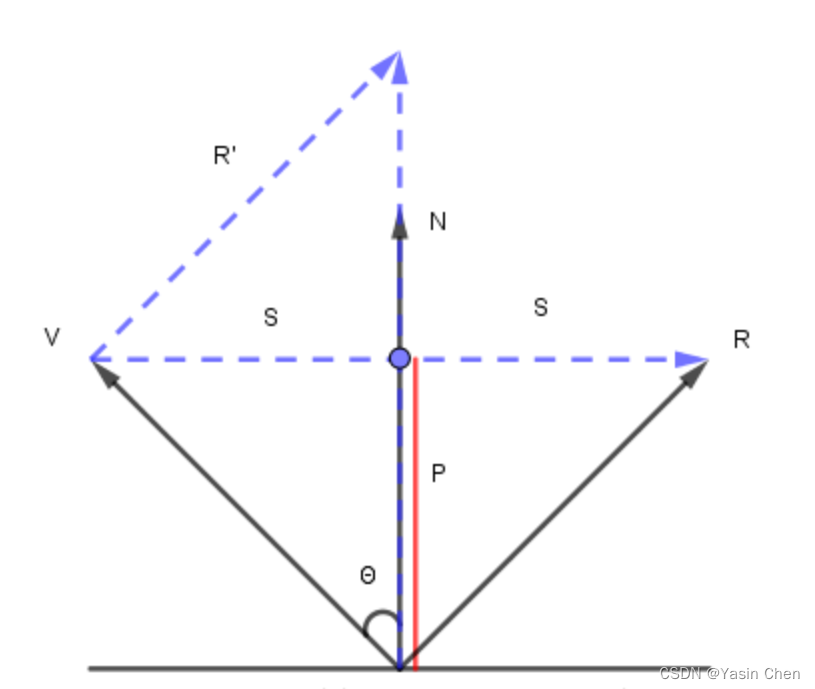
直接引用大神的笔记,具体后续整理






![[C][数据结构][树]详细讲解](https://img-blog.csdnimg.cn/direct/b84ce09c1a9644f595df76b866458cfa.png)