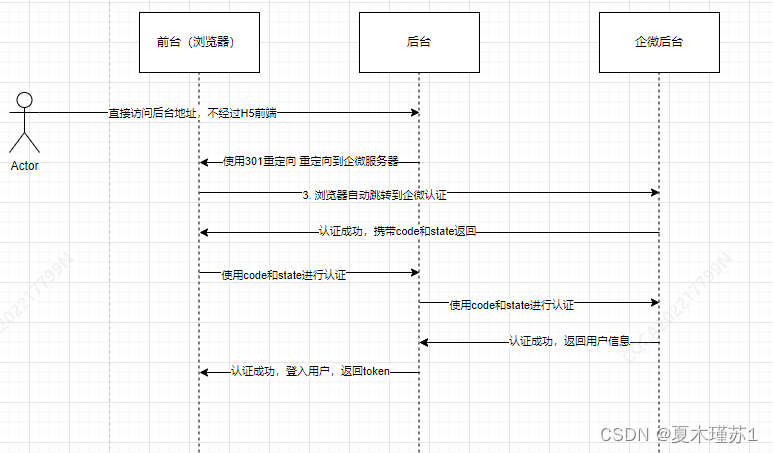
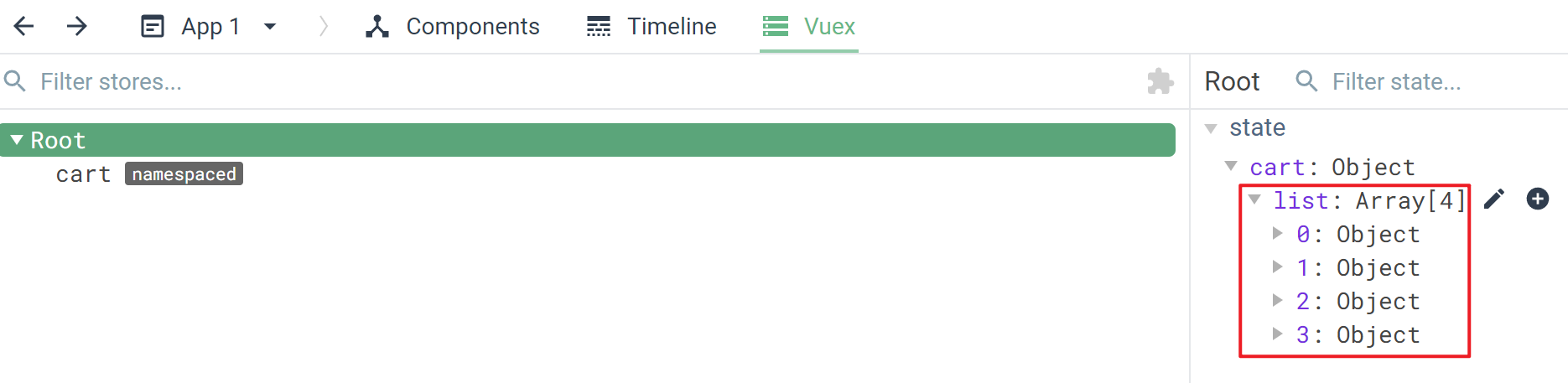
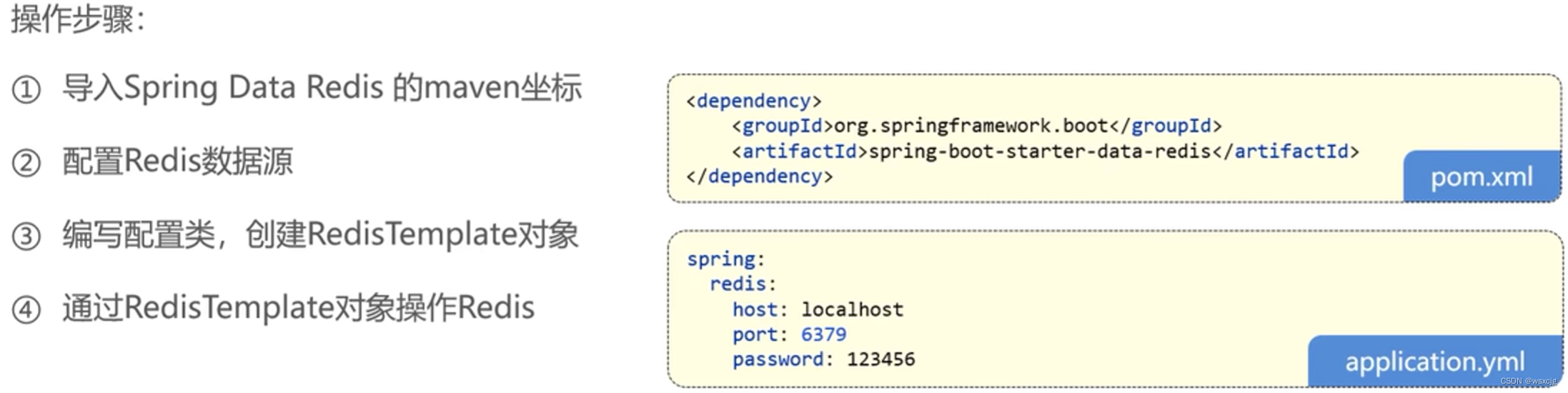
1 介绍

• 遗传算法有5个主要任务，直到找到最终的解决方案

2  举例

2.1 问题描述

• 比如我们有 5 个变量和约束，其中 X1、X2、X3、X4 和 X5 是非负整数且小于 10（0、1、2、4、5、6、7、8、9）
• 我们希望找到 X1、X2、X3、X4 和 X5 的最优解
  • 

2.2 解决方法

2.2.0 问题转化

• 将问题方程转化为目标函数。
  • 
• 遗传算法将尝试最小化目标函数以获得 X1、X2、X3、X4 和 X5 的解决方案。

2.2.1初始化

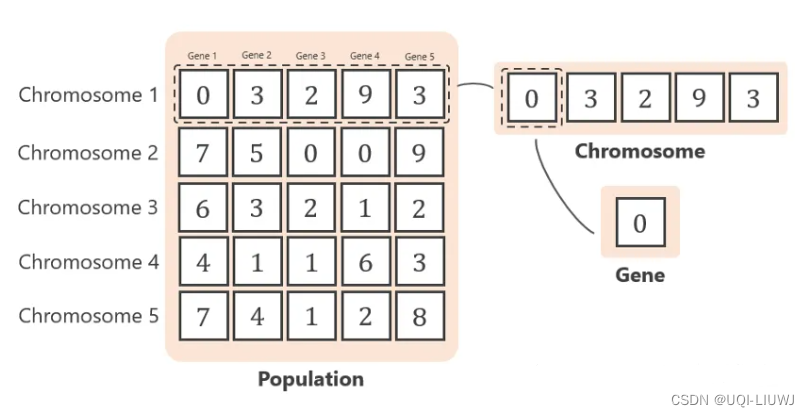
• 在初始化时，确定每一代的染色体数。
  • 我们记染色体的数量是 5。（一个种群有5条染色体）
  • 每个染色体有 5 个基因（X1~X5)，使用 0 到 9 之间的随机数生成基因。

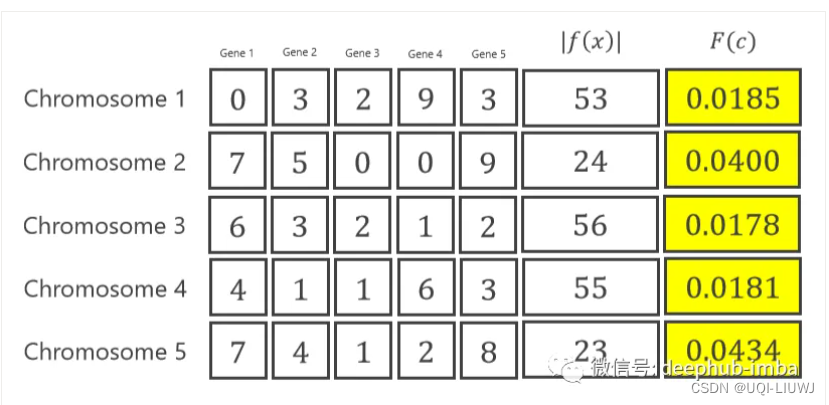
2.2.2 适应度函数计算（评估） 

• 将 X1、X2、X3、X4 和 X5 代入目标函数
  • 
• 适应度函数是 1 除以误差，其中误差为 (1 + f(x))
  • 分母+1是为了避免除零问题
  • 
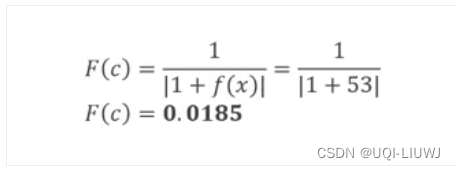
• ——>得到这个种群每个染色体的适应度
  • 

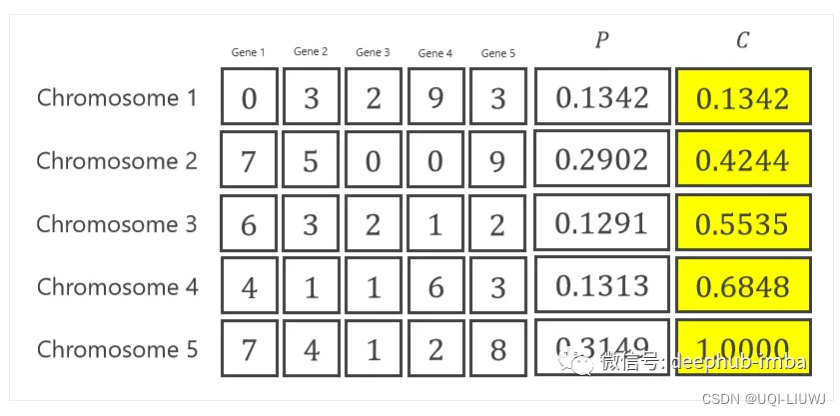
2.2.3  选择

• 在遗传算法的背景下，具有较高适应度值的染色体将更有可能在轮盘赌中被选中
• 计算 5 条染色体的总适应度值，然后计算每条染色体适应度的占比（每个染色体的概率）
  • 
• 接着计算累积概率
  • 
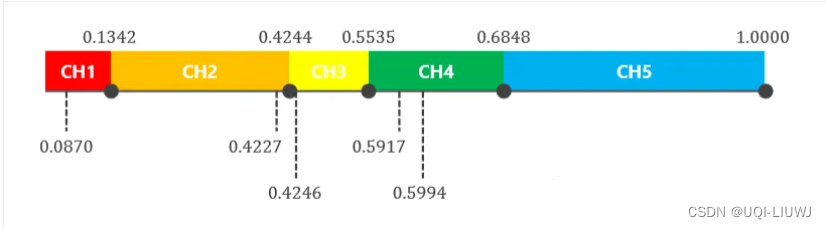
• 然后生成5个随机数Uniform(0,1)
  • 这些随机数决定了选择哪几条染色体（可以重复选一条）
  • 比如选择了：
    • 
    • 找到对应概率区间的那条染色体
      • 
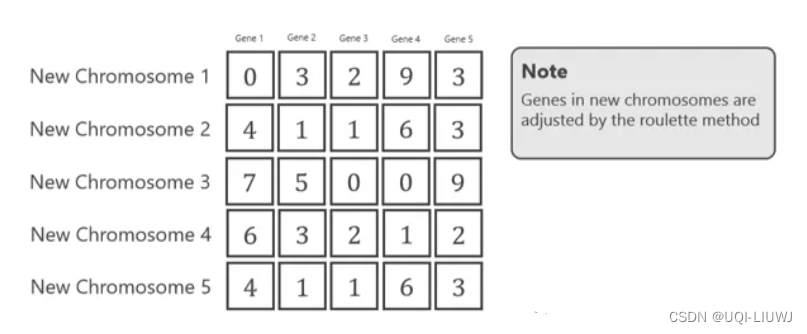
  • ——>选择后的新染色体：
    • 

2.2.4 交叉

• 在生物学中，交叉是指生殖的一个术语。两条染色体被随机选择并通过数学运算进行匹配。
• 这里简单起见，使用单点交叉
  • 首先我们事先确定好交叉率(Pc)【比如为0.25】
    • 下面随机数目小于0.25的染色体将成为交叉中的亲本
  • 然后生成5个Uniform(0,1)分布的随机数
    • 
    • 小于0.25的三个对应的染色体是1，3，5，将他们结合（编号小的在前面）
      • 
• 但此时我们只是知道了哪几个染色体交叉，那么从哪个位置开始交叉呢
  • 为了确定交叉线的位置，需要生成一个1到n之间的随机数，其中n是染色体- 1的长度
    • 
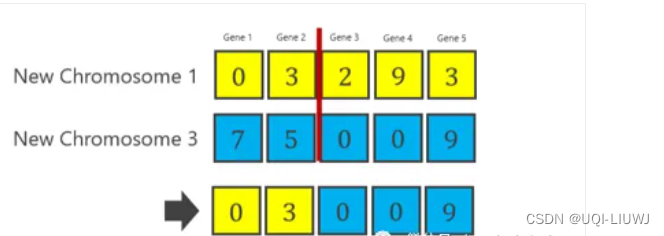
    • ——>染色体1&3 之间的交叉
      • 
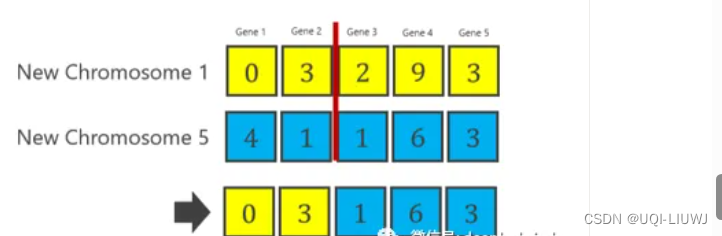
    • ——>1和5号染色体之间的交叉
      • 
    • ——>3号和5号染色体
      • 

2.2.5 突变

• 突变是赋予任何基因新价值的过程
• 事先确定突变率Pm
• 首先计算一个种群中的基因数量
  • 基因总数 = 染色体 x 染色体中的基因数
  • ——>这里是3
• 然后我们生成3个1~种群基因数的随机数，这些位置就是基因突变的位置
  • 对于每一个被选中的基因，生成一个从0到9的随机数来替换旧的值
  • 

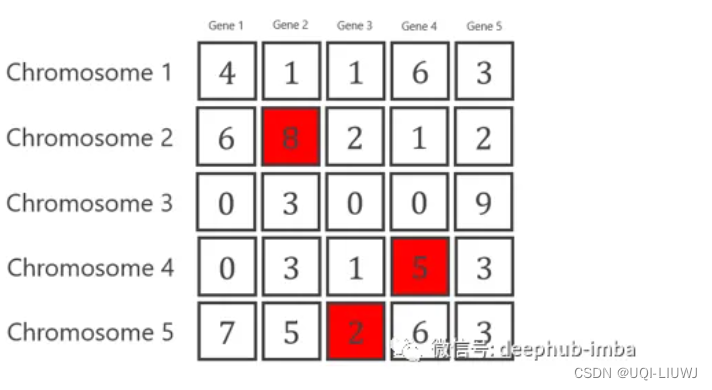
——>这就是第二代染色体了

使用生成的新一代重复这个过程，就可以以获得X1、X2、X3、X4和X5的最佳解

参考内容：手推遗传算法（Genetic Algorithm，GA）的详细步骤图解 (qq.com)