【Python深度学习】——信息量|熵
- 假设
- 1. 信息量
- 1.1 含义
- 1.2 信息量的公式:
- 2. 熵Entropy
- 2. 含义
- 2.2 熵的计算公式:
- 2.3 熵的作用
假设
例子:掷硬币
假设我们有一个公平的硬币。这个硬币有两个面:正面(H)和反面(T),每次掷硬币出现正面或反面的概率都是 0.5
1. 信息量
1.1 含义
信息量用来表示一件事发生的难易程度
一件事越容易发生, 它的信息量就越小.
1.2 信息量的公式:
I
(
x
)
=
−
log
2
P
(
x
)
\ I(x) = -\log_2 P(x) \
I(x)=−log2P(x)
其中,
I
(
x
)
\ I(x) \
I(x) 表示事件 ( x ) 的信息量,
P
(
x
)
\ P(x)
P(x)表示事件 ( x ) 发生的概率
以2为底, 是转换到二进制下的表示复杂度.
此外, 事件独立时, 两个事件同时发生的信息量,等于两个事件的信息量相加.
即
I
(
A
B
)
=
−
log
2
1
P
(
A
B
)
=
−
log
2
1
P
(
A
)
∗
P
(
B
)
=
−
(
log
2
1
P
(
A
)
+
log
2
1
P
(
B
)
)
=
I
(
A
)
+
I
(
B
)
\ I(AB)= -\log_2 \frac{1}{P(AB)} = -\log_2 \frac{1}{P(A)*P(B)} = -(\log_2 \frac{1}{P(A)}+ \log_2 \frac{1}{P(B)}) =I(A) + I(B) \
I(AB)=−log2P(AB)1=−log2P(A)∗P(B)1=−(log2P(A)1+log2P(B)1)=I(A)+I(B)
对于假设中的例子, 出现正面的信息量为:
I
(
H
)
=
−
log
2
P
(
H
)
=
−
log
2
0.5
=
1
bit
I(H) = -\log_2 P(H) = -\log_2 0.5 = 1 \text{ bit}
I(H)=−log2P(H)=−log20.5=1 bit
同理反面也是
I
(
T
)
=
−
log
2
P
(
T
)
=
−
log
2
0.5
=
1
bit
I(T) = -\log_2 P(T) = -\log_2 0.5 = 1 \text{ bit}
I(T)=−log2P(T)=−log20.5=1 bit
2. 熵Entropy
2. 含义
熵可以理解为一个整体/一个系统所携带的信息量.
系统整体由所有可能发生的事件构成. 例如, 抛硬币的结果出现正面和反面就构成一个完整的系统.
熵的值就等于概率分布中所有信息量的期望.
2.2 熵的计算公式:
H
(
x
)
=
−
∑
i
P
(
x
i
)
log
2
P
(
x
i
)
H(x) = - \sum_{i} P(x_i) \log_2 P(x_i)
H(x)=−i∑P(xi)log2P(xi)
对于假设中的例子, 熵的计算为:
H
(
X
)
=
−
[
P
(
H
)
log
2
P
(
H
)
+
P
(
T
)
log
2
P
(
T
)
]
H(X) = -\left [P(H) \log_2 P(H) + P(T) \log_2 P(T) \right]
H(X)=−[P(H)log2P(H)+P(T)log2P(T)]
即,
H
(
X
)
=
−
[
0.5
log
2
0.5
+
0.5
log
2
0.5
]
H(X) = -\left[ 0.5 \log_2 0.5 + 0.5 \log_2 0.5 \right]
H(X)=−[0.5log20.5+0.5log20.5]
H ( X ) = − [ 0.5 ⋅ ( − 1 ) + 0.5 ⋅ ( − 1 ) ] H(X) = -\left[ 0.5 \cdot (-1) + 0.5 \cdot (-1) \right] H(X)=−[0.5⋅(−1)+0.5⋅(−1)]
H ( X ) = 1 H(X) = 1 H(X)=1
2.3 熵的作用
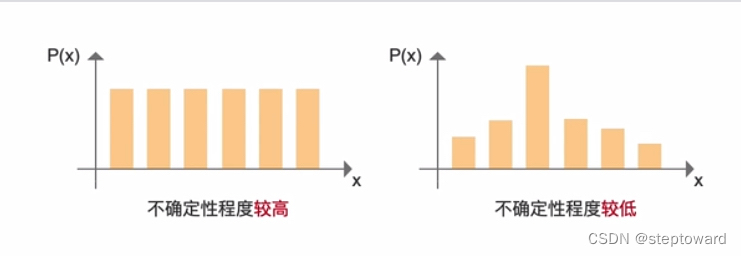
熵可以用来评估概率模型的不确定性程度——概率密度越均匀, 不确定性越高,即熵越高; 概率密度越聚拢, 不确定性越低, 熵越低.
如下图所示,左图为一个平均分布, 不确定性较高;
右图为一个正太分布, 不确定性较低.