北航第五次数据结构与程序设计编程题复习
- 树叶节点遍历(树-基础题)
- 计算器(表达式计算-表达式树实现)
- 服务优化
- 词频统计(树实现)
树叶节点遍历(树-基础题)
【问题描述】
从标准输入中输入一组整数,在输入过程中按照左子结点值小于根结点值、右子结点值大于等于根结点值的方式构造一棵二叉查找树,然后从左至右输出所有树中叶结点的值及高度(根结点的高度为1)。例如,若按照以下顺序输入一组整数:50、38、30、64、58、40、10、73、70、50、60、100、35,则生成下面的二叉查找树:
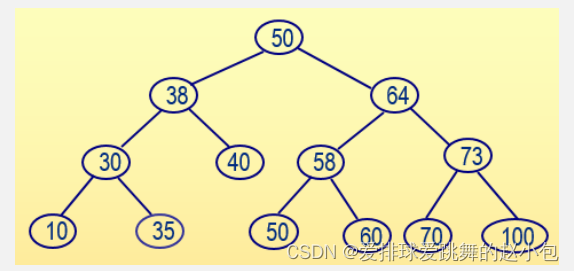 从左到右的叶子结点包括:10、35、40、50、60、70、100,叶结点40的高度为3,其它叶结点的高度都为4。
从左到右的叶子结点包括:10、35、40、50、60、70、100,叶结点40的高度为3,其它叶结点的高度都为4。
【输入形式】
先从标准输入读取整数的个数,然后从下一行开始输入各个整数,整数之间以一个空格分隔。
【输出形式】
按照从左到右的顺序分行输出叶结点的值及高度,值和高度之间以一个空格分隔。
【样例输入】
13
50 38 30 64 58 40 10 73 70 50 60 100 35
【样例输出】
10 4
35 4
40 3
50 4
60 4
70 4
100 4
【样例说明】
按照从左到右的顺序输出叶结点(即没有子树的结点)的值和高度,每行输出一个。
【评分标准】
该题要求输出所有叶结点的值和高度,提交程序名为:bst.c
这个题的大体框架就是逐点插入法,但是要多做一步:结点结构体中多加一项元素deep,用于存放节点的深度。结点插入时,每和已有树中结点比较一次,deep加一。
题目要求从左往右打印叶子结点,其实就是中序遍历的思想。但实际上,中间的根结点不可能是需要访问的叶子结点(你都是根了肯定有子节点啊),因此只需要先遍历左子树再右子树就可以了。
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
typedef struct node
{
int val;
int deep;
struct node*left;
struct node*right;
}BTNode;
BTNode* root=NULL;
void insert(int);
void leaf(BTNode*);
int main()
{
int n,item;
scanf("%d",&n);
for(int i=0;i<n;i++)
{
scanf("%d",&item);
insert(item);
}
leaf(root);
}
void insert(int item)
{
BTNode* new=(BTNode*)malloc(sizeof(BTNode));
new->deep=1;
new->left=new->right=NULL;
new->val=item;
if(root==NULL)
{
root=new;
return;
}
BTNode* cur=root;
while(1)
{
if(item<cur->val)
{
new->deep++;
if(cur->left==NULL)
{
cur->left=new;
break;
}
else
cur=cur->left;
}
else if(item>=cur->val)
{
new->deep++;
if(cur->right==NULL)
{
cur->right=new;
break;
}
else
cur=cur->right;
}
}
}
void leaf(BTNode* root)
{
if(root==NULL)
return;
if(root->left==NULL&&root->right==NULL)
printf("%d %d\n",root->val,root->deep);
leaf(root->left);
leaf(root->right);
}
计算器(表达式计算-表达式树实现)
【问题描述】
从标准输入中读入一个整数算术运算表达式,如24 / ( 1 + 2 + 36 / 6 / 2 - 2) * ( 12 / 2 / 2 )= ,计算表达式结果,并输出。
要求:
1、表达式运算符只有+、-、*、/,表达式末尾的=字符表示表达式输入结束,表达式中可能会出现空格;
2、表达式中会出现圆括号,括号可能嵌套,不会出现错误的表达式;
3、出现除号/时,以整数相除进行运算,结果仍为整数,例如:5/3结果应为1。
4、要求采用表达式树来实现表达式计算。
表达式树(expression tree):
我们已经知道了在计算机中用后缀表达式和栈来计算中缀表达式的值。在计算机中还有一种方式是利用表达式树来计算表达式的值。表达式树是这样一种树,其根节点为操作符,非根节点为操作数,对其进行后序遍历将计算表达式的值。由后缀表达式生成表达式树的方法如下:
l 读入一个符号:
l 如果是操作数,则建立一个单节点树并将指向他的指针推入栈中;
l 如果是运算符,就从栈中弹出指向两棵树T1和T2的指针(T1先弹出)并形成一棵新树,树根为该运算符,它的左、右子树分别指向T2和T1,然后将新树的指针压入栈中。
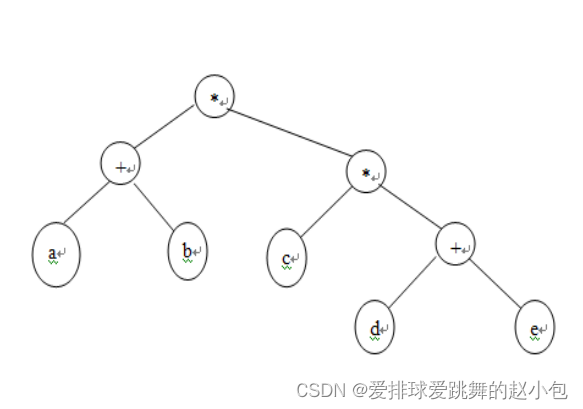
例如输入的后缀表达为:
ab+cde+**
则生成的表达式树为:
【输入形式】
从键盘输入一个以=结尾的整数算术运算表达式。操作符和操作数之间可以有空格分隔。
【输出形式】
首先在屏幕上输出表达式树根、左子节点及右子节点上的运算符或操作数,中间由一个空格分隔,最后有一个回车(如果无某节点,则该项不输出)。然后输出表达式计算结果。
【样例输入】
24 / ( 1 + 2 + 36 / 6 / 2 - 2) * ( 12 / 2 / 2 ) =
【样例输出】
- / /
18
【样例说明】
按照运算符及括号优先级依次计算表达式的值。在生成的表达树中,*是根节点的运算符,/ 是根节点的左子节点上运算符,/是根节点的右子节点上运算符,按题目要求要输出。
【评分标准】
通过所有测试点得满分。
我们之前用栈做过这个题,先把表达式转为逆波兰表达式,然后再计算,这次我们又多了一种办法:表达式树。
表达式树的特点是:叶结点是操作数,其他结点为操作符。
要构造表达式树,首先需要将表达式转化为后缀表达式。然后:
从左往右依次读入符号:
如果是操作数,则建立一个单节点树并将指向该节点的指针推入栈中
如果是运算符,则从栈中弹出两个树节点的指针并形成一棵新树,树根为运算符。然后将新树压入栈中。
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
enum set {OP,NUM};
typedef struct item
{
enum set type;
union
{
char ope;
int num;
}uni;
}ITEM;
typedef struct node
{
ITEM item;
int calnum;
struct node*left;
struct node*right;
}BTnode;
void remove_zero(char*);
void toReversePoland(char*);
int Priority(char);
void cal(ITEM*,int);
int main()
{
char arr[100];
gets(arr);
remove_zero(arr);
toReversePoland(arr);
return 0;
}
void remove_zero(char* a)
{
int i=0,j=0;
while(a[j]!='\0')
{
if(a[j]!=' ')
{
a[i]=a[j];
j++;
i++;
}
else
j++;
}
a[i]='\0';
}
void toReversePoland(char* a)
{
ITEM arr[100];
int index=0;
char operation[100];
int Top=-1;
for(int i=0;i<strlen(a);i++)
{
if(a[i]>='0'&&a[i]<='9')
{
int num=a[i]-'0';
for(int j=i+1;j<strlen(a);j++)
{
if(a[j]>='0'&&a[j]<='9')
{
num=num*10+(a[j]-'0');
}
else
{
arr[index].type=NUM;
arr[index].uni.num=num;
i=j-1;
index++;
break;
}
}
}
else if(a[i]=='=')
break;
else if(a[i]=='+'||a[i]=='-'||a[i]=='*'||a[i]=='/')
{
if(Top==-1)
operation[++Top]=a[i];
else
{
while(Top>-1&&operation[Top]!='('&&(Priority(operation[Top])>=Priority(a[i])))
{
arr[index].type=OP;
arr[index].uni.ope=operation[Top];
index++;
Top--;
}
operation[++Top]=a[i];
}
}
else if(a[i]=='(')
{
operation[++Top]='(';
}
else if(a[i]==')')
{
char top=operation[Top];
while(top!='(')
{
arr[index].type=OP;
arr[index].uni.ope=top;
index++;
Top--;
top=operation[Top];
}
Top--;
}
}
while(Top!=-1)
{
arr[index].type=OP;
arr[index].uni.ope=operation[Top];
index++;
Top--;
}
// for(int i=0;i<index;i++)
// {
// if(arr[i].type==OP)
// printf("%c ",arr[i].uni.ope);
// else
// printf("%.2f ",arr[i].uni.num);
// }
cal(arr,index);
}
int Priority(char a)
{
if(a=='+'||a=='-')
return 1;
if(a=='*'||a=='/')
return 2;
}
void cal(ITEM* arr,int n)
{
BTnode* stack[100];
int top=0;
for(int i=0;i<n;i++)
{
if(arr[i].type==NUM)
{
BTnode* new=(BTnode*)malloc(sizeof(BTnode));
new->item=arr[i];
new->calnum=arr[i].uni.num;
new->left=new->right=NULL;
stack[top++]=new;
}
else
{
BTnode*new=(BTnode*)malloc(sizeof(BTnode));
top--;
BTnode* x1=stack[top];
top--;
BTnode* x2=stack[top];
new->left=x2;
new->right=x1;
if(arr[i].uni.ope=='+')
{
new->item=arr[i];
new->calnum=x1->calnum+x2->calnum;
}
else if(arr[i].uni.ope=='-')
{
new->item=arr[i];
new->calnum=x2->calnum-x1->calnum;
}
else if(arr[i].uni.ope=='*')
{
new->item=arr[i];
new->calnum=x2->calnum*x1->calnum;
}
else if(arr[i].uni.ope=='/')
{
new->item=arr[i];
new->calnum=x2->calnum/x1->calnum;
}
stack[top++]=new;
}
}
if(stack[0]->item.type==OP)
{
printf("%c ",stack[0]->item.uni.ope);
}
else if(stack[0]->item.type==NUM)
{
printf("%d ",stack[0]->calnum);
}
if(stack[0]->left)
{
if(stack[0]->left->item.type==OP)
{
printf("%c ",stack[0]->left->item.uni.ope);
}
else if(stack[0]->left->item.type==NUM)
{
printf("%d ",stack[0]->left->item.uni.num);
}
}
if(stack[0]->right)
{
if(stack[0]->right->item.type==OP)
{
printf("%c\n",stack[0]->right->item.uni.ope);
}
else if(stack[0]->right->item.type==NUM)
{
printf("%d\n",stack[0]->right->item.uni.num);
}
}
else
{
printf("\n");
}
printf("%d",stack[0]->calnum);
}
我在树结构体中加入了一项calnum,这一项是用于存储弹出的两个运算数运算后的值。如果遍历逆波兰表达式时,访问到运算数,那么calnum就等于运算数的值,如果是运算符,就存储弹栈出的两个数的值。
逆波兰表达式的转换我是直接copy上一次作业中写好的代码的,大家考试前也可以这么搞,就是把一些常用的算法结构写好,考试时候直接粘贴,考试浪费的时间 - -。
服务优化
【问题描述】
假设某机场所有**登机口(Gate)**呈树形排列(树的度为3),安检处为树的根,如下图所示。图中的分叉结点(编号大于等于100)表示分叉路口,登机口用小于100的编号表示(其一定是一个叶结点)。通过对机场所有出发航班的日志分析,得知每个登机口每天的平均发送旅客流量。作为提升机场服务水平的一个措施,在不改变所有航班相对关系的情况下(即:出发时间不变,原在同一登机口的航班不变),仅改变登机口(例如:将3号登机口改到5号登机口的位置),使得整体旅客到登机口的时间有所减少(即:从安检口到登机口所经过的分叉路口最少)。
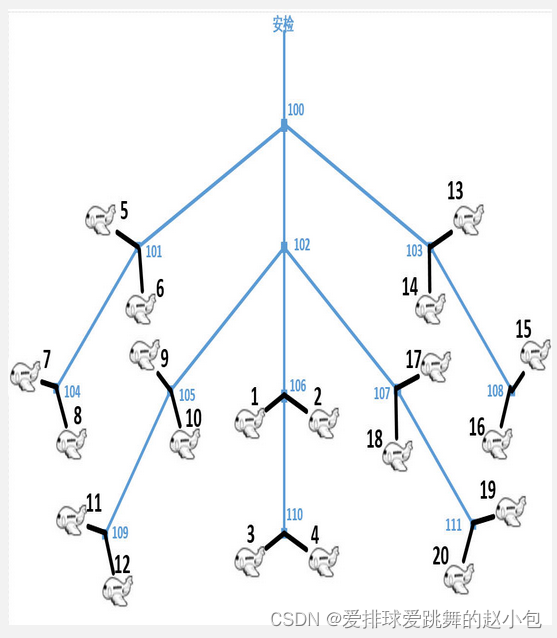
编写程序模拟上述登机口的调整,登机口调整规则如下:
1)首先按照由大到小的顺序对输入的登机口流量进行排序,流量相同的按照登机口编号由小到大排序;
2)从上述登机口树的树根开始,将登机口按照从上到下(安检口在最上方)、从左到右的顺序,依次对应上面排序后将要调整的登机口。
例如上图的树中,若只考虑登机口,则从上到下有三层,第一层从左到右的顺序为:5、6、14、13,第二层从左到右的顺序为:7、8、9、10、1、2、18、17、16、15,第三层从左到右的顺序为:11、12、3、4、20、19。若按规则1排序后流量由大至小的前五个登机口为3、12、16、20、15,则将流量最大的3号登机口调整到最上层且最左边的位置(即:5号登机口的位置),12号调整到6号,16号调整到14号,20号调整到13号,15号调整到第二层最左边的位置(即7号登机口的位置)。
【输入形式】
1)首先按层次从根开始依次输入树结点之间的关系。其中分叉结点编号从数字100开始(树根结点编号为100,其它分叉结点编号没有规律但不会重复),登机口为编号小于100的数字(编号没有规律但不会重复,其一定是一个叶结点)。树中结点间关系用下面方式描述:
R S1 S2 S3 -1
其中R为分叉结点,从左至右S1,S2,S3分别为树叉R的子结点,其可为树叉或登机口,由于树的度为3,S1,S2,S3中至多可以2个为空,最后该行以-1和换行符结束。各项间以一个空格分隔。如:
100 101 102 103 -1
表明编号100的树根有三个子叉,编号分别为101、102和103,又如:
104 7 8 -1
表明树叉104上有2个编号分别为7和8的登机口。
假设分叉结点数不超过100个。分叉结点输入的顺序不确定,但可以确定:输入某个分叉结点信息时,其父结点的信息已经输入。
输入完所有树结点关系后,在新的一行上输入-1表示树结点关系输入完毕。
2)接下来输入登机口的流量信息,每个登机口流量信息分占一行,分别包括登机口编号(1~99之间的整数)和流量(大于0的整数),两整数间以一个空格分隔。登机口数目与前面构造树时的登机机口数目一致。
【输出形式】
按照上述调整规则中排序后的顺序(即按旅客流量由大到小,流量相同的按照登机口编号由小到大)依次分行输出每个登机口的调整结果:先输出调整前的登机口编号,然后输出字符串"->"(由英文减号字符与英文大于字符组成),再输出要调整到的登机口编号。
【样例输入】
100 101 102 103 -1
103 14 108 13 -1
101 5 104 6 -1
104 7 8 -1
102 105 106 107 -1
106 1 110 2 -1
108 16 15 -1
107 18 111 17 -1
110 3 4 -1
105 9 109 10 -1
111 20 19 -1
109 11 12 -1
-1
17 865
5 668
20 3000
13 1020
11 980
8 2202
15 1897
6 1001
14 922
7 2178
19 2189
1 1267
12 3281
2 980
18 1020
10 980
3 1876
9 1197
16 980
4 576
【样例输出】
12->5
20->6
8->14
19->13
7->7
15->8
3->9
1->10
9->1
13->2
18->18
6->17
2->16
10->15
11->11
16->12
14->3
17->4
5->20
4->19
【样例说明】
样例输入了12条树结点关系,形成了如上图的树。然后输入了20个登机口的流量,将这20个登机口按照上述调整规则1排序后形成的顺序为:12、20、8、19、7、15、3、1、9、13、18、6、2、10、11、16、14、17、5、4。最后按该顺序将所有登机口按照上述调整规则2进行调整,输出调整结果。
【评分标准】
该题要求计算并输出登机口的调整方法,提交程序名为adjust.c。
咳咳来北航当程序员阅读能力一定要好……审题占写完整道题的50%……
首先,我们看看这个题的结构体怎么定义:树的度为三,那就是三叉树,我们应该在结构体里定义left mid right三个指针。
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#define MAX 100
typedef struct node
{
int id;
int passenger;
struct node* left;
struct node* mid;
struct node* right;
}BTNode;
BTNode* root;
int GateCount=0;
void Insert(int,BTNode*);
BTNode* findroot(int);
BTNode* find(int,BTNode*);
void Adjust(BTNode*);
int cmp1(const void* p1,const void* p2){
return (*(BTNode**)p2)->passenger-(*(BTNode**)p1)->passenger;
}
int cmp2(const void* p1,const void* p2){
return (*(BTNode**)p1)->id-(*(BTNode**)p2)->id;
}
int main()
{
int R,S;
scanf("%d",&R);
while(R!=-1)
{
BTNode* r=findroot(R);
scanf("%d",&S);
while(S!=-1)
{
if(S<100)
GateCount++;
Insert(S,r);
scanf("%d",&S);
}
scanf("%d",&R);
}
int gate,num;
for(int i=0;i<GateCount;i++)
{
scanf("%d %d",&gate,&num);
BTNode* Gate=find(gate,root);
Gate->passenger=num;
}
Adjust(root);
}
BTNode* find(int n,BTNode* p)
{
if(p==NULL)
return NULL;
if(p->id==n)
return p;
BTNode* tar=NULL;
tar=find(n,p->left);
if(tar==NULL)
tar=find(n,p->mid);
if(tar==NULL)
tar=find(n,p->right);
return tar;
}
BTNode* findroot(int r)
{
if(root==NULL)
{
root=(BTNode*)malloc(sizeof(BTNode));
root->id=r;
root->passenger=0;
root->left=root->right=root->mid=NULL;
return root;
}
return find(r,root);
}
void Insert(int s,BTNode* r)
{
BTNode* new=(BTNode*)malloc(sizeof(BTNode));
new->id=s;
new->passenger=0;
new->left=new->mid=new->right=NULL;
if(r->left==NULL)
{
r->left=new;
return;
}
if(r->left!=NULL&&r->mid==NULL)
{
r->mid=new;
return;
}
if(r->left!=NULL&r->mid!=NULL&&r->right==NULL)
{
r->right=new;
return;
}
}
void Adjust(BTNode* root)
{
BTNode* queue[MAX];
BTNode* Gates[GateCount];
int index=0;
int Front=0,Rear=MAX-1,Count=0;
Rear=(Rear+1)%MAX;
queue[Rear]=root;
Count++;
while(Count!=0)
{
BTNode* R=queue[Front];
Front=(Front+1)%MAX;
Count--;
if(R->left==NULL&&R->mid==NULL&&R->right==NULL)
Gates[index++]=R;
else
{
if(R->left)
{
Rear=(Rear+1)%MAX;
queue[Rear]=R->left;
Count++;
}
if(R->mid)
{
Rear=(Rear+1)%MAX;
queue[Rear]=R->mid;
Count++;
}
if(R->right)
{
Rear=(Rear+1)%MAX;
queue[Rear]=R->right;
Count++;
}
}
}
BTNode* Gates_1[GateCount];
memcpy(Gates_1,Gates,sizeof(BTNode*)*GateCount);
qsort(Gates_1,GateCount,sizeof(BTNode*),cmp1);
for(int i=0;i<GateCount;i++)
{
int num=1;
int start=i;
while(i+1<GateCount&&Gates_1[i]->passenger==Gates_1[i+1]->passenger)
{
i++;
num++;
}
if(num>1)
{
qsort(Gates_1+start,num,sizeof(BTNode*),cmp2);
}
}
for(int i=0;i<GateCount;i++)
{
printf("%d->%d\n",Gates_1[i]->id,Gates[i]->id);
}
}
这个题我觉得非常好,考点非常全面,考到了树的构造,树的遍历,查找指定节点,层序遍历,还有在快排中怎样以两个关键词排序。
最后还有一个小小的点需要注意一下:每个分支节点有三个指针,这三个指针可能都指向分支节点,也可能都指向登机口节点(图上没有表示,图上最多只有两个)。因此在插入树节点
词频统计(树实现)
【问题描述】
编写程序统计一个英文文本文件中每个单词的出现次数(词频统计),并将统计结果按单词字典序输出到屏幕上。
要求:程序应用二叉排序树(BST)来存储和统计读入的单词。
注:在此单词为仅由字母组成的字符序列。包含大写字母的单词应将大写字母转换为小写字母后统计。在生成二叉排序树不做平衡处理。
【输入形式】
打开当前目录下文件article.txt,从中读取英文单词进行词频统计。
【输出形式】
程序应首先输出二叉排序树中根节点、根节点的右节点及根节点的右节点的右节点上的单词(即root、root->right、root->right->right节点上的单词),单词中间有一个空格分隔,最后一个单词后没有空格,直接为回车(若单词个数不足三个,则按实际数目输出)。
程序将单词统计结果按单词字典序输出到屏幕上,每行输出一个单词及其出现次数,单词和其出现次数间由一个空格分隔,出现次数后无空格,直接为回车。
【样例输入】
当前目录下文件article.txt内容如下:
"Do not take to heart every thing you hear."she says.(这个she says是我自己加的)
“Do not spend all that you have.”
"Do not sleep as long as you want;"who(也是我加的)
【样例输出】
do not take
all 1
as 2
do 3
every 1
have 1
hear 1
heart 1
long 1
not 3
sleep 1
spend 1
take 1
that 1
thing 1
to 1
want 1
you 3
【样例说明】
程序首先在屏幕上输出程序中二叉排序树上根节点、根节点的右子节点及根节点的右子节点的右子节点上的单词,分别为do not take,然后按单词字典序依次输出单词及其出现次数。
【评分标准】
通过全部测试点得满分
为什么我要加一个she says呢?因为hear."she这一串中没有空格,如果你要用fscanf读的话,这个就被识别为一个单词了,但是很明显,这是两个独立的单词,hear和she,因此需要巧妙地处理一下:
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<ctype.h>
typedef struct node
{
char word[50];
int num;
struct node* left;
struct node* right;
}BTNode;
BTNode* root;
void Insert(char*);
void Inorder(BTNode*);
int main()
{
FILE* fp=fopen("article.txt","r");
//------------------------------------------------
//这部分用于单词的正确读写
int ch;
char str[50];
int index=0;
while((ch=fgetc(fp))!=EOF)
{
ch=tolower(ch);
if(ch>='a'&&ch<='z')
str[index++]=ch;
else
{
if(index>0)
{
str[index]='\0';
Insert(str);
index=0;
}
}
}
//这个判断很重要,
//因为如果最后一个单词后面没有标点,直接是EOF,
//那么最后一个单词就不正确插入树中,
//这也是为什么我在最后加了一个who的原因,用于测试这一部分。
if(index>0)
{
str[index]='\0';
Insert(str);
}
//-------------------------------------------------
if(root!=NULL)
{
printf("%s ",root->word);
}
if(root->right!=NULL)
{
printf("%s ",root->right->word);
}
if(root->right->right!=NULL)
{
printf("%s",root->right->right->word);
}
printf("\n");
Inorder(root);
return 0;
}
void Insert(char* s)
{
if(root==NULL)
{
root=(BTNode*)malloc(sizeof(BTNode));
strcpy(root->word,s);
root->num=1;
root->left=root->right=NULL;
return;
}
BTNode* cur=root;
while(1)
{
int cmp=strcmp(s,cur->word);
if(cmp==0)
{
cur->num++;
break;
}
else if(cmp>0)
{
if(cur->right==NULL)
{
BTNode* new=(BTNode*)malloc(sizeof(BTNode));
strcpy(new->word,s);
new->num=1;
new->left=new->right=NULL;
cur->right=new;
break;
}
else
cur=cur->right;
}
else
{
if(cur->left==NULL)
{
BTNode* new=(BTNode*)malloc(sizeof(BTNode));
strcpy(new->word,s);
new->num=1;
new->left=new->right=NULL;
cur->left=new;
break;
}
else
cur=cur->left;
}
}
}
void Inorder(BTNode* p)
{
if(p==NULL)
return;
Inorder(p->left);
printf("%s %d\n",p->word,p->num);
Inorder(p->right);
}