Understanding Diffusion Objectives as the ELBO with Simple Data Augmentation

引言

本文前作 VDM 已经推导出了扩散模型可以将优化 ELBO 作为目标函数。然而现在 FID （也就是感知质量）最好的模型还是用的其他目标函数（如 DDPM 的噪声预测和 Score-base Model 的得分匹配），本文证明了这些其他目标函数实际上也与 ELBO 相关。具体来说，本文证明了所有这些其他的扩散模型目标函数都可以写为 ELBO 在所有噪声等级上的加权积分，不同的目标函数决定了不同的加权函数。如果这个加权函数是单调的（许多扩散模型目标函数都满足这一点），本文进一步证明了不同的目标函数等价于 ELBO 目标搭配上简单的数据扩增（加性高斯噪声）。

方法

记真实数据分布为 $q(\mathbf{x})$ ，生成模型要做的事情是学习一个参数化分布 $p_{\theta }(\mathbf{x})$ 来近似 $q(\mathbf{x})$ ，以下简记 $p:=p_{\theta }$。

除了观测变量 $\mathbf{x}$，扩散模型中还有一系列隐变量 ${\mathbf{z}}_t,t\in [0,1]$ ，可记为 ${\mathbf{z}}_{0,\dots ,1}:={\mathbf{z}}_0,\dots ,{\mathbf{z}}_1$。扩散生成模型包含两部分：1）前向过程，表示为一个条件联合分布 $q({\mathbf{z}}_{0,\dots ,1}|\mathbf{x})$；2）参数化生成模型，表示为一个联合分布 $p({\mathbf{z}}_{0,\dots ,1})$。

前向过程和 noise schedule

前向过程是一个高斯扩散过程，表示为一个条件联合分布 $q({\mathbf{z}}_{0,...,1}|\mathbf{x})$。对于每个 $t\in [0,1]$，边缘分布 $q({\mathbf{z}}_t|\mathbf{x})$ 由以下公式给出：
$${\mathbf{z}}_t={\alpha }_{\lambda }\mathbf{x}+{\sigma }_{\lambda }ϵ,ϵ\sim \mathcal{N}(0,\mathbf{I})$$
可以看到，扩散模型前向过程的 “规格” 由 ${\alpha }_{\lambda },{\sigma }_{\lambda }$ 两组参数确定。如果是常用的 variance preserving 的前向过程，有 ${\alpha }_{\lambda }^2=\text{sigmoid}({\lambda }_t)$ 和 ${\sigma }_{\lambda }^2=\text{sigmoid}(-{\lambda }_t)$ 。但也有很多其他的扩散模型规格，本文的研究对于不同规格的扩散模型均成立。

定义时间步 $t$ 的对数信噪比（log signal to noise ratio, log SNR）为 $\lambda =\log ({\alpha }_t^2/{\sigma }_t^2)$ 。noise schedule $f_{\lambda }$ 是一个将时间步 $t\in [0,1]$ 映射为对应的 log SNR $\lambda$ 的函数，即有 $\lambda =f_{\lambda }(t)$。$f_{\lambda }$ 是严格单调递减的。log SNR $\lambda$ 是一个关于 $t$ 的函数，因此有时会将 log SNR 记为 ${\lambda }_t$。noise schedule 的两端点为 ${\lambda }_{\text{max}}:=f_{\lambda }(0)$ 和 ${\lambda }_{\text{min}}:=f_{\lambda }(1)$。由于$f_{\lambda }$ 的单调性，因此其也是可逆的，有 $t=f_{\lambda }^{-1}(\lambda )$。进一步基于这种双射，我们可以进行变量变换，一个关于 $t$ 的函数可以改写为关于 $\lambda$ 的函数，反之亦然。在接下来的研究中会用到这一点。

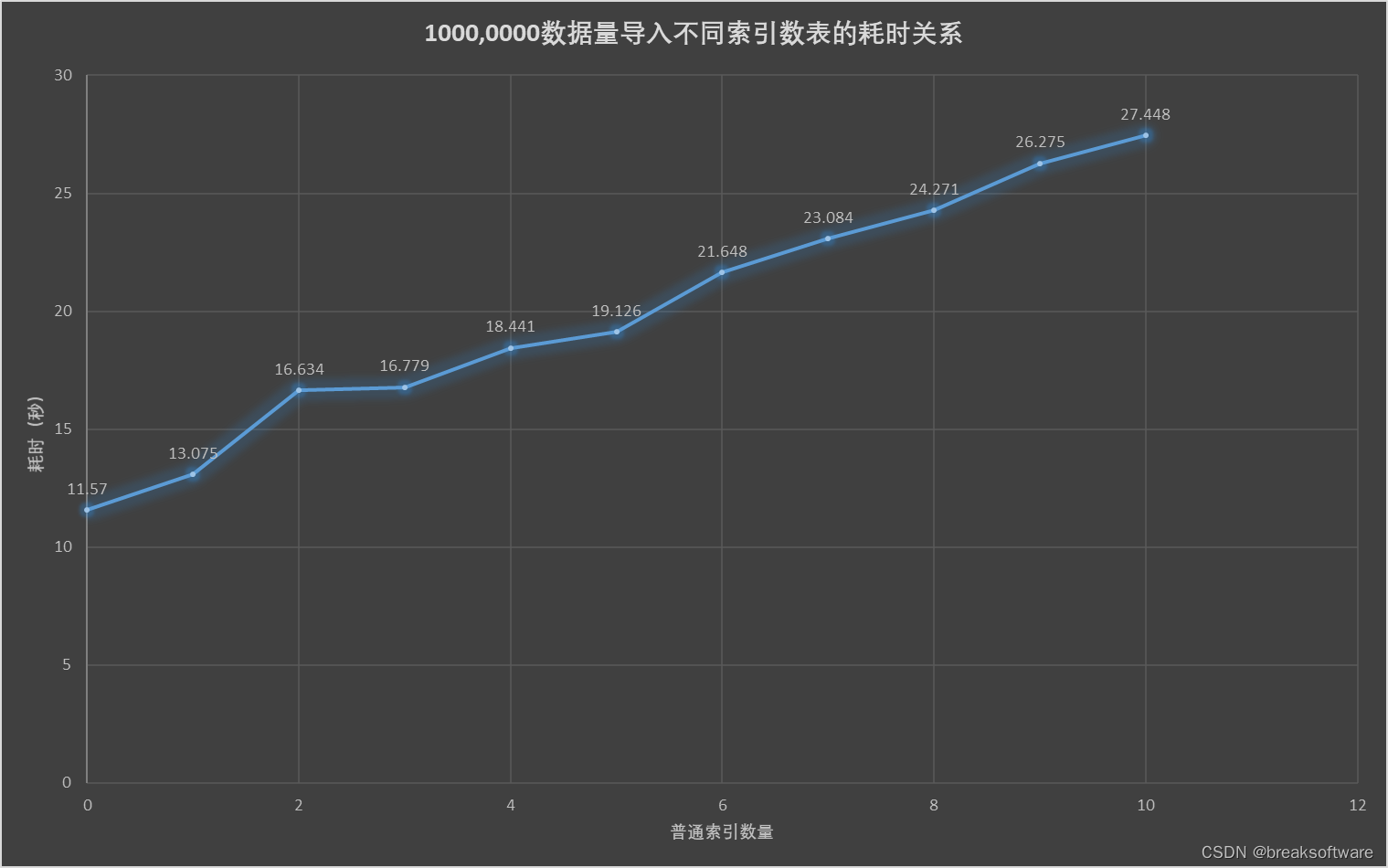
上图左侧展示了一些常见的 noise schedule。在训练阶段，我们均匀地采样时间 $t$ ：$t\sim \mathcal{U}(0,1)$ ，然后计算 $\lambda =f_{\lambda }(t)$ 。进一步可以推导出噪声等级的分布 $p(\lambda )=-dt/d\lambda =-1/f_{\lambda }^{\prime }(t)$ 。绘制在上图右侧。

有时在采样时使用与训练时不同的 noise schedule 会更好。在采样过程中，密度函数 $p(\lambda )$ 表示采样器在不同噪声水平上花费的相对时间量。

生成模型

真实数据 $\mathbf{x}\sim \mathcal{D}$ ，其分布密度为 $q(\mathbf{x})$ 。刚才介绍前向过程定义了一个联合分布 $q({\mathbf{z}}_0,\dots ,{\mathbf{z}}_1)=\int (q({\mathbf{z}}_{0,\dots ,1})|\mathbf{x}))d\mathbf{x}$ ，记边缘分布 $q_t(\mathbf{z})=q({\mathbf{z}}_t)$ 。生成模型则定义了一个对应的隐变量的联合分布 $p({\mathbf{z}}_0,\dots ,{\mathbf{z}}_1)$。

在扩散模型中，${\lambda }_{\text{max}}$ 足够大，${\mathbf{z}}_0$ 与数据 $\mathbf{x}$ 几乎相等，所以学习 $p({\mathbf{z}}_0)$ 等价于学习 $p(\mathbf{x})$ 。${\lambda }_{\text{min}}$ 足够小，${\mathbf{z}}_1$ 中几乎没有与 $\mathbf{x}$ 有关的信息，从而分布 $p({\mathbf{z}}_1)$ 满足 $D_{KL}(q({\mathbf{z}}_1|\mathbf{x})||p({\mathbf{z}}_1))\approx 0$ 。 因此一般有 $p({\mathbf{z}}_1)=\mathcal{N}(0,\mathbf{I})$。

记 ${\mathbf{s}}_{\theta }(\mathbf{z};\lambda )$ 为得分模型（score model），我们用该模型来估计得分 ${\nabla }_{\mathbf{z}}\log q_t(\mathbf{z})$ ，具体训练目标我们在下一节介绍。如果模型训练得足够好，可以完美完成估计任务，即有 ${\mathbf{s}}_{\theta }(\mathbf{z};\lambda )={\nabla }_{\mathbf{z}}\log q_t(\mathbf{z})$ ，那么生成模型就可以完全地反转（reverse）前向过程，生成新的数据。

如果有 $D_{KL}(q({\mathbf{z}}_1)||p({\mathbf{z}}_1))\approx 0$ 且 ${\mathbf{s}}_{\theta }(\mathbf{z};\lambda )\approx {\nabla }_{\mathbf{z}}\log q_t(\mathbf{z})$ ，我们就有一个好的生成模型能够做到 $D_{KL}(q({\mathbf{z}}_{0,\dots ,1})||p({\mathbf{z}}_{0,\dots ,1}))\approx 0$ ，从而就能实现我们的最终目标 ，拟合出真实数据分布，即 $D_{KL}(q({\mathbf{z}}_0)||p({\mathbf{z}}_0))\approx 0$ 。因此，我们生成式建模的任务就转换为学习一个网络 ${\mathbf{s}}_{\theta }(\mathbf{z};\lambda )$ 来拟合得分 ${\nabla }_{\mathbf{z}}\log q_t(\mathbf{z})$ 。

采样时，我们首先采样一个 ${\mathbf{z}}_1\sim p({\mathbf{z}}_1)$ ，然后使用估计的 ${\mathbf{s}}_{\theta }(\mathbf{z};\lambda )$ 来（近似）解反向 SDE。最近的扩散模型使用了越来越复杂的方法来解反向 SDE，本文实验中采用了 DDPM 的采样器和 Karras 等人提出的 Heun 二阶采样器。

不同的扩散模型训练目标

去噪得分匹配

Song 等人提出一种去噪得分匹配（denoising score matching）的方式来训练 ${\mathbf{s}}_{\theta }$ 估计得分 ${\nabla }_{\mathbf{z}}\log q_t(\mathbf{z})$ ：
$${\mathcal{L}}_{\text{DSM}}={\mathbb{E}}_{t\sim \mathcal{U}(0,1),ϵ\sim \mathcal{N}(0,\mathbf{I})}[\tilde{w}(t)\cdot ||{\mathbf{s}}_{\theta }({\mathbf{z}}_t;{\lambda }_t)-{\nabla }_{{\mathbf{z}}_t}\log q({\mathbf{z}}_t|\mathbf{x})|{|}_2^2]$$
其中 ${\mathbf{z}}_t={\alpha }_{\lambda }\mathbf{x}+{\sigma }_{\lambda }ϵ$ 。

$ϵ$-prediction 训练目标

大多数扩散模型的训练目标时 DDPM 中提出的噪声预测损失。这种情形下，得分模型一般被参数化为一个噪声预测（noise prediction，$ϵ$-prediction）网络：${\mathbf{s}}_{\theta }(\mathbf{z};\lambda )=-{\widehat{ϵ}}_{\theta }(\mathbf{z};\lambda )/{\sigma }_{\lambda }$ 。噪声预测损失可表示为：
$${\mathcal{L}}_{ϵ}(\mathbf{x})=\frac{1}{2}{\mathbb{E}}_{t\sim \mathcal{U}(0,1),ϵ\sim \mathcal{N}(0,\mathbf{I})}[||{\widehat{ϵ}}_{\theta }({\mathbf{z}}_t;{\lambda }_t)-ϵ|{|}_2^2]$$

由于有 $||{\mathbf{s}}_{\theta }({\mathbf{z}}_t;{\lambda }_t)-{\nabla }_{{\mathbf{z}}_t}\log q({\mathbf{z}}_t|\mathbf{x})|{|}_2^2={\sigma }_{\lambda }^{-2}||{\widehat{ϵ}}_{\theta }({\mathbf{z}}_t;{\lambda }_t)-ϵ|{|}_2^2$ ，所以这其实可以看作是去噪得分匹配目标函数在 $\tilde{w}(t)={\sigma }_{\lambda }^2$ 时的一种特殊情况。DDPM 中的实验结果显示，噪声预测这种目标函数训练出的模型可以产生非常高质量的生成结果，iDDPM 中将 noise schedule ${\lambda }_t$ 从线性换成了余弦，进一步提高了生成结果的质量。如今噪声预测损失+余弦 noise schedule 的扩散模型应用非常广泛。

与噪声预测目标 $ϵ$-prediction 类似的，还有 $\mathbf{x}$-prediction、$\mathbf{v}$-prediction、$\mathbf{o}$-prediction、$\mathbf{F}$-prediction 等形式。

ELBO 训练目标

本文前作 VDM 中提出了连续时间情形下的扩散模型的 ELBO 优化目标：
$$-\text{ELBO}(\mathbf{x})=\frac{1}{2}{\mathbb{E}}_{t\sim \mathcal{U}(0,1),ϵ\sim \mathcal{N}(0,\mathbf{I})}[-\frac{d\lambda }{dt}||{\widehat{ϵ}}_{\theta }({\mathbf{z}}_t;{\lambda }_t)-ϵ|{|}_2^2]+c$$
其中 $c$ 是与网络参数 $\theta$ 无关的常数。

加权损失

上述讨论的各种目标函数，其实都可以看作是 VDM 中的加权损失选择不同加权函数 $w({\lambda }_t)$ 的某种特殊情况。一般地，有：
$${\mathcal{L}}_w(\mathbf{x})=\frac{1}{2}{\mathbb{E}}_{t\sim \mathcal{U}(0,1),ϵ\sim \mathcal{N}(0,\mathbf{I})}[w({\lambda }_t)\cdot -\frac{d\lambda }{dt}||{\widehat{ϵ}}_{\theta }({\mathbf{z}}_t;{\lambda }_t)-ϵ|{|}_2^2]+c$$
显然 ELBO 目标是上式在未进行加权，即 $w({\lambda }_t)=1$ 时的情况；而噪声预测目标则是在 $w({\lambda }_t)=-dt/d\lambda$ 时的情况，或者更简洁地 $w({\lambda }_t)=p({\lambda }_t)$，训练时噪声水平 $\lambda$ 的隐含分布的 PDF。下面的图表展示了推导出的其他常用的扩散模型的隐式加权函数 $w(\lambda )$ 及其曲线。

加权损失关于 noise shedule 的不变性

VDM 中已经证明了 ELBO 目标函数关于 noise schedule （除开两端点 ${\lambda }_{\text{max}},{\lambda }_{\text{min}}$ 外）的不变性。这个结论在本文中进一步泛化到所有的加权扩散损失（上式）中。根据变量变换，将变量 $t$ 变换为 $\lambda$ ，有：
KaTeX parse error: Got function '\textcolor' with no arguments as subscript at position 44: …frac{1}{2}\int_\̲t̲e̲x̲t̲c̲o̲l̲o̲r̲{brown}{\lambda…
可以看到，上式这个积分（除了 ${\lambda }_{\text{max}},{\lambda }_{\text{min}}$ 之外）与 $f_{\lambda }$ （从 $t$ 到 $\lambda$ 的映射）无关。即，扩散损失不会受到 $f_{\lambda }$ 两端点 ${\lambda }_{\text{min}}$ 和 ${\lambda }_{\text{max}}$ 之间的函数形状的影响，而只会受到加权函数 $w(\lambda )$ 的影响。也就是说，给定一个加权函数 $w(\lambda )$ 之后，扩散损失是确定的，与 $t=0$ 和 $t=1$ 之间的 noise shedule ${\lambda }_t$ 无关的。从而我们有一个重要结论：不同扩散模型目标函数之间真正的区别，只在加权函数 $w(\lambda )$ 上。

当然，这种不变性对于训练时使用的，基于随机样本 $t\sim \mathcal{U}(0,1),ϵ\sim \mathcal{N}(0,\mathbf{I})$ 的蒙特卡洛估计器是不成立的。noise schedule 仍然会影响估计器的方差和梯度，从而会影响训练的效率。具体来说，noise schedule 可以看做是估计上述损失的一个重要性采样分布。结合 $p(\lambda )=-1(d\lambda /dt)$，我们可以将上式改写为：
$${\mathcal{L}}_w(\mathbf{x})=\frac{1}{2}{\mathbb{E}}_{\lambda \sim p(\lambda ),ϵ\sim \mathcal{N}(0,\mathbf{I})}[\frac{w(\lambda )}{p(\lambda )}||{\widehat{ϵ}}_{\theta }({\mathbf{z}}_{\lambda };\lambda )-ϵ|{|}_2^2]$$
从上式中可以清楚地看到 $p(\lambda )$ 作为重要性采样分布的角色。基于上述讨论的 noise schedule 特性，本文提出了一种自适应的 noise schedule，通过降低估计器的方差，有效提高了训练效率。

将加权损失看作是带数据扩增的 ELBO

结论：如果加权函数 $w({\lambda }_t)$ 是单调的，那么加权扩散目标函数等价于带数据扩增（加性高斯噪声）的 ELBO。

这里 $w({\lambda }_t)$ 是单调的，指的是其关于时间 $t$ 是单调递增的，从而其关于 $\lambda$ 是单调递减的。这在现如今很多扩散模型中都是成立的。

以下使用 ${\mathcal{L}}_{(}t,\mathbf{x})$ 来简记前向过程联合分布 $q({\mathbf{z}}_{0,\dots ,1}|\mathbf{x})$ 与反向过程对于时间步子集从 $t$ 到 1 下的生成模型 $p({\mathbf{z}}_{t,\dots ,1})$ 的 KL 散度，即：
$$\mathcal{L}(t,\mathbf{x}):=D_{KL}(q({\mathbf{z}}_{t,\dots ,1}|\mathbf{x})||p({\mathbf{z}}_{t,\dots ,1}))$$
可以证明，有：
$$\frac{d}{dt}\mathcal{L}(t;\mathbf{x})=\frac{1}{2}\frac{d\lambda }{dt}{\mathbb{E}}_{ϵ\sim \mathcal{N}(0,\mathbf{I})}[||ϵ-{ϵ}_{\theta }({\mathbf{z}}_{\lambda };\lambda )|{|}_2^2]$$

从而，可以将加权损失重写为：
$${\mathcal{L}}_w(\mathbf{x})=-{\int }_0^1\frac{d}{dt}\mathcal{L}(t;\mathbf{x})w({\lambda }_t)dt$$
再通过分部积分，可写为：
$${\mathcal{L}}_w(\mathbf{x})={\int }_0^1\frac{d}{dt}w({\lambda }_t)\mathcal{L}(t;\mathbf{x})+w({\lambda }_{\text{max}})\mathcal{L}(0;\mathbf{x})+\text{constant}$$
然后，由于我们假设 $w({\lambda }_t)$ 关于 $t\in [0,1]$ 是单调递增的。同时，不是一般性地，假设 $w({\lambda }_t)$ 以经过归一化，有 $w({\lambda }_1)=1$ 。我们可以进一步将加权损失简化为我们定义的 KL 散度的期望的形式：
$${\mathcal{L}}_w(\mathbf{x})={\mathbb{E}}_{p_w(t)}[\mathcal{L}(t;\mathbf{x})]+\text{constant}$$
其中 $p_w(t)$ 是由加权函数决定的一个概率分布，即 $p_w(t):=(d/dtw({\lambda }_t))$。在 $t\in [0,1]$ 上，分布 $p_w(t)$ 在 $t=0$ 处达到狄拉克函数峰值 $w({\lambda }_{\text{max}})$ ，该质量值一般非常小。

注意有：
$$\begin{array}{rl}\mathcal{L}(t;\mathbf{x})& =D_{KL}(q({\mathbf{z}}_{t\dots ,1}|\mathbf{x})||p({\mathbf{z}}_{t\dots ,1}))\\ & \ge D_{KL}(q({\mathbf{z}}_t|\mathbf{x})||p({\mathbf{z}}_t))\\ & ={\mathbb{E}}_{q({\mathbf{z}}_t|\mathbf{x})}[\log p({\mathbf{z}}_t)]+\text{constant}\end{array}$$
也就是说，$\mathcal{L}(t;\mathbf{x})$ 等于噪声扰动数据的负 ELBO 预期加上一个常数。至此，本节开头处的结论得证。

这个结论带给我们一个全新的理解视角：带（隐式）单调加权函数的训练目标，都可以等价于带简单的数据扩增（加性高斯噪声）的 ELBO 目标。这其实是一种形式的分布扩增（Distribution Augmentation, DistAug），其模型在训练时指定了对应的数据扩增条件，在采样时指定 “无扩增” 的条件。

加权函数对于感知质量的影响

对于扩散模型训练目标中的加权函数，也就是我们刚证明的单调加权函数下的带数据扩增的 ELBO，对于生成结果感知质量的影响，本节提出几个可能的解释。

与低比特训练的联系

Glow 中发现，移除 8bit 数据中最不重要的 3 个比特，使用 5bit 数据上，能训练处保真度更高的模型。一个可能的原因是，更关键的比特，对于人类的感知质量的影响也越大，移除不重要的 3 个比特能够使得模型更加聚焦于更重要的 5 个比特。Glow 中对低比特数据添加均匀噪声，然后送入模型，作者发现添加高斯噪声也有类似的作用。添加单一等级的高斯噪声，可以看作是加权损失在加权函数为阶跃函数时的一种特殊情况。均匀噪声的影响可以近似为一个经过 sigmoid 的加权函数。

傅里叶分析

为了更好地理解为什么加性高斯噪声能够提升生成图像的感知质量，我们从对一张带噪图片进行傅里叶变换（Fourier Transforme，FT）的角度来考虑。由于 FT 是一种线性变换，所以真实图像和高斯噪声的加和的 FT 等于二者各自高斯噪声的加和。自然图像的功率谱（即作为空间频率函数的 FT 平均幅度）会随着频率的增加而快速下降，这意味着最低频率的幅度最高。另一方面，高斯白噪声的功率谱大致恒定。当向干净的自然图像添加噪声时，高频区域的信噪比（即干净图像和高斯噪声图像的功率谱之比）会降低。因此，相比于低频信息，加性高斯噪声会更快地有效地破坏数据中的高频信息，从而迫使模型更多地关注数据的低频分量，而这些低频分量通常对应于对感知更为关键的高级内容和全局结构。

总结

VDM++ 在其前作 VDM 的基础上进一步在理论上分析了扩散模型中的 ELBO 目标。将得分匹配、噪声估计等训练目标通过不同的加权函数统一到 ELBO 目标中，并进一步掲示了当加权函数是单调函数时，不同的扩散模型训练目标相当于 ELBO 目标搭配上简单的数据扩增（加性高斯）。对后续许多扩散模型（如 SD3）的训练策略设计产生了重大影响。