【机器学习】【遗传算法】【项目实战】药品分拣的优化策略【附Python源码】

仅供学习、参考使用

一、遗传算法简介

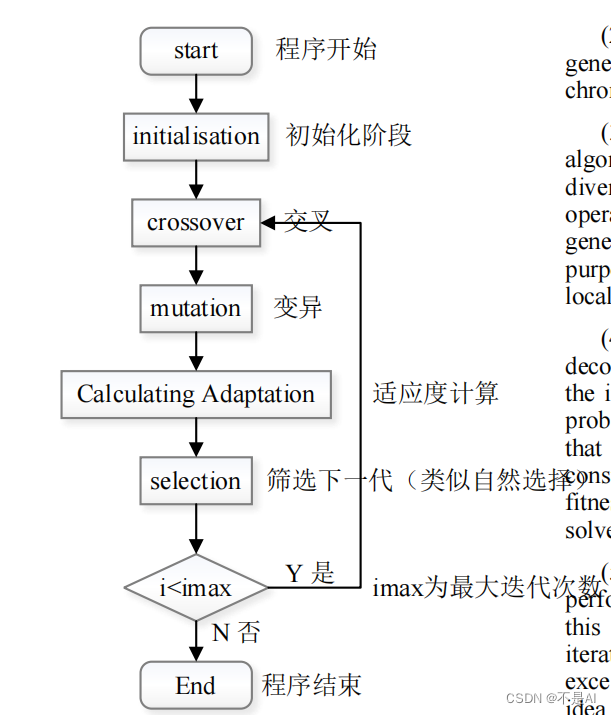
遗传算法（Genetic Algorithm, GA）是机器学习领域中常见的一类算法，其基本思想可以用下述流程图简要表示：

（图参考论文：Optimization of Worker Scheduling at Logistics
Depots Using GeneticAlgorithms and Simulated
Annealing）

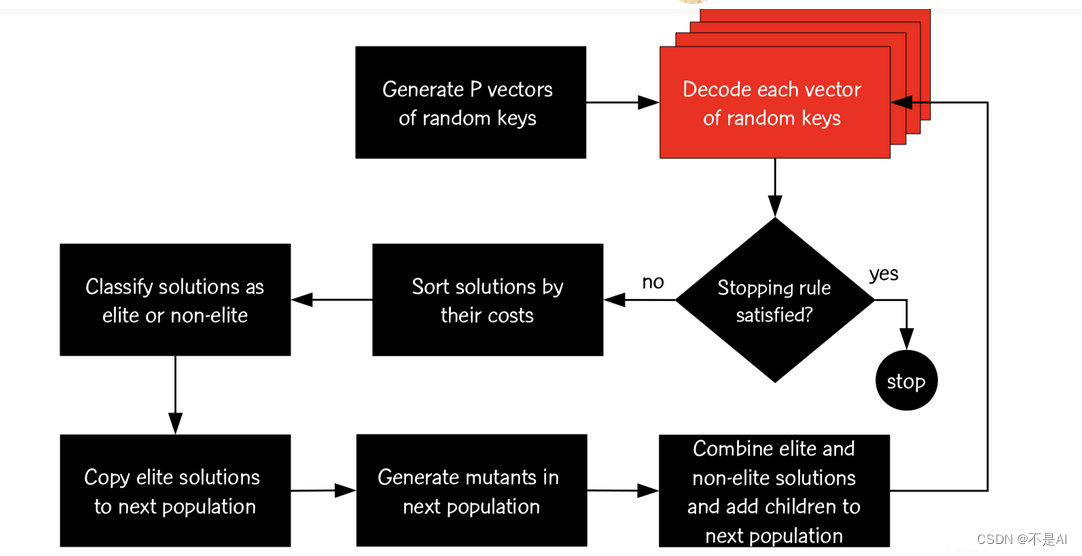
在这里插入图片描述

一种常见的遗传算法变例是有偏随机密匙遗传算法 (BRKGA: Biased Random Key Genetic Algorithm) ，参考论文：A BIASED RANDOM-KEY GENETIC ALGORITHM WITH VARIABLE MUTANTS TO
SOLVE A VEHICLE ROUTING PROBLEM，算法流程大致如下：
（图参考博客：Pymoo学习 (11)：有偏随机密匙遗传算法 (BRKGA: Biased Random Key Genetic Algorithm) 的使用）

在这里插入图片描述

二、项目源码（待进一步完善）

1、导入相关库

import csv
import random
import numpy as np
import pandas as pd
from datetime import datetime
import matplotlib.pyplot as plt

2、药品统计

# 统计zone_id=2110的药品
def screen_goods_id(tote_data, zone):
    zone_goods_id_lists = []
    for i in range(len(tote_data)):
        zone_id = tote_data['区段ID'][i]
        goods_id = tote_data['产品编号'][i]
        if zone_id == zone:
            zone_goods_id_lists.append(goods_id)
    zone_goods_id_lists = list(set(zone_goods_id_lists))
    return zone_goods_id_lists

3、货位统计

# 统计zone_id=2110的货位
def generate_locations():
    index_id_0 = [2173, 2174, 2175, 2176, 2177, 2178, 2179, 2180, 2181]
    index_id_1 = [1, 2, 3, 4, 5, 6, 7, 8]
    index_id_2 = [21, 22, 23, 24, 25, 31, 32, 33, 34, 35, 41, 42, 43, 44, 45]
    location_id_data = [f"{aa:04d}{bb:02d}{cc:02d}1" for aa in index_id_0 for bb in index_id_1 for cc in index_id_2]
    return location_id_data

4、缺失货位统计

# 统计zone_id=2110的缺失货位
def del_locations():
    index_id_0 = [217408, 217507, 217708, 217807, 218008, 218107]
    index_id_1 = [22, 23, 24, 25, 32, 33, 34, 35, 42, 43, 44, 45]
    del_loc_data = [f"{aa:06d}{bb:02d}1" for aa in index_id_0 for bb in index_id_1]
    return del_loc_data

5、生成可使用货位

# 去除缺失货位，生成最终的可使用货位
def screen_location_id():
    location_id_data = generate_locations()
    del_loc_data = del_locations()
    location_id_lists = [loc_id for loc_id in location_id_data if loc_id not in del_loc_data]
    return location_id_lists

6、个体（单个基因型）生成

# 生成一个个体
def pop_one_combined(list_1, list_2):  # list1的长度不能大于list2
    goods_ids_copy = list_1[:]
    location_ids_copy = list_2[:]
    combined_list = []
    for _ in range(len(list_1)):
        element = random.choice(location_ids_copy)
        location_ids_copy.remove(element)
        combined_list.append(element)
    return combined_list

生成测试：大小为6的一维数组，生成50个个体（种群类似）：

list1 = [1, 2, 3, 4, 5, 6]
list2 = [1, 2, 3, 4, 5, 6]

# 个体生成测试（批量生成）

for i in range(50):
    print(pop_one_combined(list1, list2))

在这里插入图片描述
7、种群（基因池）生成

# 生成种群
def generate_pop_list(POP_SIZE, zone_goods_id_data, zone_location_id_data):
    pop_list = []
    for _ in range(POP_SIZE):
        pop_individuality = pop_one_combined(zone_goods_id_data, zone_location_id_data)
        pop_list.append(pop_individuality)
    return pop_list

生成测试：

# 种群生成测试（样本量50）
print(generate_pop_list(50, list1, list2))

在这里插入图片描述
8、劳累值（特征系数）计算公式

# 拣选劳累值计算公式
def pick_distance_formula(location_id, shelves_num):
    if location_id[-2] == '4':  # 第4层（最高层）
        distance = 10 * (int(location_id[0:4]) - 2173) + (shelves_num - 1) * 10 + int(location_id[-3]) + 3
    else:  # 第1~3层
        distance = 10 * (int(location_id[0:4]) - 2173) + (shelves_num - 1) * 10 + int(location_id[-3])
    return distance

9、一组数据的劳累值计算

# 拣选劳累值计算(一组)
def pick_distance_value(location_id):
    distance = 0
    shelves_num = int(location_id[4:6])
    group_1 = [1, 3, 5, 7]
    group_2 = [2, 4, 6, 8]
    if shelves_num in group_1:
        shelves_num = shelves_num // 2 + 1
    elif shelves_num in group_2:
        shelves_num = shelves_num // 2
    distance = pick_distance_formula(location_id, shelves_num)
    return distance

10、选择优势个体进入下一代

# 选择优胜个体
def select(pop_list, CROSS_RATE, POP_SIZE):
    index = int(CROSS_RATE * POP_SIZE)  # 一轮筛选后的样本数量
    return pop_list[0:index]  # 返回前xxx个优胜个体

11、遗传变异机制

# 遗传变异
def mutation(MUTA_RATE, child, zone_goods_id_data, zone_location_id_data):
    if np.random.rand() < MUTA_RATE:
        mutation_list = [loc_id for loc_id in zone_location_id_data if loc_id not in child]
        num = np.random.randint(1, int(len(zone_goods_id_data) * MUTA_RATE))
        for _ in range(num):
            index = np.random.randint(0, len(zone_goods_id_data))
            mutation_list.append(child[index])
            loc_id = random.choice(mutation_list)
            child[index] = loc_id
    return child

12、子代中0值的替换

# （子代）0值的替换
def obx_count_run(child, parent):
    for parent_elemental in parent:
        if parent_elemental not in child:
            for i in range(len(child)):
                if child[i] == 0:
                    child[i] = parent_elemental
                    break
    return child

13、基于顺序的交叉方式（Order-Based Crossover, OBX）

# 遗传交叉（交叉算子：基于顺序的交叉（Order-Based Crossover，OBX））
def crossmuta(pop_list, POP_SIZE, MUTA_RATE, zone_goods_id_data, zone_location_id_data):
    pop_new = []
    for i in range(len(pop_list)):
        pop_new.append(pop_list[i][1:])
    while len(pop_new) < POP_SIZE:
        parent_1 = random.choice(pop_list)[1:]
        parent_2 = random.choice(pop_list)[1:]
        while parent_1 == parent_2:
            parent_2 = random.choice(pop_list)[1:]
        child_1 = [0 for _ in range(len(zone_goods_id_data))]
        child_2 = [0 for _ in range(len(zone_goods_id_data))]
        for j in range(len(zone_goods_id_data)):
            genetic_whether = np.random.choice([0, 1])
            if genetic_whether == 1:
                child_1[j] = parent_1[j]
                child_2[j] = parent_2[j]
        if (child_1 == parent_1) or (child_2 == parent_2):
            continue
        child_1 = obx_count_run(child_1, parent_2)
        child_1 = mutation(MUTA_RATE, child_1, zone_goods_id_data, zone_location_id_data)
        child_2 = obx_count_run(child_2, parent_1)
        child_2 = mutation(MUTA_RATE, child_2, zone_goods_id_data, zone_location_id_data)
        pop_new.append(child_1)
        pop_new.append(child_2)
    return pop_new

14、损失曲线图绘制

# 每轮总拣选劳累值绘制曲线图
def loss_chart(data):
    y_values = data
    x_values = list(range(len(y_values)))
    plt.plot(x_values, y_values)
    plt.title("zone_2110_pick_distance_loss")
    plt.xlabel("Iterations")  # 迭代次数
    plt.ylabel("zone_2110_pick_distance")  # 距离
    plt.grid()
    plt.savefig('./JS_zone_2110_pick_distance_loss.png')
    plt.show()

15、结果合成

# 最终结果合成
def goods_location_data_consolidation(zone_goods_id_data, zone_goods_location_id_data):
    goods_location_data = []
    for i in range(len(zone_goods_id_data)):
        goods_location_data.append([zone_goods_id_data[i], zone_goods_location_id_data[i]])
    return goods_location_data

主函数及运行：

def main():
    list1 = [1, 2, 3, 4, 5, 6]
    list2 = [1, 2, 3, 4, 5, 6]

    # 个体生成测试（批量生成）

    for i in range(50):
        print(pop_one_combined(list1, list2))

    # 种群生成测试（样本量50）
    print(generate_pop_list(50, list1, list2))

    print("Genetic algorithm run start")
    print(f"start_time --> {datetime.now()}")
    zone_2110_pick_distance = []
    tote_goods_data_2403 = pd.read_csv('./tote_goods_data_2024_03.csv')  # 读取数据集
    POP_SIZE = 20  # 种群大小
    CROSS_RATE = 0.9  # 交叉率
    MUTA_RATE = 0.05  # 变异率
    Iterations = 10  # 迭代次数
    zone_2110_goods_id_lists = screen_goods_id(tote_goods_data_2403, 2110)
    zone_2110_location_id_lists = screen_location_id()
    POP = generate_pop_list(POP_SIZE, zone_2110_goods_id_lists, zone_2110_location_id_lists)
    for i in range(Iterations):
        POP = getfitness(POP, 2110, tote_goods_data_2403, zone_2110_goods_id_lists)
        POP = select(POP, CROSS_RATE, POP_SIZE)
        zone_2110_pick_distance.append(POP[0][0])
        POP = crossmuta(POP, POP_SIZE, MUTA_RATE, zone_2110_goods_id_lists, zone_2110_location_id_lists)
    loss_chart(zone_2110_pick_distance)

    Updated_goods_location_data = goods_location_data_consolidation(zone_2110_goods_id_lists, POP[0])
    with open('./zone_2110_goods_location_data.csv', 'w', newline='') as csvfile:
        writer = csv.writer(csvfile)
        writer.writerow(['goods_id', 'location_id'])
        for row in Updated_goods_location_data:
            writer.writerow(row)

    print(f"end_time --> {datetime.now()}")
    print("Genetic algorithm run end")


if __name__ == "__main__":
    main()

三、算法测试

1、pop_size=20, iterations=10
cross_rate=0.5, muta_rate=0.05：
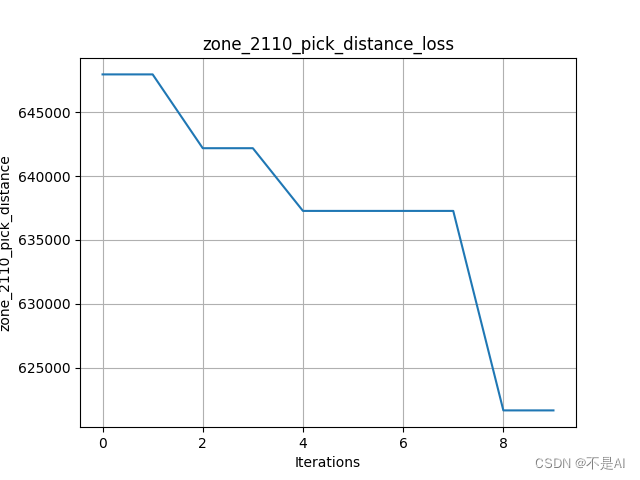
在这里插入图片描述
交叉率不变，增加变异率到0.1：

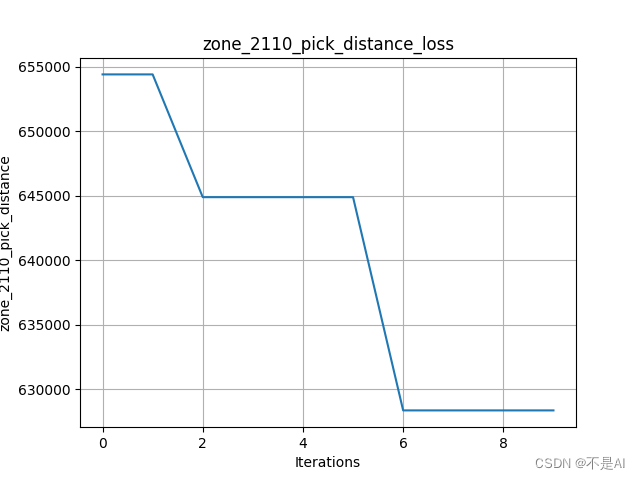
在这里插入图片描述

交叉率不变，增加变异率到0.2：

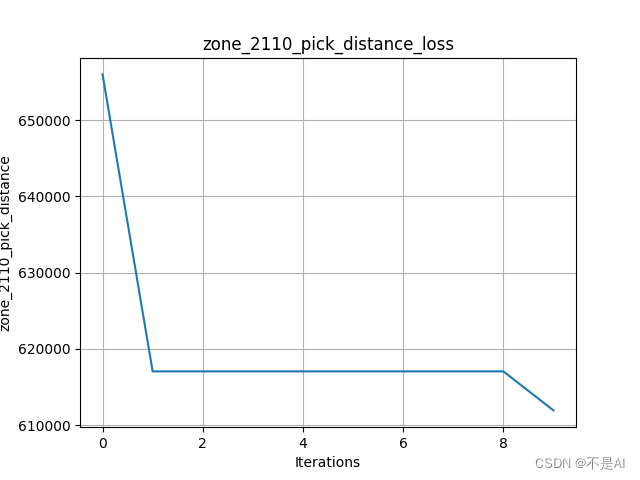
在这里插入图片描述

变异率不变，增加交叉率到0.9：

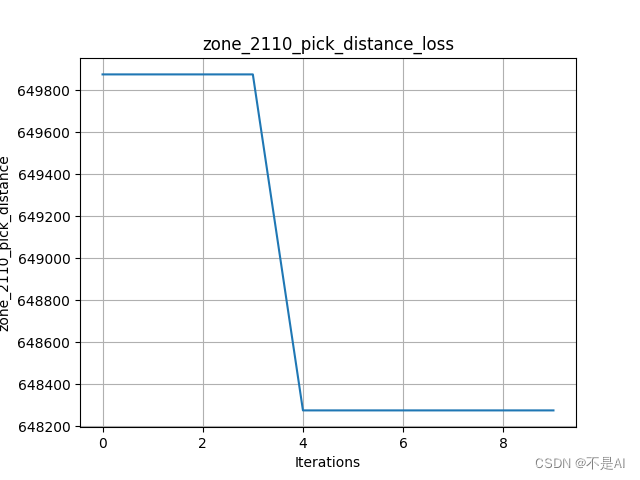
在这里插入图片描述

2、在另一个数据集上进行测试

采用初始参数设定：
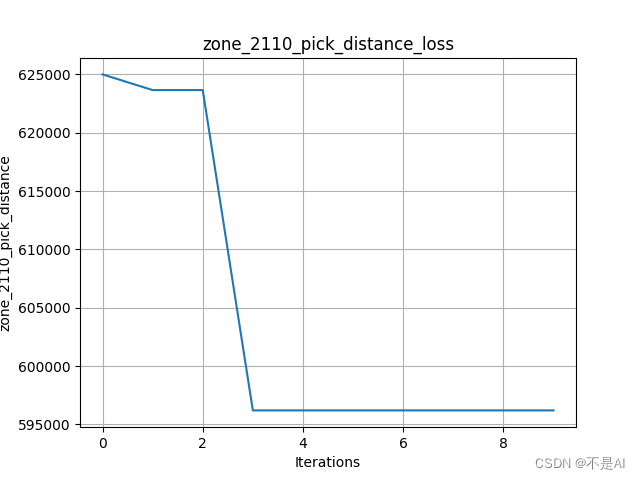
在这里插入图片描述

交叉率提高至0.9：
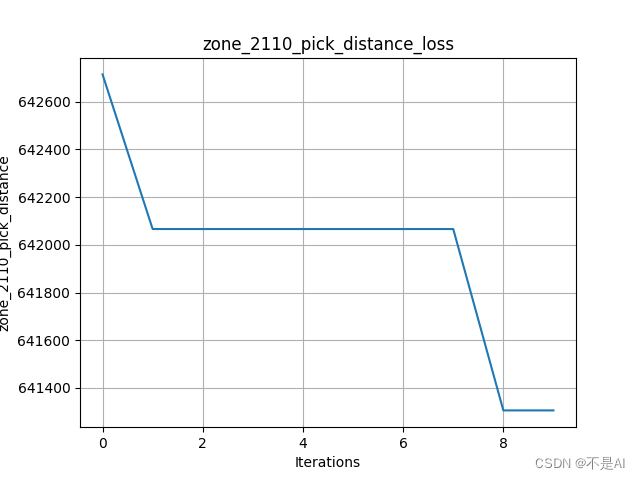
在这里插入图片描述

四、算法优化

GA（遗传）算法优化可行性分析

一、优化算法核心步骤参数

GA（Genetic Algorithm，遗传算法）的主要流程可以用下图进行简要描述：

在初始化阶段，需要确定imax（最大迭代次数）的值用于主循环的迭代。除这个值外，在算法的“交叉”步骤中，需要确定交叉方法（常用的交叉方法包括单点交叉、两点交叉、多点交叉、部分匹配交叉、均匀交叉、顺序交叉、基于位置的交叉、基于顺序的交叉、循环交叉、子路径交换交叉等），并指定参数cross_rate（交叉率）的值；在“变异”步骤中，需要指定参数muta_rate（变异率）的值；在“适应度计算”步骤中，需要自定义适应度（fitness）计算公式。故而可以进行优化的参数包括：
（1）最大迭代次数；
（2）交叉方法；（待验证）
（3）交叉率；
（4）变异率；（结论：提高变异率可以显著提高损失函数的收敛速度）
（5）适应度计算公式（涉及到按比例缩放的问题）。可能的策略：使用二次或者高次函数？如何提高损失函数的收敛速度？

二、采用GA的常见变式

上述流程图为GA的最基本的形式（基础GA），常见的优化变式包括：
（1）GA+SA——遗传算法结合模拟退火（Simulated Annealing）算法；
见论文：《Optimization of Worker Scheduling at Logistics
Depots Using Genetic Algorithms and Simulated
Annealing》
（2）AQDE（Adaptive Quantum Differential Evolution）算法（适应性量子差分进化算法）；
见论文：《Z. Sun, Z. Tian, X. Xie, Z. Sun, X. Zhang, and G. Gong, “An metacognitive based logistics human resource modeling and optimal
scheduling,”》
（3）BRKGA（Biased Random-Key Genetic Algorithm）算法（有偏随机密钥遗传算法）；
见论文：《A Biased Random-Key Genetic Algorithm With Variable Mutants To Solve a Vehicle Routing Problem》