【数据结构】十二、八种常用的排序算法讲解及代码分享

news2024/12/30 4:02:38

目录

一、插入排序

1)算法思想

2）代码

二、希尔排序

1）算法思想

2）代码

三、选择排序

1）算法思想

2）代码

四、堆排序

1）什么是最大堆

2）如何创建最大堆

3）算法思想

4）代码

五、冒泡排序

1）算法思想

2）代码

六、快速排序

1）算法思想

2）代码

七、归并排序

1）算法思想

2）代码

八、基数排序/桶排序（只对整数类型有效）

1）算法思想

2）代码

一、插入排序

1)算法思想

插入排序即将一个无序的元素集合中的元素一个个插入到子集合中合适的位置，直到原集合中的元素全部加入到子集合中。

2）代码

//插入排序
void Insert_Sort(DataType a[], int n)
{
    DataType temp;
    for (int i = 0; i < n - 1; i++)   //0 到 i 的数据已排序好
    {
        temp = a[i + 1];
        int j = i;
        while (j >= 0 && a[j] > temp) //如果是小于号则递增排序，如果是大于号则递减排序
        {
            a[j + 1] = a[j];
            j--;
        }
        a[j+1] = temp;
    }
}

二、希尔排序

1）算法思想

希尔排序算是插入排序的进阶版本，先把待排序的元素分为若干个小组，然后对每个小组进行插入排序。

这里的“增量（span）”代表将相邻span的元素分为一组，span的取值一般取n/2。

2）代码

//希尔排序
void Shell_Sort(DataType a[], int n)
{
    int span = n / 2;
    DataType temp;
    while (span > 0)
    {
        for (int i = 0; i < span; i ++)  //将数组分为span个小组
        {
            //对各组进行插入排序
            for (int k = i; k < n - span; k += span)
            {
                temp = a[k + span];
                int j = k;
                while (j >= 0 && a[j] > temp)
                {
                    a[j + span] = a[j];
                    j -= span;
                }
                a[j + span] = temp;
            }
        }
        span /= 2;
    }
}

三、选择排序

1）算法思想

每次从待排序的集合中选择最小（或最大）的元素放到集合的最前面，元素集合不断缩小，当待排序集合为空时代表排序结束。

2）代码

//选择排序
void Select_Sort(DataType a[], int n)
{
    DataType temp;
    for (int i = 0; i < n; i++)
    {
        DataType min = a[i];
        int k = i;
        for (int j = i; j < n; j++)
        {
            if (a[j] < min)
            {
                min = a[j];
                k = j;
            }
        }
        temp = a[i];
        a[i] = a[k];
        a[k] = temp;
    }
}

四、堆排序

1）什么是最大堆

1、完全二叉树结构；

2、双亲节点的值都比其孩子节点大。

2）如何创建最大堆

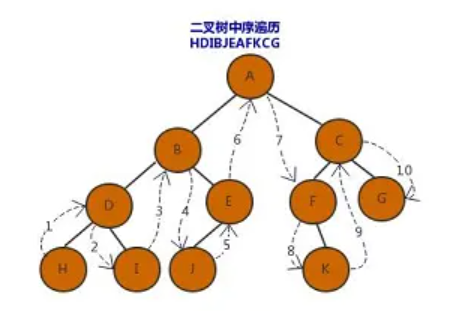
对于一个线性表，很容易可以将其转换为完全二叉树，因为线性表元素的下标是一一对应着完全二叉树的节点。我们先来记住两个重要的对应：

  1. （n-2）/ 2 ：表示最后一个非叶子节点；

  2.    2 * i + 1 ：表示第i个节点的左孩子；

将数组调整为大根堆的过程：

对应代码如下：

//其中n为数组a中的元素个数，h为要调整的元素的下标
static void CreatHeap(DataType a[], int n, int h)
{
    int flag = 0,i = h;
    DataType temp = a[i];
    int j = 2 * i + 1;   //先让j指向h左孩子节点的下标

    while (j < n && flag != 1)
    {
        //寻找左右孩子节点中的较大者，j为其下标
        if (j < n - 1 && a[j] < a[j + 1]) j++;    //第一个判断条件为该节点是否有右孩子，第二个判断条件为右孩子是否比左孩子大，若是，则j代表右节点的下标
        if (temp > a[j]) flag = 1;
        else {
            a[i] = a[j];          //将j位置的值上移，并且j更新为其左孩子节点的值
            i = j;
            j = 2 * i + 1;     
        }
    }
    a[i] = temp;
}

//创建大根堆
static void InitCreatHeap(DataType a[], int n)
{
    for (int i = (n - 2) / 2; i >= 0; i--)            //(n-2)/2表示左后一个非叶子节点的下标
        CreatHeap(a, n, i);
}

3）算法思想

通过第二部分的操作，我们已经成功地把数组转换为了大根堆，接下来只需要不断将根节点元素与数组末尾元素进行交换，再更新大根堆即可。

为什么不从最后面的叶子节点开始拿？因为我们无法保证最后一个元素一定是最小的！

例如：（a）将88和5进行交换，随后为保持为大根堆，5与76交换，再与50交换，得到（b）。

4）代码

void Heap_Sort(DataType a[], int n)
{
    DataType temp;
    InitCreatHeap(a, n);    //先初始化整个数组为大根堆
    for (int i = n - 1; i > 0; i--)    //不断将根节点元素放与数组末尾元素进行交换
    {
        temp = a[0];
        a[0] = a[i];
        a[i] = temp;
        CreatHeap(a, i, 0);
    }
}

五、冒泡排序

1）算法思想

冒泡排序是从第一个元素开始，将相邻的元素两个两个进行比较，每趟比较都将集合中最大（或最小）的元素放到了集合末尾。

2）代码

//冒泡排序
void Bubble_Sort(DataType a[], int n)
{
    DataType temp;
    int flag = 1;            //判断是否提前排序完成
    for (int i = n; i > 0 && flag; i--)
    {
        flag = 0;
        for (int j = 0; j < i-1; j++)
        {
            if (a[j] > a[j + 1])
            {
                temp = a[j];
                a[j] = a[j + 1];
                a[j + 1] = temp;
                flag = 1;                //仍然有元素进行交换，排序未完成
            }
        }
    }
}

六、快速排序

1）算法思想

快速排序定义了一个数组的下界low和上界high，然后通过两端的指针不断与low处的元素进行比较，将比low处的元素小的元素放到左边，将所有比他大的元素放到右边，这样一来，该元素的左边的元素都比他小，右边的元素都比他大，然后递归对左边和右边的集合进行快速排序即可。

2）代码

//快速排序
static void QuickSort(DataType a[], int low,int high)
{
    int i = low, j = high;
    DataType temp = a[low];

    while (i < j) {
        while (i < j && temp <= a[j])j--;
        if (i < j) {
            a[i] = a[j];
            i++;
        }

        while (i < j && temp >= a[i])i++;
        if (i < j) {
            a[j] = a[i];
            j--;
        }
    }

    a[i] = temp;
    if(i>low) QuickSort(a, low, i - 1);
    if(j<high) QuickSort(a, j + 1, high);
}

诶！🧐这个排序有点不一样，前面的排序参数都是数组和元素个数，但是它居然有三个参数！逼死强迫症！为了使用时方便统一，我们封装一下：

//快速排序
void Quick_Sort(DataType a[], int n)
{
    QuickSort(a, 0, n - 1);   //注意上界和下界都是可取的
}

七、归并排序

1）算法思想

将具有n个元素的数组a看成n个长度为1的有序子数组，然后从第一个子数组开始，把相邻的两个子数组两两合并，然后再将合并后的数组两两合并，直到只剩下最后一个数组。

2）代码

//一次二路归并算法
static void Merge(DataType a[], int n, DataType swap[], int k)
{
    //k为有序子数组的长度，一次二路归并排序后的有序子数列存于swap
    int lower1 = 0;   //第一个有序子序列的下界
    int lower2, upper1, upper2,m = 0,i,j;
    while (lower1 + k <= n - 1) {
        lower2 = lower1 + k;       //第二个有序子数组的下界
        upper1 = lower2 - 1;       //第一个有序子数组的上界
        upper2 = (lower2 + k - 1 <= n - 1) ? lower2 + k - 1 : n - 1;//第二个有序子数组的上界

        //合并两个有序子数组
        for (i = lower1,j = lower2; i <= upper1 && j <= upper2; m++) {
            if (a[i] < a[j]) {
                swap[m] = a[i++];
            }
            else swap[m] = a[j++];
        }

        //如果子数组2已存完，则把数组1中剩余的元素存入swap
        while (i <= upper1) swap[m++] = a[i++];

        //如果子数组1已存完，则把数组2中剩余的元素存入swap
        while (j <= upper2) swap[m++] = a[j++];

        lower1 = upper2 + 1;
    }
    //如果原数组不能构成两组子数组，则直接存入swap
    for (int i = lower1; i < n; i++, m++)
        swap[m] = a[i];
}

//二路归并排序
void Merge_Sort(DataType a[], int n)
{
    DataType* swap = (DataType*)malloc(sizeof(DataType) * n);
    int k = 1;
    while (k < n)
    {
        Merge(a, n, swap, k);
        for (int i = 0; i < n; i++)
            a[i] = swap[i];
        k *= 2;
    }
    free(swap);
}

八、基数排序/桶排序（只对整数类型有效）

1）算法思想

设待排序的元素是m位的d进制的数，不足m位的在高位补0，设置d个桶（实际上是队列），其编号为0、1、2…d-1。首先按照元素的低位的数组依次把各元素放入相应编号的队列中，然后从小到大的编号依次出队列，放回到原数组，这样就完成了一轮排序。接着按高一位的数值再次放入桶中，再出队列，直到进行m轮排列，数组中的元素就有序了。

2）代码

这里我们使用链式队列。

//桶排序
//针对整数类型
void Radix_Sort(DataType a[], int n, int m, int d)  //m位的d进制数
{
    int k, power = 1;
    QueuePtr* tub = (QueuePtr*)malloc(sizeof(QueuePtr) * d);
    if (tub == NULL)
    {
        printf("内存分配失败！\n");
        return;
    }
    for (int i = 0; i < d; i++) {
        LinkQueue_Init(&tub[i]);
    }

    //进行m次存放
    for (int i = 0; i < m; i++) {
        if (i == 0)power = 1;
        else power *= d;

        //将元素按关键字第k位的数值放入相应队列
        for (int j = 0; j < n; j++) {
            k = a[j] / power - (a[j] / (power * d)) * d;
            LinkQueue_Add(&tub[k], a[j]);
        }

        //顺序回收各队列中的元素至数值a中
        k = 0;
        for (int j = 0; j < n; j++) {
            while (!LinkQueue_Empty(tub[j])) {
                a[k++] = LinkQueue_Pop(&tub[j]);
            }
        }
    }
}

以上就是今天分享的全部内容，最后感谢你观看完我的文章，如果文章对你有帮助，可以点赞收藏评论，这是对作者最好的鼓励！不胜感激🥰

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1806267.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Databricks Data Warehouse

Databricks Data Warehouse

Warehouse features 原来的data warehouse痛点&#xff1a; 用例不兼容的支持模型的安全和管理不兼容不相交和重复的数据 ETL workloads Streaming Architecture Data Science and ML
阅读更多...
演讲全文｜林涛：MongoDB助力智能制造出海控本增效

演讲全文｜林涛：MongoDB助力智能制造出海控本增效

5月29日-30日在上海世博中心举办的亚马逊云科技中国峰会圆满结束。本文整理了MongoDB北亚区方案与咨询总监林涛在白金讲堂的演讲全文&#xff0c;就《MongoDB助力智能制造出海控本增效》话题与大家共同探讨。 白金讲堂演讲视频 从全球经济竞争的角度看&#xff0c;中国制造业…
阅读更多...
原来你长这个样子啊，Java字节码文件

原来你长这个样子啊，Java字节码文件

字节码文件 字节码文件是一种二进制文件&#xff0c;扩展名为.class 通过 javac 将源码编译得到&#xff0c;是一种中间形式的代码&#xff0c;这种中间形式的代码让Java有了“一次编译&#xff0c;多次运行”的跨平台特点。 字节码文件的组成 由5大组成部分&#xff1a;基础…
阅读更多...
【SQLAlChemy】如何连接数据库？

【SQLAlChemy】如何连接数据库？

使用SQLAlChemy连接数据库 导入包 首先&#xff0c;导入创建数据库引擎的包。 from sqlalchemy import create_engine编写数据库配置 SQLALCHEMY_DATABASE_URL "mysql://root:123456789127.0.0.1:3306/tortoise"字段解释&#xff1a; mysql:&#xff1a;这是数…
阅读更多...
Python第二语言（七、Python模块）

Python第二语言（七、Python模块）

目录 1. 什么是模块 2. 基本语法 2.1 模块的导入方式 2.2 基本语法 import 模块名 2.3 基本语法 from 模块名 import 功能名 2.4 基本语法as 别名 3. 自定义模块 4. 调用自定义模块时&#xff0c;如何让其模块中的函数不被调用&#xff08;__name__&#xff09; 5. 调…
阅读更多...
fl studio怎么设置中文及 2024年最新fl studio选购指南

fl studio怎么设置中文及 2024年最新fl studio选购指南

FL Studio让你的计算机就像是全功能的录音室&#xff0c;漂亮的大混音盘&#xff0c;先进的创作工具&#xff0c;让你的音乐突破想象力的限制。zol提供FL Studio中文版下载。 FL Studio中文版下载软件简介 FL Studio 让你的计算机就像是全功能的录音室&#xff0c;漂亮的大混…
阅读更多...
Linux的网络配置

Linux的网络配置

查看网络配置命令 一、查看所有活动的网络接口信息 ifconfig ifconfig 展示的是当前设备正在工作的网卡&#xff08;启动的设备&#xff09; ifconfig -a 展示所有的网络设备 ifconfig ens33 查看指定网卡设备 ifconfig ens33 down 关闭网卡 或者 ifdown ens33 &#xff0…
阅读更多...
论文阅读KAN: Kolmogorov–Arnold Networks

论文阅读KAN: Kolmogorov–Arnold Networks

学习了最近大热的KAN网络 论文地址&#xff1a;https://arxiv.org/pdf/2404.19756 按我个人读论文的习惯总结了如下几点&#xff1a; 1&#xff0c;背景&#xff1a; 1&#xff09;灵感来源&#xff1a;于Kolmogorov-Arnold表示定理&#xff0c;也就是多变量连续函数可以表…
阅读更多...
大模型常用推理参数工作原理

大模型常用推理参数工作原理

&#x1f34e;个人主页&#xff1a;小嗷犬的个人主页 &#x1f34a;个人网站&#xff1a;小嗷犬的技术小站 &#x1f96d;个人信条&#xff1a;为天地立心&#xff0c;为生民立命&#xff0c;为往圣继绝学&#xff0c;为万世开太平。 do_sample do_sample 参数控制是否使用采样…
阅读更多...
戴尔R720服务器(3)组RAID

戴尔R720服务器(3)组RAID

今天收到7块硬盘&#xff0c;现在共有8块硬盘了&#xff0c;找了个视频学习了怎么使用阵列卡组RAID并记录。 ​​ ‍ 视频参考&#xff1a;【戴尔服务器添加RAID5热备盘hotspare】 ‍ 阵列卡组RAID5 开始 连接iDRAC控制台服务器开机按F2进入BIOS选择Device Settings​ ​​…
阅读更多...
知识图谱的应用---智能电网

知识图谱的应用---智能电网

文章目录 智能电网典型应用 智能电网 智能电网以物理电网为基础&#xff0c;将现代先进的传感测量技术、通讯技术、信息技术、计算机技术和控制技术与物理电网高度集成而形成的新型电网。它以充分满足用户对电力的需求和优化资源配置、确保电力供应的安全性、可靠性和经济性、满…
阅读更多...
C++输入输出与IO流

C++输入输出与IO流

C 输入输出与I/O流 文章目录 C 输入输出与I/O流IO类型与基础特性概念与特性IO状态输出缓冲区 文件输入输出文件模式 string流IO处理中常用的函数及操作符综合练习与demo一、 创建文件并写入二、控制台输入数据并拆分存储三、读写电话簿 IO类型与基础特性 C11标准提供了几种IO处…
阅读更多...
【ArcGIS微课1000例】0117：ArcGIS中如何将kml（kmz）文件转json（geojson）？

【ArcGIS微课1000例】0117：ArcGIS中如何将kml（kmz）文件转json（geojson）？

文章目录 一、kml获取方式二、kml转图层三、图层转json一、kml获取方式 kml文件是一种很常用的数据格式，可以从谷歌地球（googleearth）获取某一个地区的kml范围文件，如青海湖（做好的kml文件可以从配套实验数据包0117.rar中获取）。 二、kml转图层 打开【KML转图层】工具，…
阅读更多...
前端项目打包、部署的基础 (vue)

前端项目打包、部署的基础 (vue)

详细请看B站视频 BV19n4y1d7Gr 《禹神&#xff1a;前端项目部署指南&#xff0c;前端项目打包上线》&#xff0c;本博客为自用视频笔记。 目录 项目打包vue打包打包前分析项目请求 本地服务器部署问题 & 解决问题1&#xff1a;刷新页面404问题问题2&#xff1a;ajax请求废…
阅读更多...
最新下载：PDFFactoryFinePrint【软件附加安装教程】

最新下载：PDFFactoryFinePrint【软件附加安装教程】

简介&#xff1a; pdfFactory是一款无须 Acrobat 创建 Adobe pdf 文件的打印机驱动程序&#xff0c; 提供的创建 PDF 文件的方法比其他方法更方便和高效。 pdfFactory 支持从所有应用程序轻松、可靠地创建 PDF 文件。 支持将单页或两页的文档&#xff0c;直接打印为PDF文件&a…
阅读更多...
信息学奥赛初赛天天练-24-二叉树、N叉树遍历技巧与前缀表达式、中缀表达式、后缀表达式应用实战演练

信息学奥赛初赛天天练-24-二叉树、N叉树遍历技巧与前缀表达式、中缀表达式、后缀表达式应用实战演练

PDF文档公众号回复关键字:20240609 单项选择题（共15题，每题2分，共计30分：每题有且仅有一个正确选项） 5 根节点的高度为1，一根拥有2023个节点的三叉树高度至少为（ ）。 A 6 B 7 C 8 D 9 8 后缀表达式 6 2 3 + - 3 8 2 / + * 2 ^ 3 + 对应的中缀表达式是（ ） A ((…
阅读更多...
[Linux]内网穿透nps

[Linux]内网穿透nps

文章目录 基础文件下载项目地址下载地址 客户端安装解压文件客户端启动客户端注册到linux系统服务客户端注册到windows系统服务windows bat 一键管理员注册windows bat 一键管理员取消 基础文件下载 项目地址 https://github.com/ehang-io/nps 下载地址 Releases ehang-io…
阅读更多...
12.打渔还是晒网

12.打渔还是晒网

上海市计算机学会竞赛平台 | YACSYACS 是由上海市计算机学会于2019年发起的活动，旨在激发青少年对学习人工智能与算法设计的热情与兴趣，提升青少年科学素养，引导青少年投身创新发现和科研实践活动。https://www.iai.sh.cn/problem/17 题目描述 有句俗话叫“三天打渔，两天…
阅读更多...
VBA高级应用30例应用2实现在列表框内及列表框间实现数据拖动

VBA高级应用30例应用2实现在列表框内及列表框间实现数据拖动

《VBA高级应用30例》&#xff08;版权10178985&#xff09;&#xff0c;是我推出的第十套教程&#xff0c;教程是专门针对高级学员在学习VBA过程中提高路途上的案例展开&#xff0c;这套教程案例与理论结合&#xff0c;紧贴“实战”&#xff0c;并做“战术总结”&#xff0c;以…
阅读更多...
AI大模型学习（非常详细）零基础入门到精通，收藏这一篇就够了

AI大模型学习（非常详细）零基础入门到精通，收藏这一篇就够了

前言 随着人工智能技术的快速发展&#xff0c;AI大模型学习正成为一项备受关注的研究领域。为了提高模型的准确性和效率&#xff0c;研究者们需要具备深厚的数学基础和编程能力&#xff0c;并对特定领域的业务场景有深入的了解。通过不断优化模型结构和算法&#xff0c;AI大模…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023