排序-读取数据流并实时返回中位数

news2025/1/11 0:23:05

一、问题描述

二、解题思路

1.顺序表排序法

2.使用大根堆、小根堆

三、代码实现

1.顺序表排序法实现

2.大根堆、小根堆法实现

四、刷题链接

一、问题描述

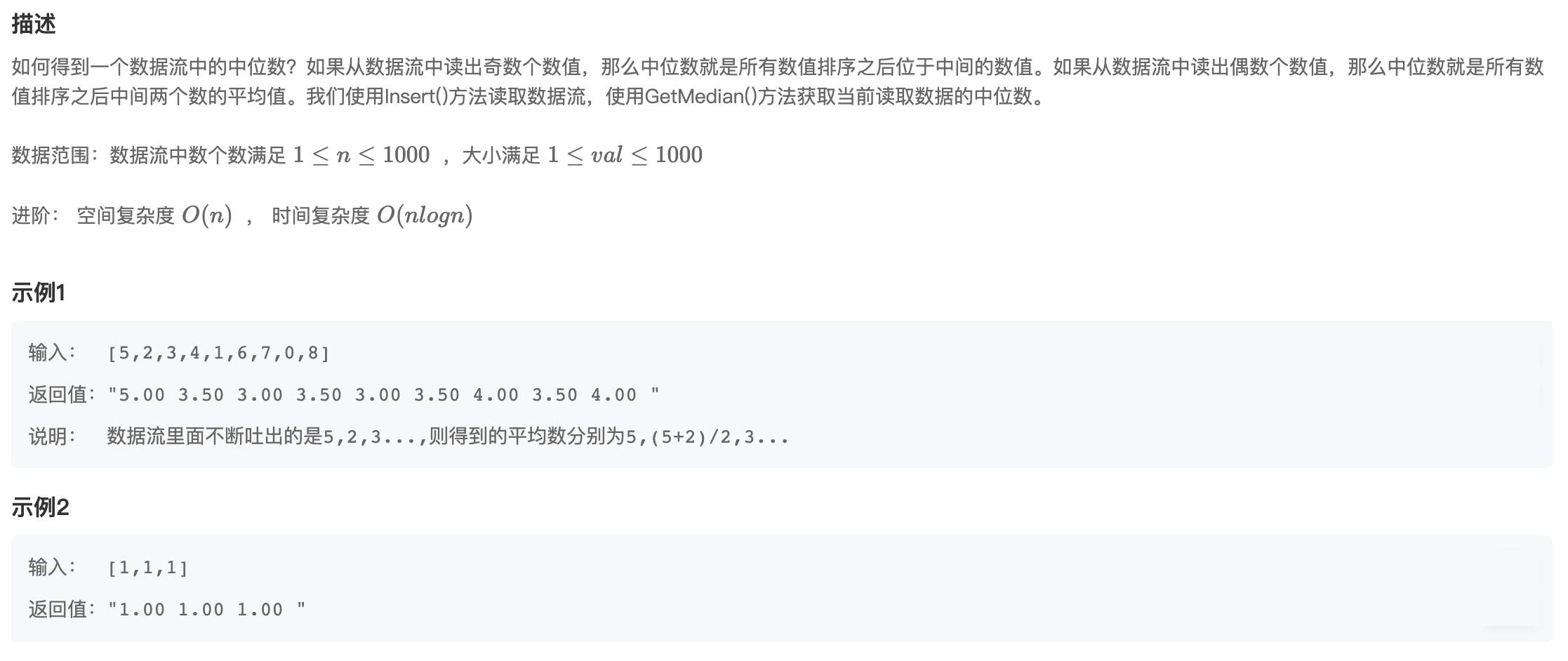
二、解题思路

1.顺序表排序法

（1）每次读取一个数就对列表排一次序，对排序过后的列表找中位数

（2）找中位数时注意顺序表长度，如果为奇数则找中间元素直接返回，如果是偶数，需要找中间两个元素求平均数作为中位数返回。

这种方法效率较低，下面提供一种效率高的方法，利用了堆调整速度快的特点，提高效率。

2.使用大根堆、小根堆

小根堆里放较大的一半元素，大根堆放较小的一半元素，之所以这样放，我们举个例子说明一下。

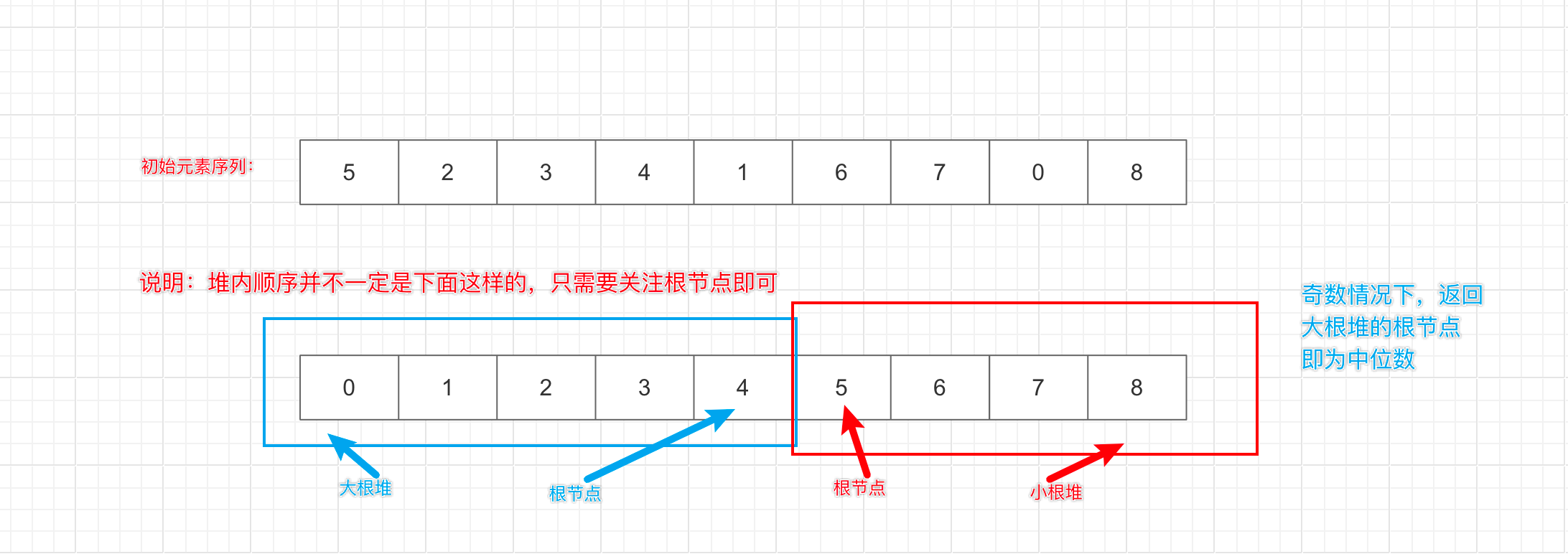
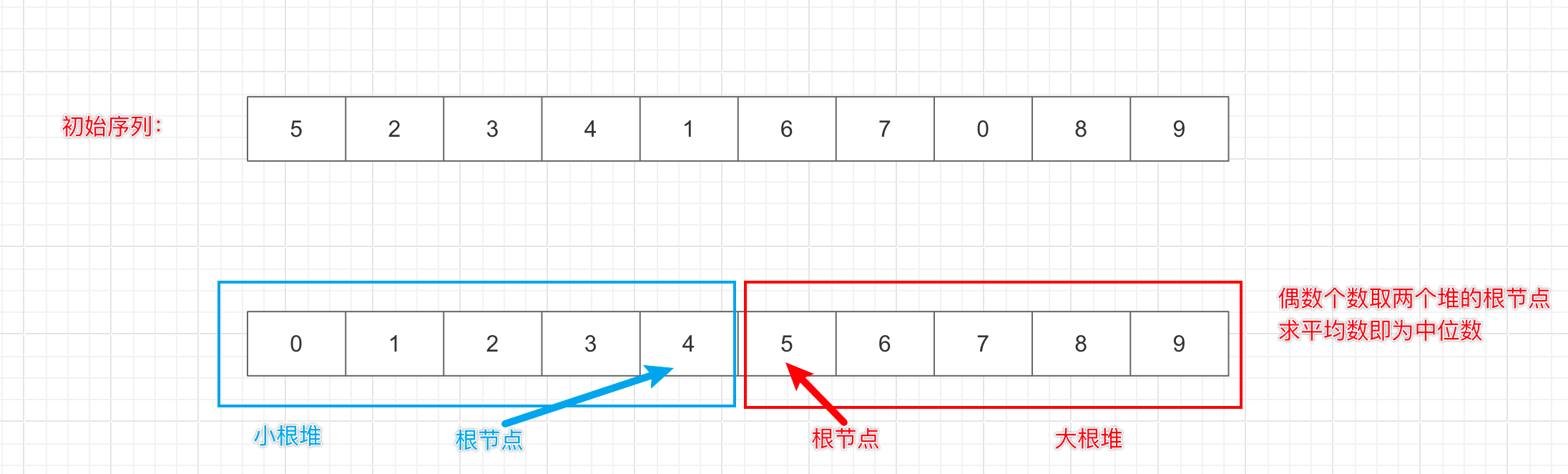
注意：保持 0=<小根堆元素数量-大根堆元素数量<=1

新加入元素的调整流程：新读取的元素并不一定是序列中较大的一半，新读取元素放入小根堆中，此时小根堆调整，根节点是小根堆中最小的元素（是序列中较小一半的元素），放入大根堆中，然后平衡两边的数量关系，保持上面列出的条件。

三、代码实现

1.顺序表排序法实现

import java.util.*;

public class Solution {
    List<Integer> sortedList=new ArrayList<>();
    public void Insert(Integer num) {
        sortedList.add(num);
        sortedList.sort(new Comparator<Integer>(){
            @Override
            public int compare(Integer a,Integer b){
                return a-b;
            }
        });
        System.out.println(sortedList.toString());
    }

    public Double GetMedian() {
        int nowsize=sortedList.size();
        if(nowsize%2==1){
            //奇数元素取中间 
            return (double)sortedList.get(nowsize/2);
        }else{
            double n1=(double)sortedList.get(nowsize/2-1);
            double n2=(double)sortedList.get(nowsize/2);
            return (n1+n2)/2;
        }
    }
}

2.大根堆、小根堆法实现

import java.util.*;

public class Solution {
    //默认建立小根堆，用于存放较大的一半数据，根节点存放这些数据中最小的元素
    PriorityQueue<Integer> minHeap=new PriorityQueue<>();

    //默认建立大根堆，用于存放较小的一半数据，根节点存放这些数据中最大的元素
    PriorityQueue<Integer> maxHeap=new PriorityQueue<>((o1,o2)->o2.compareTo(o1));

    public void Insert(Integer num) {
        minHeap.offer(num);//此时加入的num可能是现有元素较小的一半的数据
        maxHeap.offer(minHeap.poll());//将小根堆中最小元素加入maxHeap
        if(maxHeap.size()>minHeap.size()){//平衡两个堆中的数量
            minHeap.offer(maxHeap.poll());
        }
    }

    public Double GetMedian() {
        double res=0.0;
        if((maxHeap.size()+minHeap.size())%2==0){//偶数个
            res=((double)minHeap.peek()+(double)maxHeap.peek())/2;
        }else{//奇数个，返回minHeap根节点元素
            res=(double)minHeap.peek();
        }
        return res;
    }
}