卷积的计算过程
flyfish
包括手动计算,可视化使用torch.nn.Conv2d实现
示例
import torch
import torch.nn as nn
# 定义输入图像
input_image = torch.tensor([
[1, 2, 3, 0, 1],
[0, 1, 2, 3, 4],
[2, 3, 0, 1, 2],
[1, 2, 3, 4, 0],
[0, 1, 2, 3, 4]
], dtype=torch.float32).unsqueeze(0).unsqueeze(0) # 添加批次和通道维度
print(input_image.shape)
# 定义卷积核
conv_kernel = torch.tensor([
[1, 0, -1],
[1, 0, -1],
[1, 0, -1]
], dtype=torch.float32).unsqueeze(0).unsqueeze(0) # 添加输入和输出通道维度
print(conv_kernel.shape)
# 创建卷积层
conv_layer = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=3, stride=1, padding=0, bias=False)
# 将卷积核的权重设置为自定义值
with torch.no_grad():
conv_layer.weight = nn.Parameter(conv_kernel)
# 进行卷积操作
output_tensor = conv_layer(input_image)
# 打印输入图像
print("输入图像:")
print(input_image.squeeze().numpy())
# 打印卷积核
print("卷积核:")
print(conv_kernel.squeeze().numpy())
# 打印输出结果
print("输出结果:")
print(output_tensor.squeeze().detach().numpy())
torch.Size([1, 1, 5, 5])
torch.Size([1, 1, 3, 3])
# 输入图像:
[[1. 2. 3. 0. 1.]
[0. 1. 2. 3. 4.]
[2. 3. 0. 1. 2.]
[1. 2. 3. 4. 0.]
[0. 1. 2. 3. 4.]]
卷积核:
[[ 1. 0. -1.]
[ 1. 0. -1.]
[ 1. 0. -1.]]
输出结果:
[[-2. 2. -2.]
[-2. -2. -1.]
[-2. -2. -1.]]
输入图像和卷积核
输入图像
I
I
I:
[
1
2
3
0
1
0
1
2
3
4
2
3
0
1
2
1
2
3
4
0
0
1
2
3
4
]
\begin{bmatrix} 1 & 2 & 3 & 0 & 1 \\ 0 & 1 & 2 & 3 & 4 \\ 2 & 3 & 0 & 1 & 2 \\ 1 & 2 & 3 & 4 & 0 \\ 0 & 1 & 2 & 3 & 4 \\ \end{bmatrix}
1021021321320320314314204
卷积核
K
K
K:
[
1
0
−
1
1
0
−
1
1
0
−
1
]
\begin{bmatrix} 1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1 \\ \end{bmatrix}
111000−1−1−1
手动计算卷积
我们将逐个计算每个位置的卷积结果:
- 位置 (0, 0): [ 1 2 3 0 1 2 2 3 0 ] ⊙ [ 1 0 − 1 1 0 − 1 1 0 − 1 ] = ( 1 ⋅ 1 + 2 ⋅ 0 + 3 ⋅ ( − 1 ) ) + ( 0 ⋅ 1 + 1 ⋅ 0 + 2 ⋅ ( − 1 ) ) + ( 2 ⋅ 1 + 3 ⋅ 0 + 0 ⋅ ( − 1 ) ) = ( 1 − 3 ) + ( − 2 ) + ( 2 ) = − 2 \begin{bmatrix} 1 & 2 & 3 \\ 0 & 1 & 2 \\ 2 & 3 & 0 \\ \end{bmatrix} \odot \begin{bmatrix} 1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1 \\ \end{bmatrix} = (1 \cdot 1 + 2 \cdot 0 + 3 \cdot (-1)) + (0 \cdot 1 + 1 \cdot 0 + 2 \cdot (-1)) + (2 \cdot 1 + 3 \cdot 0 + 0 \cdot (-1)) = (1 - 3) + (-2) + (2) \\= -2 102213320 ⊙ 111000−1−1−1 =(1⋅1+2⋅0+3⋅(−1))+(0⋅1+1⋅0+2⋅(−1))+(2⋅1+3⋅0+0⋅(−1))=(1−3)+(−2)+(2)=−2
- 位置 (0, 1): [ 2 3 0 1 2 3 3 0 1 ] ⊙ [ 1 0 − 1 1 0 − 1 1 0 − 1 ] = ( 2 ⋅ 1 + 3 ⋅ 0 + 0 ⋅ ( − 1 ) ) + ( 1 ⋅ 1 + 2 ⋅ 0 + 3 ⋅ ( − 1 ) ) + ( 3 ⋅ 1 + 0 ⋅ 0 + 1 ⋅ ( − 1 ) ) = 2 + ( 1 − 3 ) + ( 3 − 1 ) = 2 \begin{bmatrix} 2 & 3 & 0 \\ 1 & 2 & 3 \\ 3 & 0 & 1 \\ \end{bmatrix} \odot \begin{bmatrix} 1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1 \\ \end{bmatrix} = (2 \cdot 1 + 3 \cdot 0 + 0 \cdot (-1)) + (1 \cdot 1 + 2 \cdot 0 + 3 \cdot (-1)) + (3 \cdot 1 + 0 \cdot 0 + 1 \cdot (-1)) = 2 + (1 - 3) + (3 - 1) \\= 2 213320031 ⊙ 111000−1−1−1 =(2⋅1+3⋅0+0⋅(−1))+(1⋅1+2⋅0+3⋅(−1))+(3⋅1+0⋅0+1⋅(−1))=2+(1−3)+(3−1)=2
- 位置 (0, 2): [ 3 0 1 2 3 4 0 1 2 ] ⊙ [ 1 0 − 1 1 0 − 1 1 0 − 1 ] = ( 3 ⋅ 1 + 0 ⋅ 0 + 1 ⋅ ( − 1 ) ) + ( 2 ⋅ 1 + 3 ⋅ 0 + 4 ⋅ ( − 1 ) ) + ( 0 ⋅ 1 + 1 ⋅ 0 + 2 ⋅ ( − 1 ) ) = 3 − 1 + 2 − 4 − 2 = − 2 \begin{bmatrix} 3 & 0 & 1 \\ 2 & 3 & 4 \\ 0 & 1 & 2 \\ \end{bmatrix} \odot \begin{bmatrix} 1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1 \\ \end{bmatrix} = (3 \cdot 1 + 0 \cdot 0 + 1 \cdot (-1)) + (2 \cdot 1 + 3 \cdot 0 + 4 \cdot (-1)) + (0 \cdot 1 + 1 \cdot 0 + 2 \cdot (-1)) = 3 - 1 + 2 - 4 - 2 \\= -2 320031142 ⊙ 111000−1−1−1 =(3⋅1+0⋅0+1⋅(−1))+(2⋅1+3⋅0+4⋅(−1))+(0⋅1+1⋅0+2⋅(−1))=3−1+2−4−2=−2
- 位置 (1, 0): [ 0 1 2 2 3 0 1 2 3 ] ⊙ [ 1 0 − 1 1 0 − 1 1 0 − 1 ] = ( 0 ⋅ 1 + 1 ⋅ 0 + 2 ⋅ ( − 1 ) ) + ( 2 ⋅ 1 + 3 ⋅ 0 + 0 ⋅ ( − 1 ) ) + ( 1 ⋅ 1 + 2 ⋅ 0 + 3 ⋅ ( − 1 ) ) = − 2 + 2 + 1 − 3 = − 2 \begin{bmatrix} 0 & 1 & 2 \\ 2 & 3 & 0 \\ 1 & 2 & 3 \\ \end{bmatrix} \odot \begin{bmatrix} 1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1 \\ \end{bmatrix} = (0 \cdot 1 + 1 \cdot 0 + 2 \cdot (-1)) + (2 \cdot 1 + 3 \cdot 0 + 0 \cdot (-1)) + (1 \cdot 1 + 2 \cdot 0 + 3 \cdot (-1)) = -2 + 2 + 1 - 3 \\= -2 021132203 ⊙ 111000−1−1−1 =(0⋅1+1⋅0+2⋅(−1))+(2⋅1+3⋅0+0⋅(−1))+(1⋅1+2⋅0+3⋅(−1))=−2+2+1−3=−2
- 位置 (1, 1): [ 1 2 3 3 0 1 2 3 4 ] ⊙ [ 1 0 − 1 1 0 − 1 1 0 − 1 ] = ( 1 ⋅ 1 + 2 ⋅ 0 + 3 ⋅ ( − 1 ) ) + ( 3 ⋅ 1 + 0 ⋅ 0 + 1 ⋅ ( − 1 ) ) + ( 2 ⋅ 1 + 3 ⋅ 0 + 4 ⋅ ( − 1 ) ) = 1 − 3 + 3 − 1 + 2 − 4 = − 2 \begin{bmatrix} 1 & 2 & 3 \\ 3 & 0 & 1 \\ 2 & 3 & 4 \\ \end{bmatrix} \odot \begin{bmatrix} 1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1 \\ \end{bmatrix} \begin{aligned} \\ &= (1 \cdot 1 + 2 \cdot 0 + 3 \cdot (-1)) + (3 \cdot 1 + 0 \cdot 0 + 1 \cdot (-1)) + (2 \cdot 1 + 3 \cdot 0 + 4 \cdot (-1)) \\ &= 1 - 3 + 3 - 1 + 2 - 4 \\ &= -2\end{aligned} 132203314 ⊙ 111000−1−1−1 =(1⋅1+2⋅0+3⋅(−1))+(3⋅1+0⋅0+1⋅(−1))+(2⋅1+3⋅0+4⋅(−1))=1−3+3−1+2−4=−2
- 位置 (1, 2): [ 2 3 4 0 1 2 3 4 0 ] ⊙ [ 1 0 − 1 1 0 − 1 1 0 − 1 ] = ( 2 ⋅ 1 + 3 ⋅ 0 + 4 ⋅ ( − 1 ) ) + ( 0 ⋅ 1 + 1 ⋅ 0 + 2 ⋅ ( − 1 ) ) + ( 3 ⋅ 1 + 4 ⋅ 0 + 0 ⋅ ( − 1 ) ) = − 2 − 2 + 3 = − 1 \begin{bmatrix} 2 & 3 & 4 \\ 0 & 1 & 2 \\ 3 & 4 & 0 \\ \end{bmatrix} \odot \begin{bmatrix} 1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1 \\ \end{bmatrix} \\ = (2 \cdot 1 + 3 \cdot 0 + 4 \cdot (-1)) + (0 \cdot 1 + 1 \cdot 0 + 2 \cdot (-1)) + (3 \cdot 1 + 4 \cdot 0 + 0 \cdot (-1)) \\ = -2 - 2 + 3 \\ = -1 203314420 ⊙ 111000−1−1−1 =(2⋅1+3⋅0+4⋅(−1))+(0⋅1+1⋅0+2⋅(−1))+(3⋅1+4⋅0+0⋅(−1))=−2−2+3=−1
- 位置 (2, 0): [ 2 3 0 1 2 3 0 1 2 ] ⊙ [ 1 0 − 1 1 0 − 1 1 0 − 1 ] = ( 2 ⋅ 1 + 3 ⋅ 0 + 0 ⋅ ( − 1 ) ) + ( 1 ⋅ 1 + 2 ⋅ 0 + 3 ⋅ ( − 1 ) ) + ( 0 ⋅ 1 + 1 ⋅ 0 + 2 ⋅ ( − 1 ) ) = 2 + ( 1 − 3 ) − 2 = − 2 \begin{bmatrix} 2 & 3 & 0 \\ 1 & 2 & 3 \\ 0 & 1 & 2 \\ \end{bmatrix} \odot \begin{bmatrix} 1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1 \\ \end{bmatrix} = (2 \cdot 1 + 3 \cdot 0 + 0 \cdot (-1)) + (1 \cdot 1 + 2 \cdot 0 + 3 \cdot (-1)) + (0 \cdot 1 + 1 \cdot 0 + 2 \cdot (-1)) \\= 2 + (1 - 3) - 2 \\= -2 210321032 ⊙ 111000−1−1−1 =(2⋅1+3⋅0+0⋅(−1))+(1⋅1+2⋅0+3⋅(−1))+(0⋅1+1⋅0+2⋅(−1))=2+(1−3)−2=−2
- 位置 (2, 1):$ [ 3 0 1 2 3 4 1 2 3 ] ⊙ [ 1 0 − 1 1 0 − 1 1 0 − 1 ] = ( 3 ⋅ 1 + 0 ⋅ 0 + 1 ⋅ ( − 1 ) ) + ( 2 ⋅ 1 + 3 ⋅ 0 + 4 ⋅ ( − 1 ) ) + ( 1 ⋅ 1 + 2 ⋅ 0 + 3 ⋅ ( − 1 ) ) = 3 − 1 + 2 − 4 + 1 − 3 = − 2 \begin{bmatrix} 3 & 0 & 1 \\ 2 & 3 & 4 \\ 1 & 2 & 3 \\ \end{bmatrix} \odot \begin{bmatrix} 1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1 \\ \end{bmatrix} \\= (3 \cdot 1 + 0 \cdot 0 + 1 \cdot (-1)) + (2 \cdot 1 + 3 \cdot 0 + 4 \cdot (-1)) + (1 \cdot 1 + 2 \cdot 0 + 3 \cdot (-1)) = 3 - 1 + 2 - 4 + 1 - 3 \\= -2 321032143 ⊙ 111000−1−1−1 =(3⋅1+0⋅0+1⋅(−1))+(2⋅1+3⋅0+4⋅(−1))+(1⋅1+2⋅0+3⋅(−1))=3−1+2−4+1−3=−2
- 位置 (2, 2): [ 0 1 2 3 4 0 2 3 4 ] ⊙ [ 1 0 − 1 1 0 − 1 1 0 − 1 ] = ( 0 ⋅ 1 + 1 ⋅ 0 + 2 ⋅ ( − 1 ) ) + ( 3 ⋅ 1 + 4 ⋅ 0 + 0 ⋅ ( − 1 ) ) + ( 2 ⋅ 1 + 3 ⋅ 0 + 4 ⋅ ( − 1 ) ) = − 2 + 3 + 2 − 4 = − 1 \begin{bmatrix} 0 & 1 & 2 \\ 3 & 4 & 0 \\ 2 & 3 & 4 \\ \end{bmatrix} \odot \begin{bmatrix} 1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1 \\ \end{bmatrix} \\= (0 \cdot 1 + 1 \cdot 0 + 2 \cdot (-1)) + (3 \cdot 1 + 4 \cdot 0 + 0 \cdot (-1)) + (2 \cdot 1 + 3 \cdot 0 + 4 \cdot (-1)) \\= -2 + 3 + 2 - 4 \\= -1 032143204 ⊙ 111000−1−1−1 =(0⋅1+1⋅0+2⋅(−1))+(3⋅1+4⋅0+0⋅(−1))+(2⋅1+3⋅0+4⋅(−1))=−2+3+2−4=−1
参数解释
conv_layer = nn.Conv2d(
in_channels=3, # 输入通道数
out_channels=16, # 输出通道数
kernel_size=3, # 卷积核大小
stride=1, # 步幅
padding=1, # 填充
padding_mode='zeros', # 填充模式
dilation=1, # 空洞卷积
groups=1, # 组卷积
bias=True # 是否使用偏置
)
in_channels (int): 输入通道数。例如,对于RGB图像,in_channels 应为 3。
out_channels (int): 输出通道数,也就是卷积核的数量。
kernel_size (int or tuple): 卷积核的大小。如果是整数,表示卷积核的高度和宽度相等。如果是元组,表示 (高度, 宽度)。
stride (int or tuple, optional): 卷积操作中窗口滑动的步幅。如果是整数,表示高度和宽度的步幅相等。如果是元组,表示 (高度步幅, 宽度步幅)。默认值为 1。
padding (int or tuple, optional): 输入的每一边要填充的零的层数。如果是整数,表示高度和宽度的填充相等。如果是元组,表示 (高度填充, 宽度填充)。默认值为 0。
padding_mode (str, optional): 填充模式,可以是 'zeros', 'reflect', 'replicate' 或 'circular'。默认值为 'zeros'。
dilation (int or tuple, optional): 卷积核元素之间的间距。如果是整数,表示高度和宽度的间距相等。如果是元组,表示 (高度间距, 宽度间距)。默认值为 1。
groups (int, optional): 从输入通道到输出通道的阻塞连接数。默认值为 1。groups 可以用于实现深度可分离卷积。
bias (bool, optional): 如果设置为 True,则添加一个学习到的偏置。默认值为 True。
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as patches
from matplotlib.animation import FuncAnimation, PillowWriter
# 定义输入图像和卷积核
input_image = np.array([
[1, 2, 3, 0, 1],
[0, 1, 2, 3, 4],
[2, 3, 0, 1, 2],
[1, 2, 3, 4, 0],
[0, 1, 2, 3, 4]
])
conv_kernel = np.array([
[1, 0, -1],
[1, 0, -1],
[1, 0, -1]
])
# 输入图像和卷积核的尺寸
input_size = input_image.shape[0]
kernel_size = conv_kernel.shape[0]
output_size = input_size - kernel_size + 1
# 创建图形和轴
fig, ax = plt.subplots(figsize=(6, 6))
# 显示输入图像
im = ax.imshow(input_image, cmap='viridis')
# 初始化矩形框和文本
rect = patches.Rectangle((0, 0), kernel_size, kernel_size, linewidth=2, edgecolor='r', facecolor='none')
ax.add_patch(rect)
text = ax.text(0, 0, '', ha='center', va='center', color='white', fontsize=12)
# 动画更新函数
def update(frame):
i, j = divmod(frame, output_size)
sub_matrix = input_image[i:i+kernel_size, j:j+kernel_size]
conv_result = np.sum(sub_matrix * conv_kernel)
# 更新矩形框的位置
rect.set_xy((j, i))
# 更新文本的位置和内容
text.set_position((j + kernel_size / 2, i + kernel_size / 2))
text.set_text(f'{conv_result:.2f}')
return im, rect, text
# 创建动画
ani = FuncAnimation(fig, update, frames=output_size * output_size, blit=True, repeat=False)
# 保存动画为 GIF 文件
ani.save('convolution_animation.gif', writer=PillowWriter(fps=1))
plt.show()
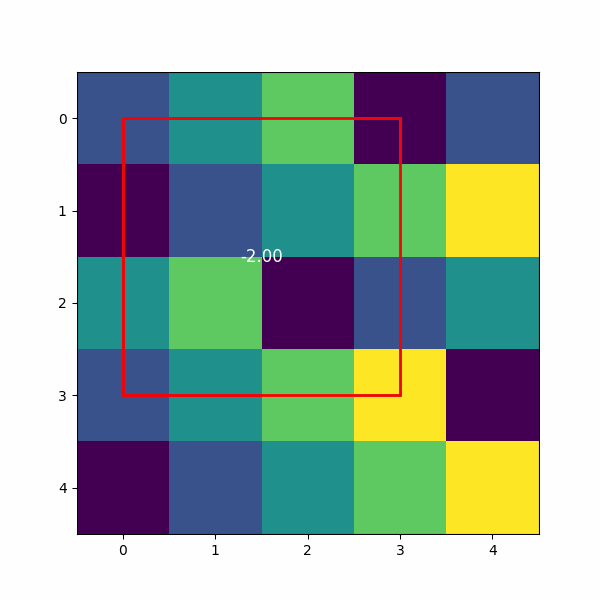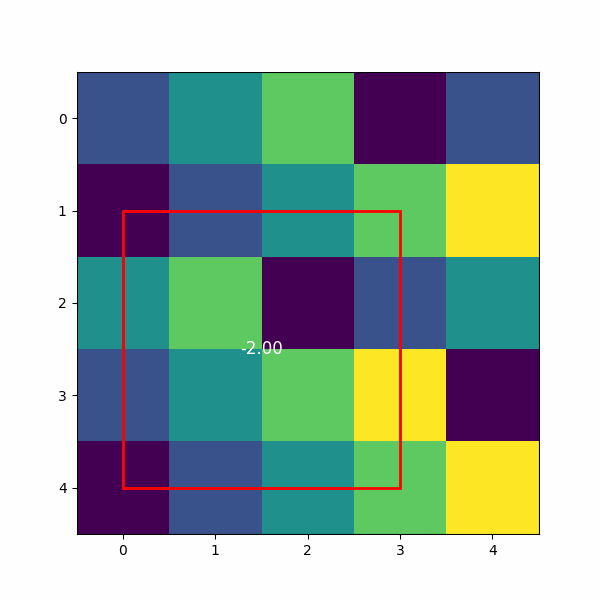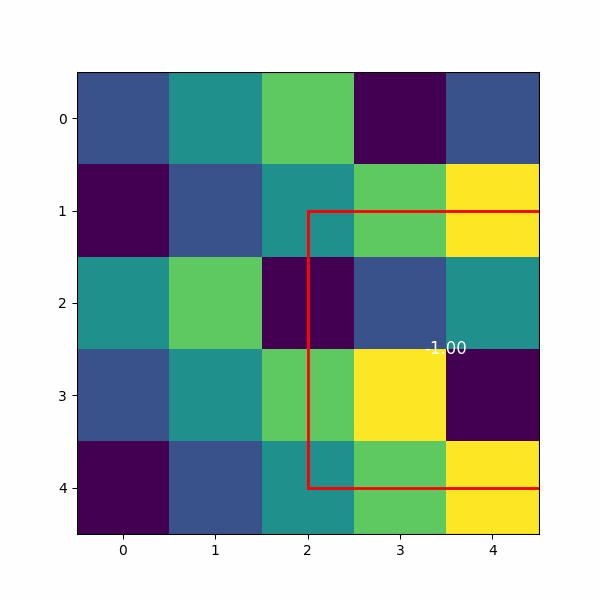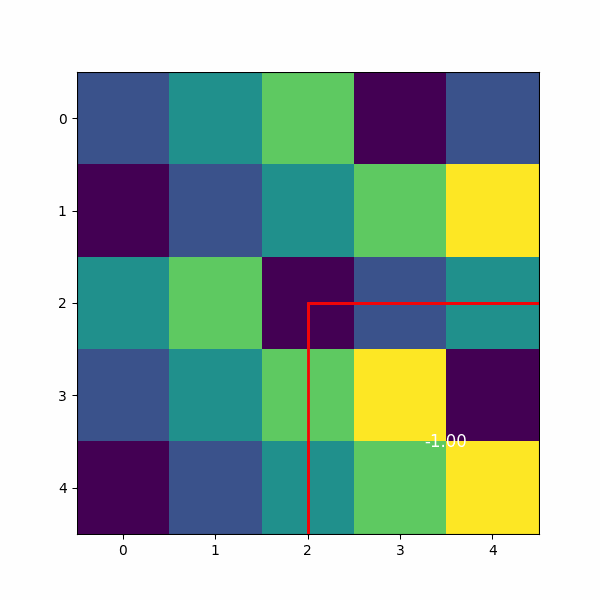
卷积的结果
[[-2. 2. -2.]
[-2. -2. -1.]
[-2. -2. -1.]]