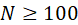目录
一、最小生成树(Prime算法)
1)概念
2)最小生成树的应用
3)最小生成树的创建
4)代码实现
五、最短路径
1)Dijkstra算法
Question:
六、拓扑排序
1)概念
2)拓扑排序算法思想
3)代码实现
上一章的内容:
【数据结构】十、图的存储方式以及BFS、DFS遍历算法-CSDN博客
本章的实验用图仍然不变(无向带权图,用于前两个算法):

一、最小生成树(Prime算法)
1)概念
设存在一个具有n个顶点的图,顶点之间存在着许多条边,从这些边中一定可以取出
n-1条边形成一棵树,若连接这棵树的节点的边的权值之和最小,则这棵树是最小生成树。
2)最小生成树的应用
要在n个城市之间铺设光缆,主要目标是要使这 n 个城市的任意两个之间都可以通信,但铺设光缆的费用很高,且各个城市之间铺设光缆的费用不同,因此另一个目标是要使铺设光缆的总费用最低。这就需要找到带权的最小生成树。
3)最小生成树的创建
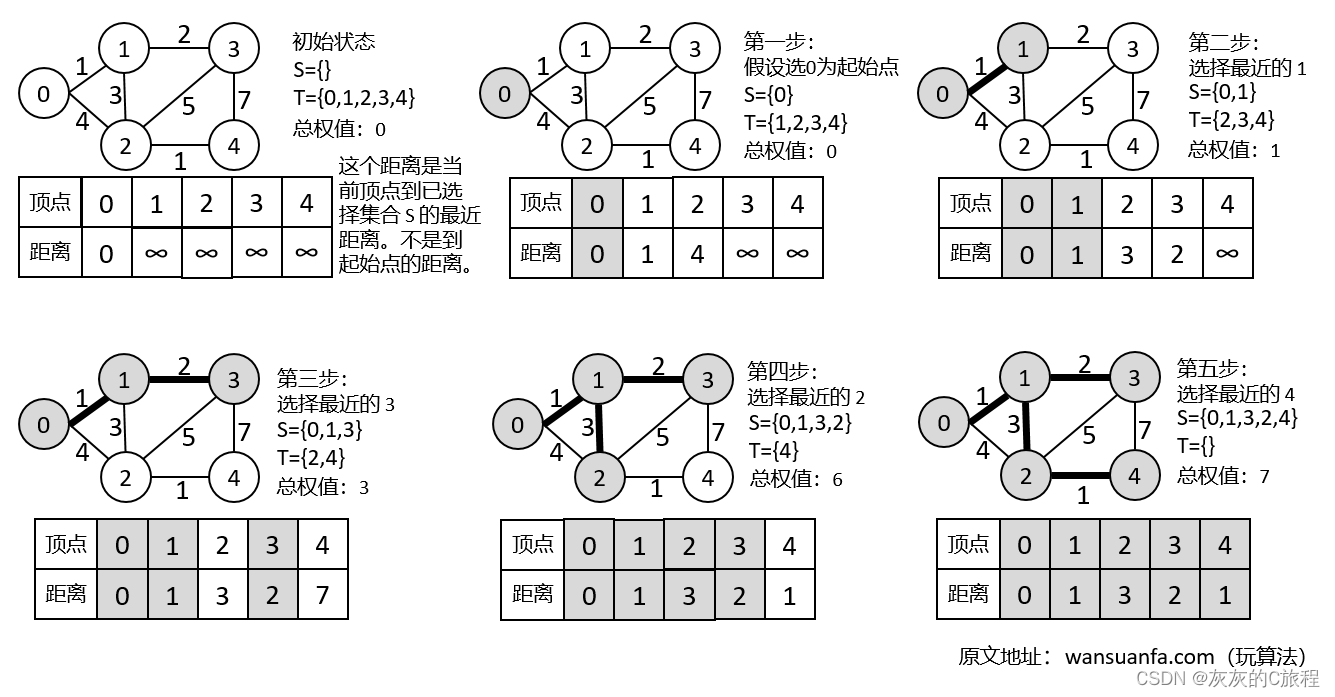
第一步:首先我们先创建一个数组lowCost,用来存放到每个顶点的最短的距离,数组的下标即表示顶点的序号。由于一开始我们没有访问任何节点,所以先初始化到每个顶点的距离为无穷大。
第二步:然后我们从一个初始节点开始,将该节点对应的最短距离设置为0(自身到自身的距离为0)并标记已访问,遍历该顶点的邻接顶点,更新lowCost数组中的最短距离。
第三步:遍历lowCost数组,找出lowCost数组中的最小值对应的节点,标记访问。
第四步:回到第二步,更新lowCost数组,继续寻找,直到所有顶点遍历完成。
算法如下图所示:其中灰色的表示已访问的顶点,T为未访问的顶点,S中为已访问的节点。
4)代码实现
这里我不仅要计算最小生成树的权值之和,还要记录下生成的最小生成树的边的顺序(包括弧头和弧尾)。
让我们先建立一个结构体用来存放以上数据:
typedef struct {
char vertex; //存放弧头节点
char tail; //存放每条边的弧尾节点
int weight; //存放权值
}MinSpanTree;
Prime算法本法:
//Prime算法
//closeVertex数组用来保存n个顶点和n-1条边,其顺序即为最小生成树的构造顺序
void Prime(AdjMGraph G, MinSpanTree closeVertex[])
{
int* lowCost = (int*)malloc(G.node.size * sizeof(int)); //创建一个数组用来记录已访问的顶点所连接的最小边的权值
if (lowCost == NULL)
{
printf("内存分配失败!\n");
return;
}
for (int i = 0; i < G.node.size; i++) //先初始化为邻接矩阵第一行的值
{
lowCost[i] = G.edge[0][i];
}
closeVertex[0].tail = G.node.list[0];
lowCost[0] = -1; //标记已访问节点,保证每个顶点只访问一次
for (int i = 1; i < G.node.size; i++) //每次循环找出已访问节点中连接的最小权值的边以及该边连接的节点
{
int minweight = MAXWEIGHT; //与上一个点连接的边的最小权值
int minnode = 0; //记录该边另一头的节点
for (int j = 0; j < G.node.size; j++) //遍历与该顶点相邻的未访问节点,找到最小边
{
if (lowCost[j] > 0 && lowCost[j] < minweight) // >0涵盖了自身节点和已访问的节点
{
minweight = lowCost[j];
minnode = j;
}
}
closeVertex[i].weight = minweight; //记录边的权值
closeVertex[i].tail = G.node.list[minnode]; //记录尾节点
for (int t = 0; t < G.node.size; t++) //寻找头节点
{
if (G.edge[t][minnode] == minweight)
{
closeVertex[i].vertex = G.node.list[t];
break;
}
}
lowCost[minnode] = -1; //标记
for (int k = 0; k < G.node.size; k++)
{
if (G.edge[minnode][k] < lowCost[k]) lowCost[k] = G.edge[minnode][k]; //更新最短边
}
}
//输出最小生成树的顶点和权值序列
printf("初始顶点:%c\n", closeVertex[0].tail);
for (int i = 1; i < G.node.size; i++)
{
printf("%c-%c-%d\n",closeVertex[i].vertex, closeVertex[i].tail, closeVertex[i].weight);
}
}
运行结果如下:
二、最短路径
1)Dijkstra算法
Dijkstra算法:求每个顶点到其余各顶点的最短路径。
算法思想:
首先我们创建一个dist数组,用于存储该节点到其他节点的最短路径,还需要一个visited数组记录该节点是否被访问,由于我们还需要记录下路径,因此再创建一个parent数组,表示每个节点的父节点。
第一步:从初始节点开始,标记初始节点已访问;
第二步:遍历邻接矩阵,找到该节点的邻接节点,更新dist数组的最短距离,并将邻接节点的父节点记录下来;
第三步:执行n-1次循环(因为最多需要n-1次才能找到所有节点,该情况为一个线性图),得到其余点的最短距离。
代码如下:
void dijkstra(AdjMGraph* G, int src) {
int n = G->node.size;
int* dist = (int*)malloc(n * sizeof(int)); // 存储源节点到各节点的最短距离
int *visited = (int*)malloc(n * sizeof(int)); // 记录节点是否已经访问
int *parent = (int*)malloc(n * sizeof(int)); // 记录最短路径上的父节点
if (dist == NULL || visited == NULL || parent == NULL)
{
printf("内存分配失败!\n");
return;
}
// 初始化
for (int i = 0; i < n; i++) {
dist[i] = MAXWEIGHT;
visited[i] = 0;
parent[i] = -1;
}
dist[src] = 0;
// 找到最短路径
for (int count = 0; count < n - 1; count++) { //找到该顶点到其余n-1个顶点的路径
int u, minDist = MAXWEIGHT;
// 选择当前未访问的节点中距离最小的节点
for (int v = 0; v < n; v++) {
if (!visited[v] && dist[v] < minDist) {
minDist = dist[v];
u = v;
}
}
visited[u] = 1;
// 更新从源节点到u的相邻节点的距离
for (int v = 0; v < n; v++) {
if (!visited[v] && G->edge[u][v] != MAXWEIGHT && G->edge[u][v] != 0 && dist[u] != MAXWEIGHT &&
dist[u] + G->edge[u][v] < dist[v]) {
dist[v] = dist[u] + G->edge[u][v];
parent[v] = u; //v的父节点为u
}
}
}
// 输出最短路径
printf("节点 最短距离 最短路径\n");
for (int i = 0; i < n; i++) {
printf("%c \t %d\t\t", G->node.list[i], dist[i]);
int p = i;
printf("%c", G->node.list[p]);
while (parent[p] != -1) {
printf(" <- %c", G->node.list[ parent[p] ]);
p = parent[p];
}
printf("\n");
}
free(dist);
free(parent);
free(visited);
}
说明:visited数组其实有一个节点未标记访问,因为循环只执行了n-1次;
代码运行结果如下:

Question:
这里的
parent数组比较有意思,也比较难以理解,明明是同一个数组,为什么可以做到根据不同的末节点输出整条路径?
以A作为原点,让我们输出看看此时parent数组的数据:
![]()
很明显parent数组存放的是存放顶点数据的线性表的下标索引,但是这好像还是看不出来什么,让我们转换一下:
parent数组的下标: 0 1 2 3 4 5 6 7 8 9
parent存放的数据: -1 0 0 1 3 3 2 4 5 6
顶点顺序: A B C D E F G H I J
对应顶点: A A B D D C E F G
对于parent数组,第一个-1,表示A节点自身,不用管。第二个数据表示的是B顶点,其值为0,0代表的是A节点的索引,表示B顶点的父节点为A;同样的,第三个数据表示C节点,也是如此;直接看第五个位置吧,第五个位置代表E节点,其值为3,3代表节点E,然后下标3对应的数据是1,1代表节点B,然后下标1对应的数据是0,0代表节点A,因此A到E的路径为A→B→D→E。
换句话说,parent数组存放的是对应节点的父节点的索引。
三、拓扑排序
1)概念
在图论中,拓扑排序是将有向无环图的所有节点按特点的规律进行线性排序,其中:
-
每个顶点出现且只出现一次。
-
若存在一条从顶点 A 到顶点 B 的路径,那么在序列中顶点 A 出现在顶点 B 的前面。
在实际应用中,有向无环图可以代表工作内容的先后条件,边的弧头节点表示必须要先完成的工作,才能去完成该边的弧尾节点的工作,将该图进行排序,则得到一个工作流程。
2)拓扑排序算法思想
第一步:寻找一个没有入度的节点;
第二步:将该节点输出,并将该顶点的邻接顶点的入度减一;
第三步:重复第一第二步,直到所有节点输出。
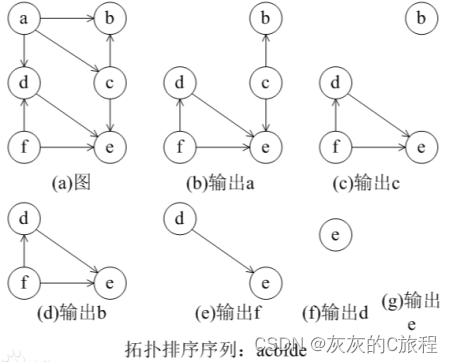
tips:拓扑排序的序列不是唯一的,这取决于对应的算法,比如上图中也可以从f节点开始。
3)代码实现
//求各顶点的入度并保存到数组中
static void InDegree(AdjMGraph* G,int In_Degree[])
{
for (int i = 0; i < G->node.size; i++)
{
for (int j = 0; j < G->node.size; j++)
{
if (G->edge[j][i] != MAXWEIGHT && G->edge[j][i] != 0)
In_Degree[i]++;
}
}
}
// 拓扑排序函数
void topologicalSort(AdjMGraph* G) {
int n = G->node.size;
int* In_Degree = (int*)calloc(n , sizeof(int)); //存放每个顶点的入度信息,calloc函数可以帮助我们初始化
int* Sort = (int*)calloc(n , sizeof(int)); //存放拓扑排序的序列
if (In_Degree == NULL || Sort == NULL)
{
printf("内存分配失败!\n");
return;
}
InDegree(G, In_Degree);
int k = 0; //Sort数组下标
while(k<n)
{
for (int i = 0; i < n; i++)
{
if (In_Degree[i] == 0) //找到第一个入度为0的节点
{
Sort[k++] = i;
for (int j = 0; j < n; j++) //将该节点的邻接顶点入度减1
{
if (G->edge[i][j] != MAXWEIGHT && G->edge[i][j] != 0)
{
In_Degree[j]--;
}
}
In_Degree[i] = -1; //标记为已访问
break;
}
}
}
for (int i = 0; i < n; i++)
{
printf("%c ", G->node.list[Sort[i]]);
}
}
对应上图,输出结果如下:
![]()
以上就是今天分享的全部内容,最后感谢你观看完我的文章,如果文章对你有帮助,可以点赞收藏评论,这是对作者最好的鼓励!不胜感激🥰