【十大排序算法】快速排序

news2024/11/29 0:38:04

在乱序的世界中，快速排序如同一位智慧的园丁，
以轻盈的手法，将无序的花朵们重新安排，
在每一次比较中，沐浴着理性的阳光，
终使它们在有序的花园里，开出绚烂的芬芳。

文章目录

一、快速排序
二、发展历史
三、处理流程
四、算法实现
五、快速排序的特性
六、小结
推荐阅读

一、快速排序

快速排序是一种高效的排序算法，它采用了分治的策略。它的基本思想是选择一个基准值，将数组分为两个子数组，一个子数组中的所有元素都小于基准值，另一个子数组中的所有元素都大于基准值，然后对这两个子数组递归地进行排序。

具体来说，快速排序的步骤如下：

选择一个基准值（通常是数组的第一个元素、最后一个元素或者中间元素）。
将数组分为两个子数组，一个子数组中的所有元素都小于基准值，另一个子数组中的所有元素都大于基准值。
对这两个子数组递归地进行排序。
将排好序的子数组合并起来，即得到有序数组。

快速排序的关键在于分割操作，通过这个操作，它可以将一个大问题分解成两个规模较小的子问题，然后分别解决，最终达到整体有序的目的。

二、发展历史

快速排序是由英国计算机科学家 Tony Hoare 在 $1960$ 年代提出的。Hoare 最初将这一算法称为 “分区交换排序”，后来更广泛地称为快速排序。他的灵感来自于合并排序和插入排序。

早期思想： Hoare 注意到合并排序在实践中性能良好，但需要额外内存空间；而插入排序则内存消耗较少，但在大规模数据下性能不佳。他希望能够结合两者的优点，创造出一种既能够节省空间又能够在平均情况下具有良好性能的排序算法。
Hoare 分区法： Hoare 提出了一种称为 Hoare 分区法的分区策略，这成为了快速排序的核心部分。这个方法从数组中选择一个基准值，将数组分成两个部分，左边的部分包含比基准值小的元素，右边的部分包含比基准值大的元素。然后，递归地对这两个部分进行排序。
论文发表： Hoare 在 $1961$ 年发表了关于快速排序的论文，论文中描述了这一算法的基本原理和实现方法。此后，他不断改进和优化这一算法，使得快速排序成为了一种非常高效的排序算法。
持续优化： 随着计算机科学的发展，许多学者对快速排序进行了进一步的优化和改进。例如，采用随机化的方式选择基准值，以防止最坏情况的发生；使用三数取中法来选择基准值，以提高算法的稳定性和性能等。
现代应用： 至今，快速排序仍然是一种非常流行和高效的排序算法，被广泛应用于各种编程语言和实际应用中。其简洁而优雅的设计理念以及优秀的性能使得它成为了排序算法中的经典之作。

三、处理流程

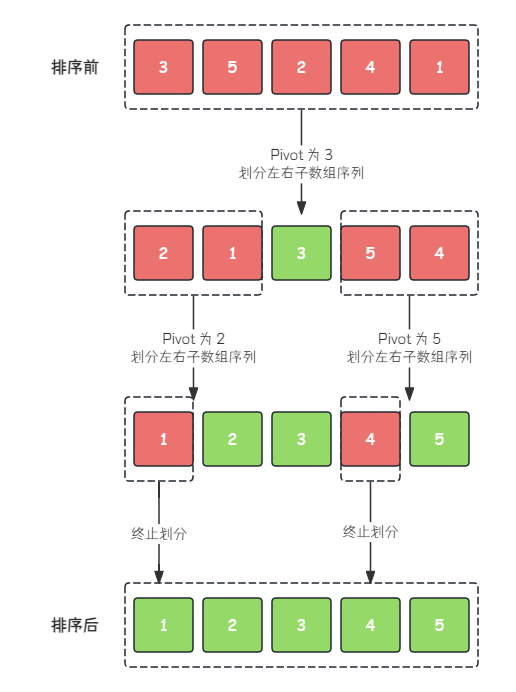
场景假设：我们需要将下列无序序列使用快速排序按从小到大进行排序。

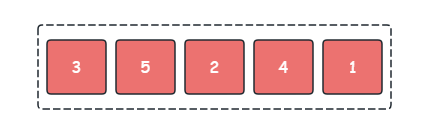
快速排序的流程如下：

在原序列中选取第一个元素 $3$ 作为 Pivot 哨兵
将序列中小于 Pivot 的元素，放在 Pivot 的左边，大于 Pivot 的元素放在 Pivot 的右边
递归处理 Pivot 左边的序列和右边的序列
当子序列为长度 $1$ 时终止

workspace (1).png

四、算法实现

// 快速排序入口
void quickSort(int[] arr, int low, int high) {
    if (low < high) {
        // 对数组进行分区操作
        int pivot = partition(arr, low, high);
        // 递归排序左半部分
        quickSort(arr, low, pivot - 1);
        // 递归排序右半部分
        quickSort(arr, pivot + 1, high);
    }
}

// 分区操作
int partition(int[] arr, int low, int high) {
    // 选择最后一个元素作为 pivot
    int pivot = arr[high];
    int i = low - 1; // 指向小于 pivot 的区域的边界

    // 遍历数组，将小于 pivot 的元素放到左侧
    for (int j = low; j < high; j++) {
        if (arr[j] < pivot) {
            i++;
            // 交换元素
            int temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
        }
    }

    // 将 pivot 放到正确位置
    int temp = arr[i + 1];
    arr[i + 1] = arr[high];
    arr[high] = temp;

    // 返回 pivot的位置
    return i + 1;
}

public static void main(String[] args) {
    int[] arr = {5, 3, 8, 6, 2, 7, 1, 4};
    // 调用快速排序算法
    quickSort(arr, 0, arr.length - 1);

    // 输出排序后的数组
    System.out.print("Sorted array: ");
    for (int num : arr) {
        System.out.print(num + " ");
    }
}

算法时间复杂度分析：

情况	时间复杂度	计算公式	公式解释
最好情况	$O (n l o g n)$	$2T(\frac{n}{2}) + n$	在最优情况下，每次划分都能将数组均匀地分成两部分。因此，我们有两个大小为 $\frac{n}{2}$ 的子问题，所以有 $2T(\frac{n}{2})$ 。然后，我们需要 $n$ 的时间来进行划分操作。所以，总的时间复杂度就是 $2T(\frac{n}{2}) + n$
平均情况	$O (n l o g n)$	$T(\frac{n}{2}) + T(\frac{n}{2}) + n$	在平均情况下，我们假设每次划分都能将数组均匀地分成两部分。因此，我们有两个大小为 $\frac{n}{2}$ 的子问题，所以有 $T(\frac{n}{2}) + T(\frac{n}{2})$ 。然后，我们需要 $n$ 的时间来进行划分操作。所以，总的时间复杂度就是 $T(\frac{n}{2}) + T(\frac{n}{2}) + n$
最坏情况	$O(n^2)$	$T (n) = T (n - 1) + n$	在最坏情况下，每次划分只能将数组划分为一份有 $n - 1$ 个元素，另一份有 $0$ 个元素。因此，我们有一个大小为 $n - 1$ 子问题，所以有 $T (n - 1)$ 。然后，我们需要 $n$ 的时间来进行划分操作。所以，总的时间复杂度就是 $T (n - 1) + n$