目录
平衡二叉树的定义
平衡二叉树的基本操作
查找
插入
AVL树的建立
平衡二叉树的定义
平衡二叉树仍然是一棵二叉查找树,只是在其基础上增加了平衡的要求,也就是其左右子树的高度之差的绝对值不超过1。
在定义树的结构时需要加入一个变量height,用来记录以当前结点为根节点的子树的高度。
struct node{
int v,height;
node *lchild,*rchild;
};在这种定义下,如果需要新建一个结点,就可以使用如下写法:
node* newNode(int v){
node* Node=new node;
Node->v=v;
Node->height=1;
Node->lchild=Node->rchild=NULL;
return Node;
}显然,可以通过下面的函数获取结点root所在子树的当前高度:
int getheight(node* root){
if(root==NULL){
return 0;
}
return root->height;
}于是根据定义,就可以通过下面的函数计算左右子树的高度差:
int getbalancefactor(node* root){
return getheight(root->lchild)-getheight(root->rchild);
}显然,结点root所在子树的高度等于其左右子树高度的较大值加1.
void updateheight(node* root){
root->height=max(getheight(root->lchild),getrchild(root->rchild))+1;
}平衡二叉树的基本操作
查找
void search(node* root,int x){
if(root==NULL){
printf("search failed\n");
return;
}
if(x==root->data){
printf("%d\n",root->data);
}
else if(x<root->data){
search(root->lchild,x);
}
else{
search(root->rchild,x);
}
}插入
左旋的代码

void L(node* &root){
node* temp=root->rchild;
root->rchild=temp->lchild;
temp->lchild=root;
updataheight(root);
updataheight(temp);
root=temp;
}右旋的代码
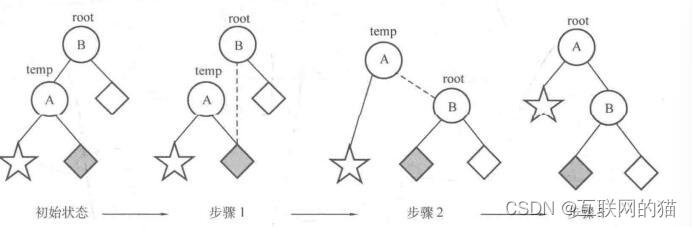
void R(node* &root){
node* temp=root->lchild;
root->lchild=temp->rchild
temp->rchild=root;
updataheight(root);
updataheight(temp);
root=temp;
}对于各种树型使用的操作如下:

首先,AVL树的插入代码是在二叉查找树的插入代码的基础上增加平衡操作的,因此,如果不考虑平衡操作,代码是下面这样的:
void insert(node* &root,int v){
if(root==NULL){
root=newNode(v);
return;
}
if(v<root->data){
insert(root->lchild,v);
}
else{
insert(root->rchild,v);
}
}在这个基础上,由于需要从插入的结点开始从下往下判断结点是否失衡,因此需要在每个insert函数之后更新当前子树的高度,并在这之后根据树型是LL型、LR型、RR型、RL型之一来进行平衡操作。
void insert(node* &root,int v){
if(root==NULL){
root=newNode(v);
return;
}
if(v<root->data){
insert(root->lchild,v);
updataheight(root);
if(getbalancefactor(root)==2){
if(getbalancefactor(root->lchild)==1){//L型
R(root);
}
else if(getbalancefactor(root->lchild)==-1){//LR型
L(root->lchild);
R(root);
}
}
}
else{
insert(root->rchild,v);
updataheight(root);
if(getbalancefactor(root)==-2){
if(getbalancefactor(root->lchild)==-1){//RR型
L(root);
}
else if(getbalancefactor(root->rchild)==1){//RL型
R(root->rchild);
L(root);
}
}
}
}AVL树的建立
node* Create(int data[],int n){
node* root=NULL;
for(int i=0;i<n;i++){
insert(root,data[i]);
}
return root;
}