线上OJ 地址：

【03NOIP普及组】数字游戏

此题考察的是 区间DP + 前缀和

核心思想：

1、这道题主要考查了动态规划的思想。通过分析题目，可以发现需要 枚举环上所有划分为m组 的不同方案，来求得最大或最小值。属于 环上动态规划 问题，可以 破环成链，变成区间dp问题。

备注：

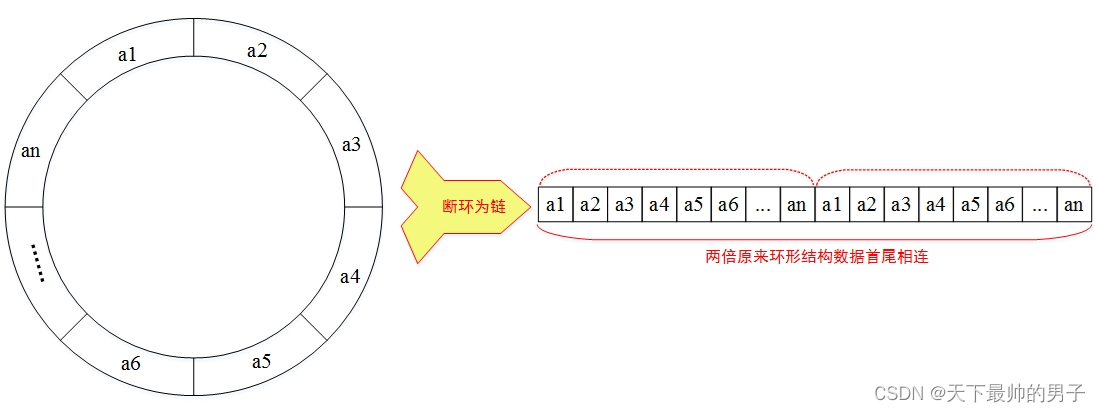
环形 结构上的动态规划问题，是一种特殊的区间动态规划问题。由于存在 环形后效性，所以 不满足动态规划算法 的 无后效性 约束条件。故常将环形结构上的动态规划问题，通过 “断环为链” 策略 转化为线性动态规划 问题求解。
断环为链 策略具体来说就是“ 把环断开为链，然后复制一倍接在末尾 ”，通过这种方式可以将环形结构上的动态规划问题转化为线性结构上的动态规划问题，然后使用线性动态规划的方法进行求解。本段引用。

2、在本题中，
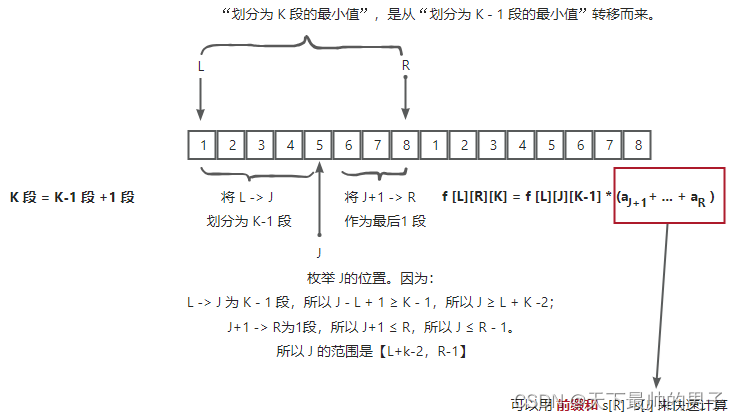
2.1 设置状态 f[L][R][K] 表示从 L 到 R 这段长度为 R - L + 1 的连续序列划分为 K 组的 最小值;
2.2 设置状态 b[L][R][K] 表示从 L 到 R 这段长度为 R - L + 1 的连续序列划分为 k 组的 最大值;

因为 划分为 K 段的最小值 ，是从 划分为 K - 1 段的最小值 转移而来。即 f[K] = f[K-1] * 最后一段数值和

注解：
如上图所示，设左区间端点是L，右区间端点是R，在L和R之间找一点 J来区分最后一段。我们枚举 J的位置。
因为：
1、L -> J 为 K - 1 段，所以 $J-L+1\ge K-1$，所以 $J\ge L+K-2$；
2、J+1 -> R为最后1段，所以 $J+1\le R$，所以 $J\le R-1$。
所以 J 的范围是 $J\in [L+k-2，R-1]$

所以动态转移方程为：

$f[L][R][K]=min(f[L][R][K],f[L][J][K-1]\ast (a_{J+1}+...+a_R))$;
$b[L][R][K]=max(b[L][R][K],b[L][J][K-1]\ast (a_{J+1}+...+a_R))$;

为了快速计算，我们记 s[n] 为前 n 项的 前缀和 数组，则上式中的 $a_{J+1}+...+a_R=s[R]-s[J]$ 。

题解代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 110, M = 10;   // N = 2*n + 余量。n上限为50 
const int INF = 0x3f3f3f3f;  // 无穷大 
const int NINF = 0xafafafaf; // 无穷小 

int n, m;
int a[N], s[N]; // a[]为数值；s[]为前缀和 
int f[N][N][M]; // f[L][R][K] 表示从 L 到 R 这段长度为 R - L + 1 的连续序列划分为 K 组的最小值 
int b[N][N][M]; // b[L][R][K] 表示从 L 到 R 这段长度为 R - L + 1 的连续序列划分为 k 组的最大值;
int max_ans = NINF;  
int min_ans = INF;    

// 计算 num对 10的模。如果是负数，需转成整数 
int get_mod(int num)  
{
    return (num % 10 + 10) % 10; // 调整负数模为非负整数     
}

int main()
{
    scanf("%d %d", &n, &m);
    for(int i = 1; i <= n; i ++)
    {
        scanf("%d", &a[i]);
        a[i + n] = a[i];  // 把环断开为链，然后复制一倍接在末尾
    }
    for(int i = 1; i <= n * 2; i ++)  a[i] = get_mod(a[i]);  // 计算前先对10取模 
	
    // 求前缀和
    for(int i = 1; i <= n * 2; i ++)  s[i] = s[i - 1] + a[i];

    memset(f, 0x3f, sizeof(f));  // 将最小值初始化为无穷大 
    memset(b, 0xaf, sizeof(b));  // 将最大值初始化为无穷小 

    for(int len = 1; len <= n; len++) // 外围枚举所有用到的区间长度，从1开始 
    {
        for(int l = 1; l + len - 1 < n * 2; l++) // 在每一个区间长度下，枚举左端点的位置 
        {
            int r = l + len - 1; // 区间长度已知，左端点已知，则可计算右端点 

            f[l][r][1] = b[l][r][1] = get_mod(s[r] - s[l - 1]);  // 在只划分1个区间的情况下，f 和 b 就是区间内的元素和 
            if(len == n && 1 == m)   // 如果当前区间长度正好是n，且m就是1，则更新待求的最大值和最小值 
            {
                min_ans = min(min_ans, f[l][r][m]);
                max_ans = max(max_ans, b[l][r][m]);
            }

            // 枚举 K
            for(int k = 2; k <= m; k++)
            {
                for(int j = l + k - 2; j <= r - 1; j++)  // j 为划分为 k 个区间的所有可能方案的最右侧划分点的范围：j ∈[L + K - 2, r - 1] 
                {   // “划分为 K 段的最小值”，是从“划分为 K - 1 段的最小值”转移而来。
                    f[l][r][k] = min(f[l][r][k], f[l][j][k - 1] * get_mod(s[r] - s[j]));                   
                    b[l][r][k] = max(b[l][r][k], b[l][j][k - 1] * get_mod(s[r] - s[j]));

                    if(len == n && k == m)  // 如果当前区间长度正好是n，且m就是k，则更新待求的最大值和最小值
                    {
                        min_ans = min(min_ans, f[l][r][m]);
                        max_ans = max(max_ans, b[l][r][m]);						
                    } 
                }            	
            } 
        }
    }
    
    printf("%d\n%d\n", min_ans, max_ans); 
    return 0;
}