0、前言

在上篇文章中，我们对什么是数字图像、以及数字图像的组成（离散的像素点）进行了讲解🔗【计算机视觉】数字图像处理基础知识：模拟和数字图像、采样量化、像素的基本关系、灰度直方图、图像的分类。

我们知道，数字图像其实就是像素点组成的二维矩阵。本节我们要讲的就是基于这个二维矩阵进行一些数学上的基本运算（本质就是就是矩阵的计算——线性代数），对图像进行处理，这些基本运算也是数字图像处理的基础和基本算法，本节我们将介绍这些基本算法。

分别有以下几类

• 点运算：以一副图像（一个二维矩阵）为处理对象，图像中的像素点（矩阵中的值）为处理单位，对图像中的每个像素点进行按一定函数关系的运算，得到一副新图像的处理过程。
• 代数运算：以两幅图像（两个二维矩阵）为处理对象，对两幅图像的对应像素之间进行加减乘除，得到一副输出图像。
• 逻辑运算：也是以两幅图像（两个二维矩阵）为处理对象，对两幅图像的对应像素之间进行逻辑运算，得到输出图像。
• 几何运算：是以一副图像为处理单位，对图像中的不同像素进行变换（改变像素之间的空间关系），从而实现处理后得到的图像进行了几何变换（翻转、镜像、平移等）。

Tips: 我们在进行下面的基本运算时，都是将像素值进行归一化到[0, 1]的取值范围的，方便变换和计算。在对应变换的时候也需要注意这点，避免产生误解。

一、点运算

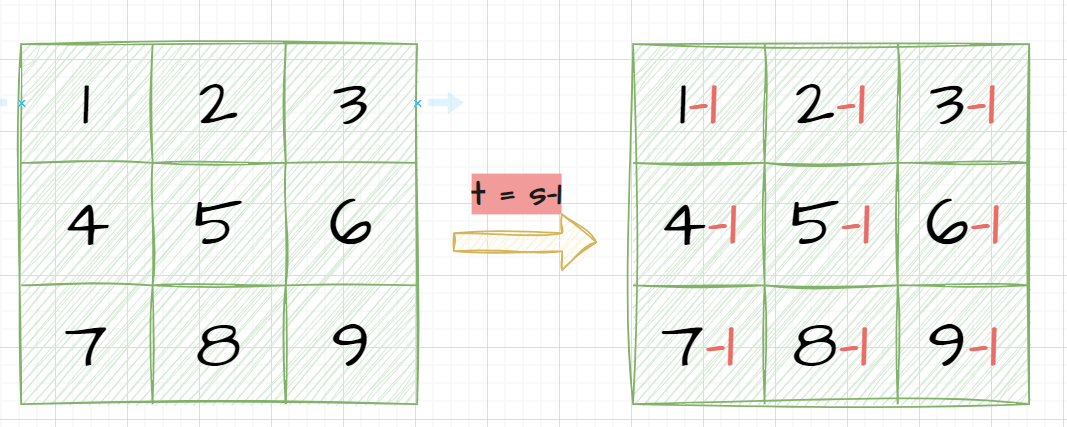
点运算是基于图像中每个像素点的像素值进行运算的图像处理方法。通过对输入图像的像素值和输入图像的像素值之间建立函数映射关系，实现“从像素到像素”的复制操作，输出图像中的每个像素值仅仅和输入图像中对应位置的像素值以及输入到输出像素之间的函数映射关系有关。

💐根据这个函数关系是否线性，我们可以把点运算分为两类：

• 线性点运算
• 非线性点运算

1.1：线性点运算

线性点运算是指输入图像的像素值和输出图像的像素值之间为线性函数关系：

$$O(x,y)=a\times I(x,y)+b$$

1. $a=1,b=0$，则$O(x,y)=I(x,y)$，输入图像和输出图像相同； $a=1,b\ne 0$，则输出图像整体的灰度值增加或减少，图像整体变得更两或更暗
2. $a>1$，则输出图像对比度增大（因为像素之间的灰度差也增大了a倍），输出图像整体显示效果较输入图像会更亮。
3. $0\le a<1$,则输出图像对比度减小（因为像素之间的灰度差也减小了a倍），输出图像整体显示效果较输入图像更暗。
4. $a<0$, 则灰度值翻转：原来暗的地方变亮，原来亮的地方变暗

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取你的照片
image_path = 'kitten.jpg'  # 替换成你的照片路径
image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)
image = image / 255.0  # 将图像归一化到 [0, 1] 范围

# 定义线性点运算函数
def linear_point_operation(image, a, b):
    return np.clip(a * image + b, 0, 1)

# 定义不同的参数
params = [
    (1, 0),   # 原图
    (1, 0.2), # 增加亮度
    (2, 0),   # 增加对比度
    (0.5, 0), # 减少对比度
    (-1, 1)   # 灰度翻转
]

# 创建子图
fig, axes = plt.subplots(1, 5, figsize=(15, 5))
axes = axes.ravel()

# 显示原图和处理后的图像
for ax, (a, b) in zip(axes, params):
    processed_image = linear_point_operation(image, a, b)
    ax.imshow(processed_image, cmap='gray')
    ax.set_title(f'a={a}, b={b}')
    ax.axis('off')

plt.tight_layout()
plt.show()

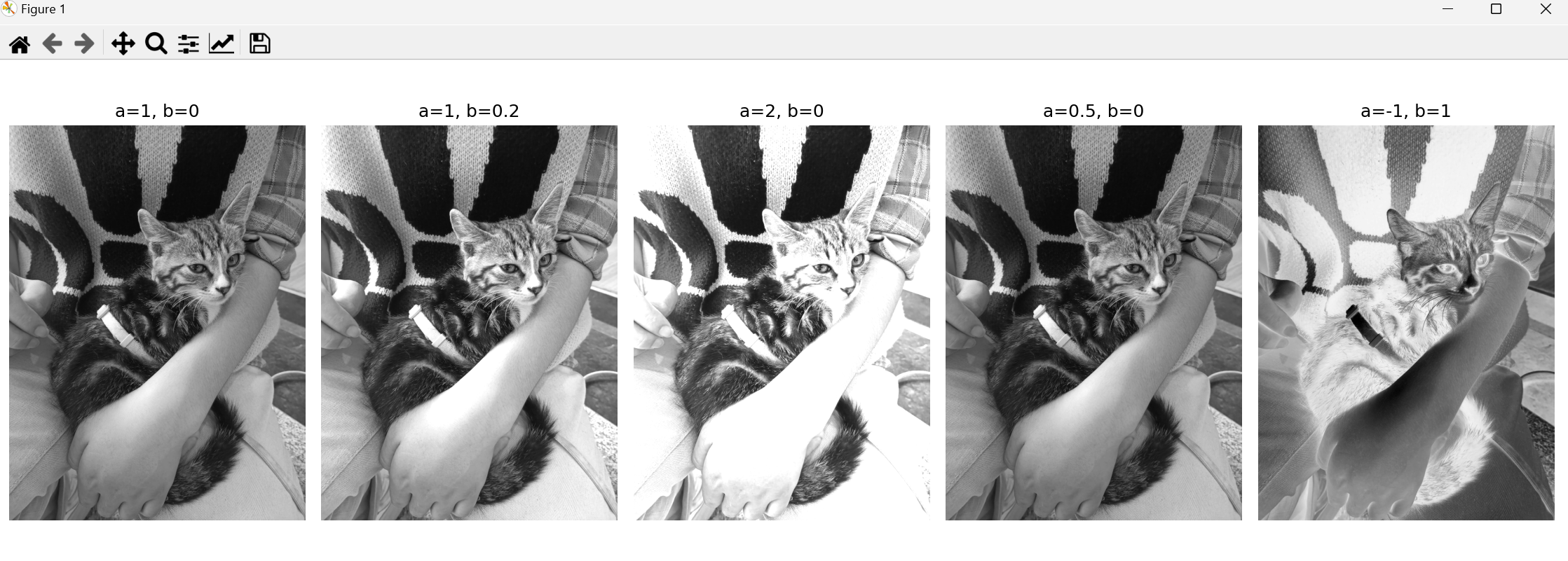
1.2：非线性点运算

非线性变换能更好模拟人眼对光强的感知特性，因为人眼对亮度的变化感知就是非线性的对数关系，它使图像看起来更加自然和舒适。

非线性点运算根据非线性函数的形式不同可以分为两类：

• 对数变换
• 指数变换

1.2.1：对数变换

表达式为：

$$O(x,y)=c{\log }_{}(1+I(x,y))$$
其中,c为尺度比例常数（变换范围/尺度大or小）

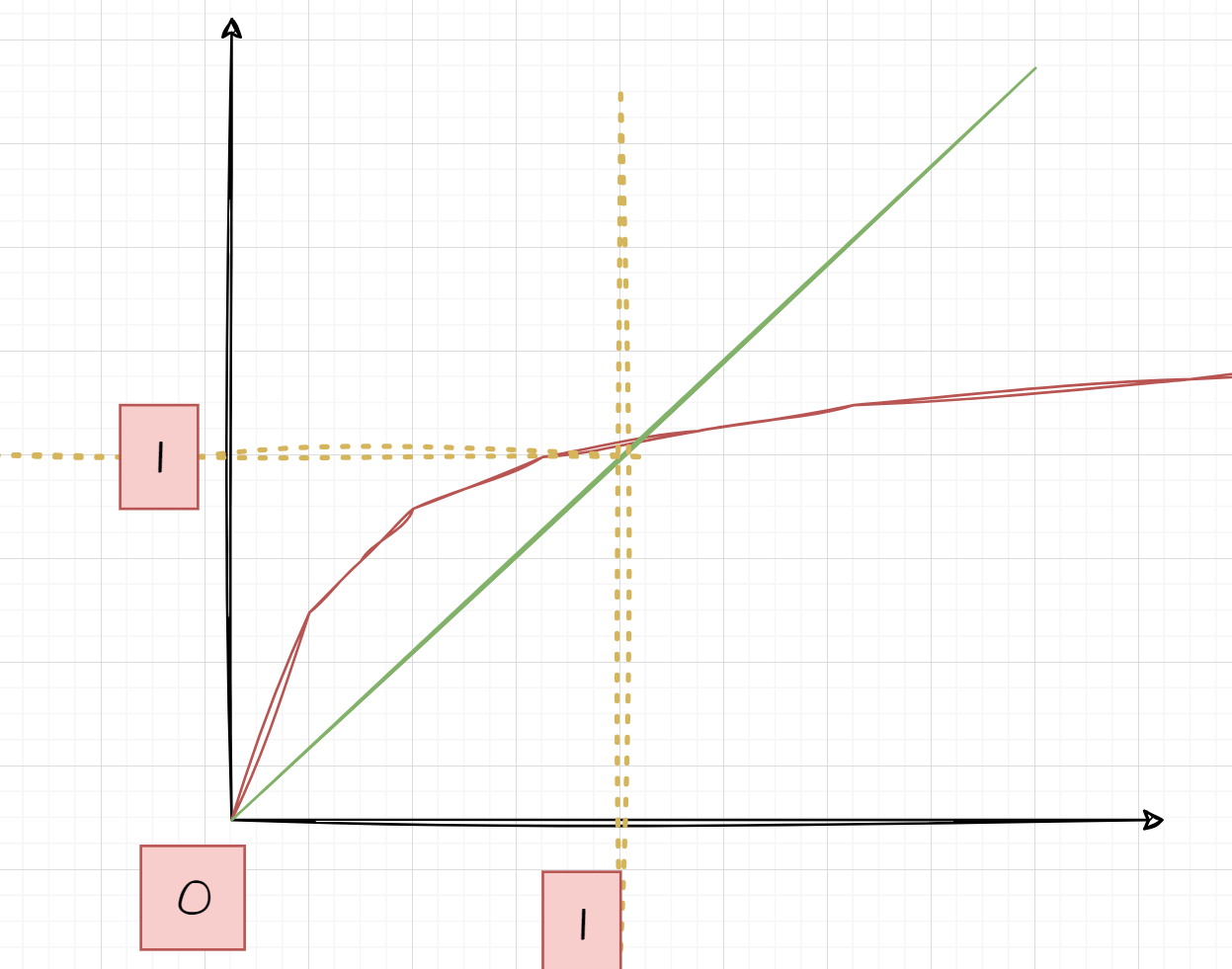
💁🏻‍♀️由对数变换曲线可以看到，在自变量小（原图像的灰度值底、暗）时，曲线斜率很高，因此因变量（输出图像）会增加的很大；在自变量大（原图像像素已经很亮）时，曲线斜率小，因变量（输出图像）增加的很小。

🪧对数变换的作用：

• 增强一副图像中较暗部分的细节，还原像素值动态范围高图像中被丢失的较暗的像素信息。（因为当像素的灰度值的动态扩展范围很高，但是设备的动态存储范围不满足，且图像像素值主要居于高像素值，则那些低像素值的信息不得不被丢弃，从而损失了大量暗部细节）。
• 使用对数变换，图像的动态范围被合理压缩（而不是由于设备原有限制而直接丢弃，且高值像素也不会过曝），从而可以清晰显示暗部信息。（eg: 前面博客里讲到的傅里叶变换得到的频谱，其动态范围可能宽达$0\sim 10^6$,直接显示频谱时，图像显示设备的动态范围往往不能满足要求，从而丢失大量暗部细节）。

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取你的照片
image_path = 'me.jpg'  # 替换成你的照片路径
image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)
image = image / 255.0  # 将图像归一化到 [0, 1] 范围

# 定义对数变换函数
def log_transform(image, c=1):
    return c * np.log(1 + image)

# 进行对数变换
c = 1
log_image = log_transform(image, c)

# 归一化到 [0, 1] 范围
log_image = cv2.normalize(log_image, None, 0, 1, cv2.NORM_MINMAX)

# 创建子图
fig, axes = plt.subplots(1, 2, figsize=(10, 5))
axes = axes.ravel()

# 显示原图和对数变换后的图像
axes[0].imshow(image, cmap='gray')
axes[0].set_title('Original Image')
axes[0].axis('off')

axes[1].imshow(log_image, cmap='gray')
axes[1].set_title('Log Transformed Image')
axes[1].axis('off')

plt.tight_layout()
plt.show()

个人觉得对数变换好在：

• 对于低光暗图像，它能极大的提升这些细节的可见性
• 而对于高像素值的高光照图像，它能在保证高光地方不会因为对数变换而变得过于曝光的前提下，还能增强暗部的细节。

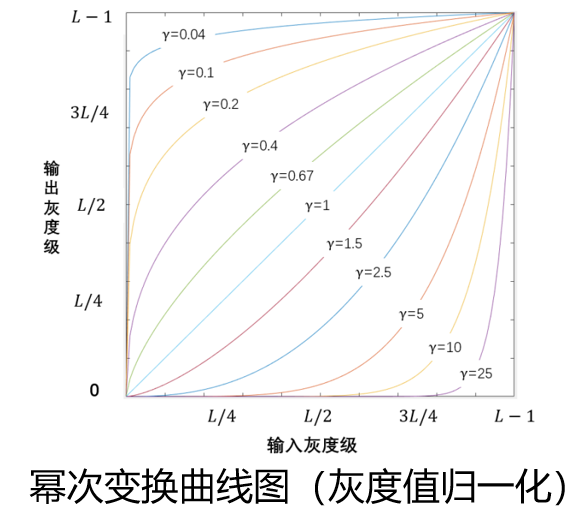
1.2.2：指数变换（幂次变换）

指数变换也叫幂次变换、伽马变换，其表达式为：

$$O(x,y)=cI(x,y{)}^{\gamma }$$

其中$c$和$\gamma$为正常数

指数变换比对数变换更加灵活，它能根据参数$c$和$\gamma$的不同取值，根据需求，选择是增强低灰度区域的对比度还是高灰度区域的对比度。

1. $0<\gamma <1$：效果和对数变换相似, 放大暗处细节；越大，效果越强
2. $\gamma >1$：放大亮处细节，压缩暗处细节；越大效果越强
3. $\gamma =1$：$O(x,y)=cI(x,y)$,相当于线性变换

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取你的照片
image_path = 'dim.png'  # 替换成你的照片路径
image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)
image = image / 255.0  # 将图像归一化到 [0, 1] 范围

# 定义幂次变换（伽马变换）函数
def gamma_transform(image, c, gamma):
    return c * np.power(image, gamma)

# 定义不同的参数
params = [
    (1, 0.5),  # 增强暗部细节
    (1, 1.0),  # 线性变换
    (1, 2.0),  # 增强亮部细节
    (0.5, 0.5),  # 增强暗部细节，降低亮度
    (2.0, 2.0)  # 增强亮部细节，提高亮度
]

# 创建子图
fig, axes = plt.subplots(2, 3, figsize=(15, 10))
axes = axes.ravel()

# 显示原图
axes[0].imshow(image, cmap='gray')
axes[0].set_title('Original Image')
axes[0].axis('off')

# 显示不同参数下的幂次变换后的图像
for ax, (c, gamma) in zip(axes[1:], params):
    transformed_image = gamma_transform(image, c, gamma)
    transformed_image = np.clip(transformed_image, 0, 1)  # 确保像素值在 [0, 1] 范围内
    ax.imshow(transformed_image, cmap='gray')
    ax.set_title(f'c={c}, γ={gamma}')
    ax.axis('off')

# 隐藏多余的子图框
for ax in axes[len(params) + 1:]:
    ax.axis('off')

plt.tight_layout()
plt.show()

二、代数运算

图像的代数运算是指将两幅或多幅图像通过对应像素之间加、减、乘、除的操作，得到输出图像的方法。

其实也就是矩阵运算：

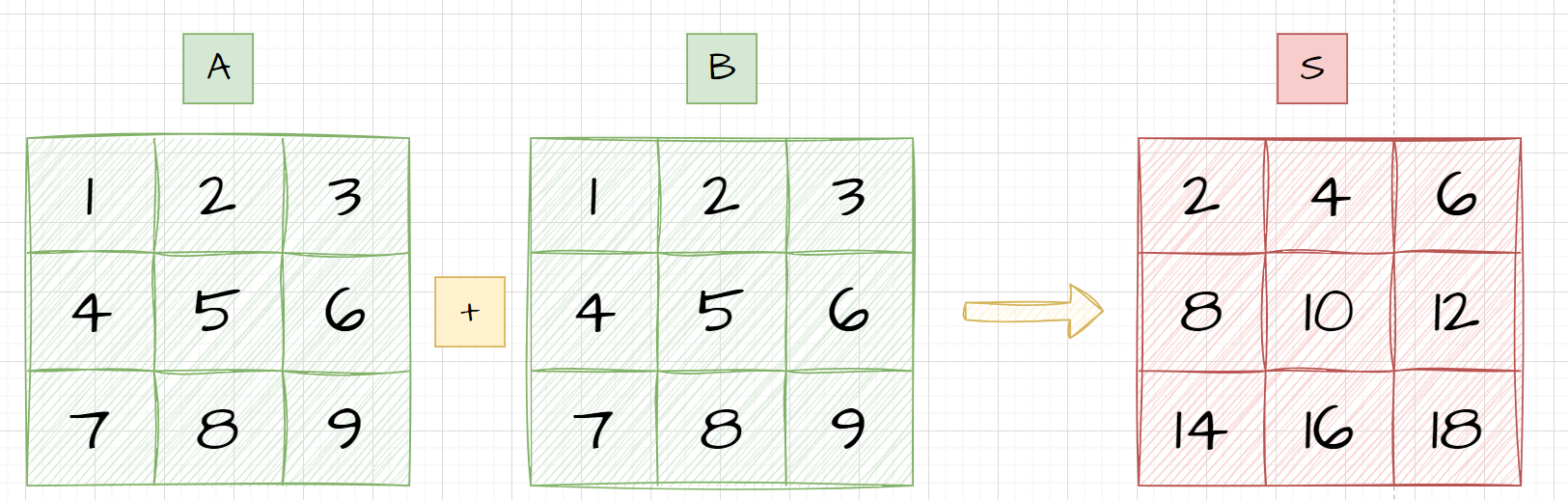
它们的表达式如下

1. 加$$S(x,y)=A(x,y)+B(x,y)$$
2. 减$$S(x,y)=A(x,y)-B(x,y)$$
3. 乘$$S(x,y)=A(x,y)\times B(x,y)$$
4. 除$$S(x,y)=A(x,y)÷B(x,y)$$

2.1：加法运算

💐应用1：图像叠加

将两幅图像进行加权混合的具体运算表达式如下：

$$OverlayImage(x,y)=\alpha \cdot Image1(x,y)+\beta \cdot Image2(x,y)+\gamma$$

其中：

• $OverlayImage(x,y)$ 是混合后的图像在位置 $(x,y)$的像素值。
• $Image1(x,y)$ 是第一幅图像在位置$(x,y)$ 的像素值。
• $Image2(x,y)$是第二幅图像在位置 $(x,y)$ 的像素值。
• $\alpha$ 是第一幅图像的权重（透明度）。
• $beta$ 是第二幅图像的权重（透明度），通常 (\beta = 1 - \alpha)。
• $\gamma$ 是一个可选的常数项，用于调整图像的亮度（通常为0）。

这个运算表达式通过 cv2.addWeighted 函数实现

1. 去噪：多幅图像相加求平均去除叠加性噪声。若图像中存在的各点噪声为互不相关的加性噪声，且均值为0，对同一景物连续摄取多幅图像，再对多幅图像相加取平均，消除噪声；

import cv2
import numpy as np
import matplotlib.pyplot as plt

def add_noise(image, mean=0, sigma=25):
    """添加高斯噪声到图像"""
    gauss = np.random.normal(mean, sigma, image.shape).astype('uint8')
    noisy_image = cv2.add(image, gauss)
    return noisy_image

def average_images(images):
    """对多幅图像进行叠加并求平均"""
    avg_image = np.mean(images, axis=0).astype('uint8')
    return avg_image

# 读取原始图像
image = cv2.imread('dog.jpg', cv2.IMREAD_GRAYSCALE)

# 添加噪声并生成多幅图像
num_images = 10
noisy_images = [add_noise(image) for _ in range(num_images)]

# 对多幅图像进行叠加并求平均
denoised_image = average_images(noisy_images)

# 显示原始图像、噪声图像和去噪后的图像
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
axes[0].imshow(image, cmap='gray')
axes[0].set_title('Original Image')
axes[0].axis('off')

axes[1].imshow(noisy_images[0], cmap='gray')
axes[1].set_title('Noisy Image')
axes[1].axis('off')

axes[2].imshow(denoised_image, cmap='gray')
axes[2].set_title('Denoised Image')
axes[2].axis('off')

plt.tight_layout()
plt.show()

2. 将一幅图像覆盖在另一幅图像上，通常使用透明度（alpha）值来控制叠加的效果。这种方法常用于创建视觉效果，如水印、徽标、特效等。

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取两幅图像
image1 = cv2.imread('dim.png')
image2 = cv2.imread('kitten.jpg')

# 调整图像大小相同
image2 = cv2.resize(image2, (image1.shape[1], image1.shape[0]))

# 设定权重
alpha = 0.3  # image1的权重
beta = 1 - alpha  # image2的权重
gamma = 0  # 常数项，通常为0

# 进行加权混合
overlay_image = cv2.addWeighted(image1, alpha, image2, beta, gamma)

# 显示混合后的图像
plt.imshow(cv2.cvtColor(overlay_image, cv2.COLOR_BGR2RGB))
plt.title('Overlay Image')
plt.axis('off')
plt.show()

代码解释

• alpha = 0.7：第一幅图像的权重（透明度）为 0.3。
• beta = 1 - alpha：第二幅图像的权重（透明度）为 0.7，确保两个权重值的总和为1。
• gamma = 0：常数项为0，不对图像亮度进行调整。
• cv2.addWeighted(image1, alpha, image2, beta, gamma)：将 image1 和 image2 按照指定的权重进行加权混合，生成叠加后的图像。
  

💐应用2：图像信息融合

图像融合的具体运算表达式与图像叠加的表达式类似，但通常图像融合的目的是为了结合多幅图像的信息，以提高图像的质量或增加图像的信息量。图像融合的运算表达式和图像叠加一样（只不过$\alpha$和$\beta$一般只会设置为0.5)，表示为：

$$FusedImage(x,y)=\alpha \cdot Image1(x,y)+\beta \cdot Image2(x,y)+\gamma$$

当然，图像融合在多个领域中有着广泛的应用，尤其是在提高图像质量和增加信息量方面。以下是几个具体的应用场景：

1. 医学图像处理
   在医学图像处理中，图像融合技术用于结合不同成像模式（如CT、MRI、PET等）的图像，以提供更全面的诊断信息。例如：

• CT和MRI图像融合：CT图像提供骨骼结构的详细信息，而MRI图像提供软组织的详细信息。通过融合这两种图像，可以获得更全面的解剖结构信息，有助于医生进行更准确的诊断和治疗计划。
• PET和MRI图像融合：PET图像显示代谢活动，而MRI图像显示解剖结构。融合这些图像可以帮助医生更好地理解肿瘤的代谢活动和其在解剖结构中的位置。

2. 遥感图像处理
   在遥感图像处理中，图像融合技术用于结合不同传感器获取的图像，以提高图像的空间分辨率和光谱信息。例如：

• 全色图像和多光谱图像融合：全色图像具有高空间分辨率，但缺乏光谱信息；多光谱图像具有丰富的光谱信息，但空间分辨率较低。通过融合这两种图像，可以获得既具有高空间分辨率又具有丰富光谱信息的图像，有助于地物分类、植被监测和环境监测等任务。
• 雷达图像和光学图像融合：雷达图像具有全天候、全天时的成像能力，而光学图像提供丰富的光谱信息。融合这些图像可以提高目标检测和识别的准确性。

3. 多光谱图像处理
   在多光谱图像处理中，图像融合技术用于结合不同波段的图像，以提高图像的光谱分辨率和信息量。例如：

• 红外图像和可见光图像融合：红外图像在夜间或恶劣天气条件下具有较好的成像能力，而可见光图像在良好的光照条件下提供丰富的细节信息。融合这些图像可以在各种环境条件下提供更清晰和详细的图像。
• 高光谱图像融合：高光谱图像包含大量波段的信息，通过融合不同波段的图像，可以提取更多的光谱特征，有助于精细的地物分类和目标识别。

4. 安防监控
   在安防监控领域，图像融合技术用于结合不同摄像头的图像，以提高监控系统的性能。例如：

• 红外摄像头和可见光摄像头融合：红外摄像头在夜间或低光照条件下具有较好的成像能力，而可见光摄像头在白天提供丰富的细节信息。通过融合这两种摄像头的图像，可以在全天候条件下提供高质量的监控图像，提高目标检测和识别的准确性。

5. 工业检测
   在工业检测领域，图像融合技术用于结合不同成像模式的图像，以提高检测精度和效率。例如：

• X射线图像和可见光图像融合：X射线图像可以穿透物体，显示其内部结构，而可见光图像提供表面细节信息。通过融合这些图像，可以更全面地检测产品的内部和外部缺陷，提高质量控制的准确性。

具体的图像融合方法
图像融合的方法有很多，常见的包括：

• 加权平均法：如前面提到的 cv2.addWeighted 方法，通过对图像像素值进行加权平均来实现融合。
• 小波变换法：利用小波变换将图像分解为不同频率的子带，对子带进行融合后再重建图像。
• 金字塔变换法：利用金字塔变换将图像分解为不同尺度的子图，对子图进行融合后再重建图像。
• 深度学习法：利用卷积神经网络等深度学习方法对图像进行特征提取和融合。

图像融合技术在各个领域中的应用极大地提高了图像处理的效果和效率，为科学研究、工业生产和日常生活带来了诸多便利。

💐应用3：图像增强

🚨:"图像增强"≠“数据增强”。前者是增强一副图像的特征，提高图像的可见性和识别效果；后者是因为训练模型时数据不够或需要鲁棒性而增加数据的数量。

通过将原始图像与增强图像（如边缘检测结果）相加，可以增强图像的某些特征，从而提高图像的可见性或识别效果。

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取图像
image = cv2.imread('kitten.jpg', cv2.IMREAD_GRAYSCALE)

# 进行边缘检测
edges = cv2.Canny(image, 100, 200)

# 将边缘图像与原始图像相加
enhanced_image = cv2.add(image, edges)

# 显示图像
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
axes[0].imshow(image, cmap='gray')
axes[0].set_title('Original Image')
axes[0].axis('off')

axes[1].imshow(edges, cmap='gray')
axes[1].set_title('Edges')
axes[1].axis('off')

axes[2].imshow(enhanced_image, cmap='gray')
axes[2].set_title('Enhanced Image')
axes[2].axis('off')

plt.tight_layout()
plt.show()

2.2：减法运算

图像的减法运算也称为差分方法，将两幅图像进行对应像素值相减可以用来检测图像的变化（缺陷检测）、物体的运动等。

💐应用1：运动检测

运动检测是通过对一个视频的连续帧相减，来判断是否有运动的物体（or外来人员检测）。

import cv2
import numpy as np

def motion_detection(video_path, window_size=(640, 480)):
    cap = cv2.VideoCapture(video_path)

    ret, frame1 = cap.read()
    if not ret:
        print("Failed to read video")
        return

    prvs = cv2.cvtColor(frame1, cv2.COLOR_BGR2GRAY)

    while cap.isOpened():
        ret, frame2 = cap.read()
        if not ret:
            break

        next = cv2.cvtColor(frame2, cv2.COLOR_BGR2GRAY)
        diff = cv2.absdiff(prvs, next)
        _, thresh = cv2.threshold(diff, 30, 255, cv2.THRESH_BINARY)

        # 调整窗口大小
        cv2.namedWindow('Original', cv2.WINDOW_NORMAL)
        cv2.resizeWindow('Original', window_size[0], window_size[1])
        cv2.imshow('Original', frame2)

        cv2.namedWindow('Motion Detection', cv2.WINDOW_NORMAL)
        cv2.resizeWindow('Motion Detection', window_size[0], window_size[1])
        cv2.imshow('Motion Detection', thresh)

        prvs = next

        if cv2.waitKey(30) & 0xFF == 27:
            break

    cap.release()
    cv2.destroyAllWindows()

if __name__ == "__main__":
    video_path = 'D:/CollegeStudy/AI/windElectProject/VS2019_cpp/data/video_good/test_video.mp4'
    window_size = (800, 600)  # 设置窗口大小
    motion_detection(video_path, window_size)

前一帧减去后一帧，再二值化，没有运动的地方结果为0，显示为黑色，运动的地方结果为1

💐应用2：背景减除：

通过从当前图像中减去背景图像，可以去除背景，仅保留前景，这对对象检测和跟踪中是否有用。

import cv2
import matplotlib.pyplot as plt

def background_subtraction(image_path, background_path):
    image = cv2.imread(image_path)
    background = cv2.imread(background_path)

    gray_image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
    gray_background = cv2.cvtColor(background, cv2.COLOR_BGR2GRAY)

    diff = cv2.absdiff(gray_background, gray_image)
    _, thresh = cv2.threshold(diff, 30, 255, cv2.THRESH_BINARY)

    # 将BGR图像转换为RGB图像以便使用matplotlib显示
    image_rgb = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
    background_rgb = cv2.cvtColor(background, cv2.COLOR_BGR2RGB)

    # 使用matplotlib显示图像
    plt.figure(figsize=(15, 5))

    plt.subplot(1, 3, 1)
    plt.title("Original Image")
    plt.imshow(image_rgb)
    plt.axis('off')

    plt.subplot(1, 3, 2)
    plt.title("Background Image")
    plt.imshow(background_rgb)
    plt.axis('off')

    plt.subplot(1, 3, 3)
    plt.title("Foreground (Processed Image)")
    plt.imshow(thresh, cmap='gray')
    plt.axis('off')

    plt.show()

if __name__ == "__main__":
    image_path = 'people.png'
    background_path = 'background.png'
    background_subtraction(image_path, background_path)

但是实际过程中我们可能一开始没有背景图像（已经有人在里面了），这个时候我们要用其他技术，取根据图片信息获取到背景：背景建模：在动态场景中，可以通过背景建模的方法来获取背景图像。背景建模通常利用多帧图像来估计背景，常见的方法包括高斯混合模型（GMM）等。

当然背景也不是一成不变，在某些应用中，可以通过实时更新背景的方法来获取背景图像。例如，在视频监控中，可以逐帧更新背景图像，以适应背景的缓慢变化。

以下是一个通过高斯混合模型（GMM）进行背景估计和实时更新背景的示例代码：

import cv2
import numpy as np
import matplotlib.pyplot as plt

def background_subtraction(video_path):
    cap = cv2.VideoCapture(video_path)

    # 创建背景减除对象
    fgbg = cv2.createBackgroundSubtractorMOG2(history=500, varThreshold=16, detectShadows=True)

    while cap.isOpened():
        ret, frame = cap.read()
        if not ret:
            break

        # 应用背景减除
        fgmask = fgbg.apply(frame)

        # 获取当前背景图像
        background = fgbg.getBackgroundImage()

        # 将BGR图像转换为RGB图像以便使用matplotlib显示
        frame_rgb = cv2.cvtColor(frame, cv2.COLOR_BGR2RGB)
        background_rgb = cv2.cvtColor(background, cv2.COLOR_BGR2RGB)

        # 使用matplotlib显示图像
        plt.figure(figsize=(15, 5))

        plt.subplot(1, 3, 1)
        plt.title("Original Frame")
        plt.imshow(frame_rgb)
        plt.axis('off')

        plt.subplot(1, 3, 2)
        plt.title("Background Image")
        plt.imshow(background_rgb)
        plt.axis('off')

        plt.subplot(1, 3, 3)
        plt.title("Foreground Mask")
        plt.imshow(fgmask, cmap='gray')
        plt.axis('off')

        plt.show()

        if cv2.waitKey(30) & 0xFF == 27:
            break

    cap.release()
    cv2.destroyAllWindows()

if __name__ == "__main__":
    video_path = 'test.mp4'
    background_subtraction(video_path)

💐应用3：缺陷（病变）检测

医学图像分析通过对比不同时间点的医学图像来检测病变或异常变化、目前使用图像减法检测PCB上的缺陷零件的方法被证明速度非常快。以下是一个简单的示例代码：

import cv2

def medical_image_analysis(image_path1, image_path2):
    image1 = cv2.imread(image_path1, cv2.IMREAD_GRAYSCALE)
    image2 = cv2.imread(image_path2, cv2.IMREAD_GRAYSCALE)

    diff = cv2.absdiff(image1, image2)
    _, thresh = cv2.threshold(diff, 30, 255, cv2.THRESH_BINARY)

    cv2.imshow('Medical Image 1', image1)
    cv2.imshow('Medical Image 2', image2)
    cv2.imshow('Change Detection', thresh)
    cv2.waitKey(0)
    cv2.destroyAllWindows()

if __name__ == "__main__":
    image_path1 = 'path/to/your/medical_image1.png'
    image_path2 = 'path/to/your/medical_image2.png'
    medical_image_analysis(image_path1, image_path2)

2.3：乘法运算：

将两副图像进行乘法运算，其实一般都是 掩膜(mask) 的作用：将一个图像作为遮罩/掩膜，与待处理图像对应像素位置相乘，从而只显示被遮罩or没有被遮罩部分内容，通过改变掩膜的形状可以对待处理图像中的信息进行处理。

将图像和某些滤波器逐像素相乘，也可以实现滤波作用。

比如在前面的傅里叶频谱处理过程中，高通or低通滤波就用到了和频谱大小一样的掩膜（mask)与原图像相乘，从而去掉高频or低频信息。

2.4：除法运算

将两个图像的像素点进行逐像素相除，它也能描述像素之间的差异，但不是像相减那样的绝对差异，它描述的是两幅图像对应像素值的变化比率。

通过像素值的变化比率，可以用于矫正成像设备的非线性影响：

原理解释
成像设备（如相机、扫描仪等）在捕捉图像时，可能会因为传感器的非均匀性、光学系统的不完美等原因，导致图像的亮度或颜色在空间上出现非线性变化。这种非线性影响会使得图像在不同位置的亮度或颜色表现不一致，即使实际场景是均匀的。
通过图像除法运算，可以将一幅受影响的图像与一幅理想情况下的参考图像进行相除，得到一个比率图像。这个比率图像反映了原始图像中每个像素相对于参考图像的变化比率，得到这个比率图像后对其进行合理处理，再乘以原图像相乘，从而消除了非线性影响。

校正过程的详细解释

1. 原始图像（Image1）：这是受成像设备非线性影响的图像。
2. 参考图像（Image2）：这幅图像应该反映理想情况下的图像，通常是在标准条件下拍摄的图像，或者经过某种处理得到的图像。

校正步骤

1. 获取参考图像：理想情况下，参考图像应该是没有非线性影响的图像。如果没有，可以通过多次拍摄取平均值，或者使用某种图像处理技术得到。

2. 图像相除：将原始图像逐像素除以参考图像，得到比率图像。

3. 比率图像处理： 使用 cv2.GaussianBlur 对比率图像进行高斯滤波，以减少噪声和不稳定因素。

4. 校正后的图像生成： 将比率图像与参考图像逐像素相乘，得到校正后的图像。

注意事项

• 参考图像的获取：参考图像应尽可能准确地反映成像设备在标准条件下的输出，可以通过多次扫描取平均值或使用标准化模具来获得。
• 图像配准：在进行图像相除之前，确保两幅图像在空间上严格对齐。可以使用图像配准算法（如基于特征点的配准或基于互信息的配准）来实现。
• 噪声处理：在实际应用中，图像可能包含噪声，除法运算可能会放大噪声，因此需要进行适当的噪声处理，如使用滤波器。

三、逻辑运算

逻辑运算主要针对的是二值图像，以像素为基础进行两幅或多幅图的操作。常见的逻辑运算：与、或、非、或非、与非、异或等。

import numpy as np
import cv2
import matplotlib.pyplot as plt

# 模拟两幅黑白图像的矩阵数据（0表示黑色，255表示白色）
image1 = np.array([[0, 255, 0],
                   [0, 255, 0],
                   [0, 255, 0]], dtype=np.uint8)

image2 = np.array([[0, 0, 0],
                   [255, 255, 255],
                   [0, 0, 0]], dtype=np.uint8)

# 逻辑与运算
and_image = cv2.bitwise_and(image1, image2)

# 逻辑或运算
or_image = cv2.bitwise_or(image1, image2)

# 逻辑非运算
not_image1 = cv2.bitwise_not(image1)
not_image2 = cv2.bitwise_not(image2)

# 逻辑异或运算
xor_image = cv2.bitwise_xor(image1, image2)

# 使用matplotlib显示图像
plt.figure(figsize=(15, 10))

plt.subplot(2, 3, 1)
plt.title("Original Image 1")
plt.imshow(image1, cmap='gray')
plt.axis('off')

plt.subplot(2, 3, 2)
plt.title("Original Image 2")
plt.imshow(image2, cmap='gray')
plt.axis('off')

plt.subplot(2, 3, 3)
plt.title("AND Operation")
plt.imshow(and_image, cmap='gray')
plt.axis('off')

plt.subplot(2, 3, 4)
plt.title("OR Operation")
plt.imshow(or_image, cmap='gray')
plt.axis('off')

plt.subplot(2, 3, 5)
plt.title("NOT Operation on Image 1")
plt.imshow(not_image1, cmap='gray')
plt.axis('off')

plt.subplot(2, 3, 6)
plt.title("XOR Operation")
plt.imshow(xor_image, cmap='gray')
plt.axis('off')

plt.show()

四、几何运算

又称之为几何变换，不同于上面几种只是改变相同位置处的灰度值，几何变换不改变灰度值，只改变该像素在输出图像中的位置。

基本的结合变换本质也是对体现这个二维矩阵进行变换，根据变换方法不同（即像素坐标映射方法的不同），可以分为以下几种：

4.1：平移

$$x_1=x_0+△x，y_1=y_0+△y$$

其中x0,y0是该像素点在原始图像中的位置，x1,y1是该像素点映射到输出图像上的位置。

用矩阵的形式表示为：
$$\left(\begin{array}{c}{x}_1\\ y_1\\ 1\end{array}\right)=\left(\begin{array}{ccc}1& 0& \Delta x\\ 0& 1& \Delta y\\ 0& 0& 1\end{array}\right)\left(\begin{array}{c}{x}_0\\ x_1\\ 1\end{array}\right)$$

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取图像
image = cv2.imread('dog.jpg')
image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)  # 转换颜色空间到RGB

# 平移距离
tx, ty = 100, 50

# 创建平移矩阵
translation_matrix = np.float32([[1, 0, tx], [0, 1, ty]])

# 应用平移
translated_image = cv2.warpAffine(image, translation_matrix, (image.shape[1], image.shape[0]))

# 可视化
plt.subplot(1, 2, 1)
plt.imshow(image)
plt.title('Original Image')
plt.subplot(1, 2, 2)
plt.imshow(translated_image)
plt.title('Translated Image')
plt.show()

4.2：镜像

镜像变换又称之为对称变换，分为水平对称（水平镜像）、垂直对称（垂直镜像）等多种变换。

设原始图像的宽为w，高为h:

• 水平镜像：以图像竖直中轴线为中心轴，将左右两部分像素点进行对换。

$$\left(\begin{array}{c}{x}_1\\ y_1\\ 1\end{array}\right)=\left(\begin{array}{ccc}-1& 0& w\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)\left(\begin{array}{c}{x}_0\\ x_1\\ 1\end{array}\right)$$

• 竖直镜像：以图像水平中轴线为中心轴，将上下两部分像素点进行兑换。

$$\left(\begin{array}{c}{x}_1\\ y_1\\ 1\end{array}\right)=\left(\begin{array}{ccc}1& 0& 0\\ 0& -1& h\\ 0& 0& 1\end{array}\right)\left(\begin{array}{c}{x}_0\\ x_1\\ 1\end{array}\right)$$

import cv2
import matplotlib.pyplot as plt

# 加载图像并转换颜色通道顺序，以便正确显示
image = cv2.imread('me.jpg')  # 替换为你的图像路径
image_rgb = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)

# 水平镜像
flipped_horizontally = cv2.flip(image_rgb, 1)

# 垂直镜像
flipped_vertically = cv2.flip(image_rgb, 0)

# 设置绘图
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
axes[0].imshow(image_rgb)
axes[0].set_title("Original Image")
axes[0].axis('off')

axes[1].imshow(flipped_horizontally)
axes[1].set_title("Horizontally Flipped")
axes[1].axis('off')

axes[2].imshow(flipped_vertically)
axes[2].set_title("Vertically Flipped")
axes[2].axis('off')

# 显示结果
plt.tight_layout()
plt.show()

4.3：旋转

旋转变换通常是以图像的中心为圆心，将像素点绕着这个圆心进行旋转一定角度。

为了描述这种旋转关系，我们先把在笛卡尔系下的坐标转换成极坐标表示：
$$\{\begin{array}{c}{x}_0=r\cos \alpha \\ y_0=r\sin \alpha \end{array}$$

当我们逆时针旋转β角度后，得到新坐标为：
$$\{\begin{array}{c}x=r\cos (\alpha -\beta )=r\cos \alpha \cos \beta +r\sin \alpha \sin \beta \\ y=r\sin (\alpha -\beta )=r\sin \alpha \cos \beta -r\cos \alpha \sin \beta \end{array}$$

将x0,y0带入：
$$\{\begin{array}{c}x=x_0\cos \beta +y_0\sin \beta \\ y=-x_0\sin \beta +y_0\cos \beta \end{array}$$

用矩阵表示为：

$$\left(\begin{array}{c}{x}_1\\ y_1\\ 1\end{array}\right)=\left(\begin{array}{ccc}\cos \beta & \sin \beta & 0\\ -\sin \beta & \cos \beta & 0\\ 0& 0& 1\end{array}\right)\left(\begin{array}{c}{x}_0\\ x_1\\ 1\end{array}\right)$$

import cv2
import matplotlib.pyplot as plt
import numpy as np

# 读取图像
image = cv2.imread('me.jpg')  # 替换为你的图像路径
image_rgb = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)  # 将BGR转换为RGB

# 获取图像的尺寸及中心点坐标
(h, w) = image.shape[:2]
(cx, cy) = (w // 2, h // 2)

# 设置旋转角度
angle = 45  # 旋转45度

# 获取旋转矩阵
M = cv2.getRotationMatrix2D((cx, cy), angle, 1.0)  # 中心点，旋转角度，缩放因数

# 执行旋转
rotated_image = cv2.warpAffine(image_rgb, M, (w, h))

# 可视化原始图像与旋转后的图像
plt.subplot(1, 2, 1)
plt.imshow(image_rgb)
plt.title('Original Image')
plt.axis('off')

plt.subplot(1, 2, 2)
plt.imshow(rotated_image)
plt.title('Rotated Image')
plt.axis('off')

plt.tight_layout()
plt.show()

在OpenCV的cv2.getRotationMatrix2D函数中，如果你提供一个正角度，图像将会沿着原点顺时针旋转。

4.4：缩放

图像缩放指的是改变图像的大小尺寸，这包括：放大、缩小。无论是在放大还是缩小的过程中。

缩放和前面三种几何运算不太一样，在于图像所方法不仅仅是图像位置的简单重新映射，因为图像尺寸的改变，必然带来新像素的产生和原有像素的合并，所以新图像中像素值需要通过插值算法来确定，这是一种由后往前的过程。

插值算法决定了新像素值的生成（不只是多出来的那些，而是整个输出图像的像素值），不同插值方法对图像的质量和细节产生不同的影响。

放大图像

当你放大一幅图像时，就会有新的像素点添加到图像中。这些新的像素点并没有直接对应于原始图像中的实际像素值。因此，需要通过插值的方式来估计这些新像素点的颜色值。常见的插值方法包括：

• 最近邻插值：选择最近的像素值作为新像素点的值，这种方式是最简单但可能导致锯齿状的效果。

  最近邻插值方法中的“最近”，是指在原始图像中距离新像素位置欧几里得距离最近的原始像素点的值被直接用作新像素点的值。换句话说，对于缩放后图像中的每一个新像素位置，算法都会在原始图像中寻找最接近这个新位置（在原始尺度上）的原始像素点(哪个像素点经过放缩变换后离它最近），并将该原始像素点的值直接赋给新像素点。

  假设有一个原始图像需要放大，当你需要计算新图像中某个像素点的值时：
  首先，你将这个新像素点的位置映射回原始图像的尺度。
  然后，寻找与映射位置最接近的原始像素点。
  最后，直接使用这个最近原始像素点的值作为新像素点的值。

• 双线性插值：基于周围4个像素点的线性插值，能够得到更加平滑的效果。

  step1:确定周围的四个像素：在缩放过程中，新像素位置会落在原始像素构成的网格中的某些位置。为了计算新像素的值，我们需要找到原始图像中最接近新像素位置的四个像素。
  step2:计算距离权重：基于新像素位置与这四个像素位置在x和y轴方向上的距离，计算每个像素对新像素值的贡献权重。距离越近，权重越大。
  step3:加权平均：用找到的四个像素值和对应的权重，计算加权平均值，这个值即为新像素的值。

• 双三次插值（立方插值）：基于周围16个像素点的更复杂的插值，能够得到更平滑的边缘。

缩小图像

当缩小图像时，原始图像中的多个像素值会映射到新图像中的单个像素点上。因此必须采取某种策略来决定新像素点的值。常见的方法包括：

• 区域插值：通过结合原图像中缩放区域内所有像素值的平均值来确定新像素点的值。
• 毛玻璃插值：基于统计学方法（如平均值或中值），结合原图像中像素的随机样本来决定新像素点的值。

总之，无论是放大还是缩小图像，都需要通过某种方式来填充新的像素点或合并多个像素点，而这正是插值发挥作用的地方。插值方法的选择会直接影响图像缩放后的质量，因此在缩放图像时应当考虑所使用的插值方法。在OpenCV中，cv2.resize()函数让你可以指定使用的插值方法，以达到最佳的缩放效果。

import cv2
import matplotlib.pyplot as plt
import math

# 加载图像，并转换颜色为RGB
image = cv2.imread('me.jpg')  # 替换为你的图像路径
image_rgb = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)

# 设置不同的缩放因子
scales = [0.25, 0.5, 0.75, 1.25, 1.5]  # 将分别缩放25%, 50%, 75%, 125%, 和 150%

# 确定subplot的行数和列数
rows = 2
cols = 3

# 创建subplot
fig, axes = plt.subplots(rows, cols, figsize=(20, 10))

# 将原始图像和缩放后的图像放入list,双线性插值方法
images = [image_rgb] + [cv2.resize(image_rgb, None, fx=scale, fy=scale, interpolation=cv2.INTER_LINEAR) for scale in scales]
titles = ['Original Image'] + [f'Scale {scale*100}%' for scale in scales]

# 填充每个subplot
for i, ax in enumerate(axes.flat):
    if i < len(images):
        ax.imshow(images[i])
        ax.set_title(titles[i])
    ax.axis('off')

plt.tight_layout()
plt.show()