例题一

解法(贪⼼):
贪⼼策略:
由于只能交易⼀次,所以对于某⼀个位置
i
,要想获得最⼤利润,仅需知道前⾯所有元素的最⼩ 值。然后在最⼩值的位置「买⼊」股票,在当前位置「卖出」股票即可。

例题二

解法(贪⼼):
贪⼼策略:
由于可以进⾏⽆限次交易,所以只要是⼀个「上升区域」,我们就把利润拿到⼿就好了。

例题三

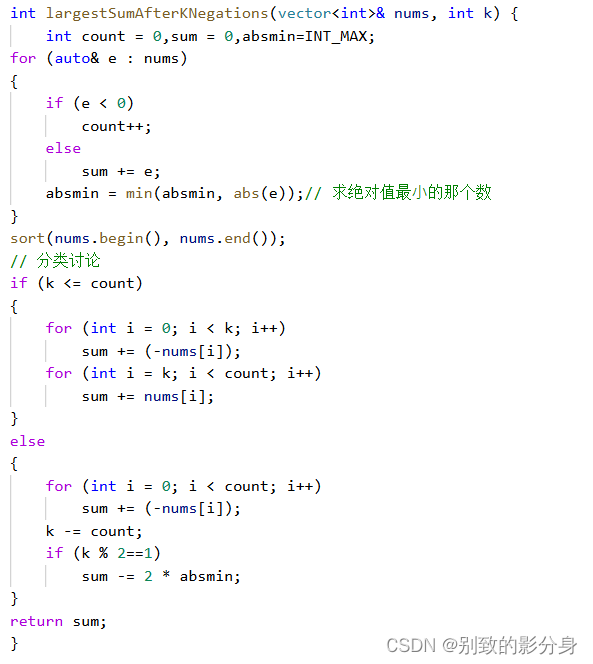
解法(贪⼼):
贪⼼策略:
分情况讨论,设整个数组中负数的个数为
m
个:
a.
m > k
:把前
k
⼩负数,全部变成正数;
b.
m == k
:把所有的负数全部转化成正数;
c.
m < k
:
i.
先把所有的负数变成正数;
ii.
然后根据
k - m
的奇偶分情况讨论:
1.
如果是偶数,直接忽略;
2.
如果是奇数,挑选当前数组中最⼩的数,变成负数
例题四

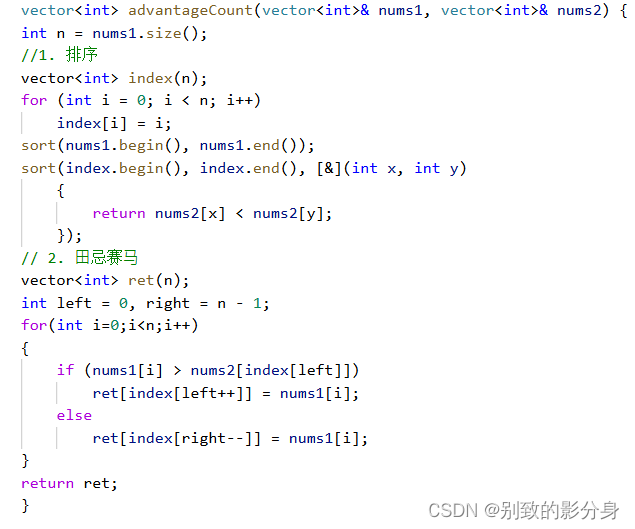
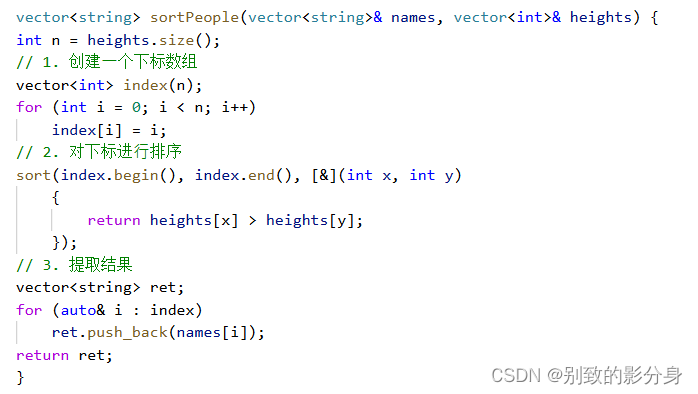
解法(通过排序 ''索引'' 的⽅式):
算法思路:
我们不能直接按照
i
位置对应的
heights
来排序,因为排序过程是会移动元素的,但是names 内的元素是不会移动的。由题意可知,names
数组和
heights
数组的下标是⼀⼀对应的,因此我们可以重新创建出来⼀个下标数组,将这个下标数组按照 heights[i]
的⼤⼩排序。那么,当下标数组排完序之后,⾥⾯的顺序就相当于 heights
这个数组排完序之后的下标。之后通过排序后的下标,依次找到原来的 name
,完成对名字的排序。
例题五

解法(贪⼼):
讲⼀下⽥忌赛⻢背后包含的博弈论和贪⼼策略:
⽥忌赛⻢没听过的⾃⾏百度,这⾥讲⼀下⽥忌赛⻢背后的博弈决策,从三匹⻢拓展到
n
匹⻢之间博弈的最优策略。
⽥忌:下等⻢ 中等⻢ 上等⻢
⻬王:下等⻢ 中等⻢ 上等⻢
a.
⽥忌的下等⻢
pk
不过⻬王的下等⻢,因此把这匹⻢丢去消耗⼀个⻬王的最强战⻢!
b.
接下来选择中等⻢
pk
⻬王的下等⻢,勉强获胜;
c.
最后⽤上等⻢
pk
⻬王的中等⻢,勉强获胜。
由此,我们可以得出⼀个最优的决策⽅式:
a.
当⼰⽅此时最差的⽐不过对⾯最差的时候,让我⽅最差的去处理掉对⾯最好的(反正要输,不如去拖掉对⾯⼀个最强的);
b.
当⼰⽅此时最差的能⽐得上对⾯最差的时候,就让两者⽐对下去(最差的都能获胜,为什么要输呢)。每次决策,都会使我⽅处于优势。