数据结构复习指导之外部排序

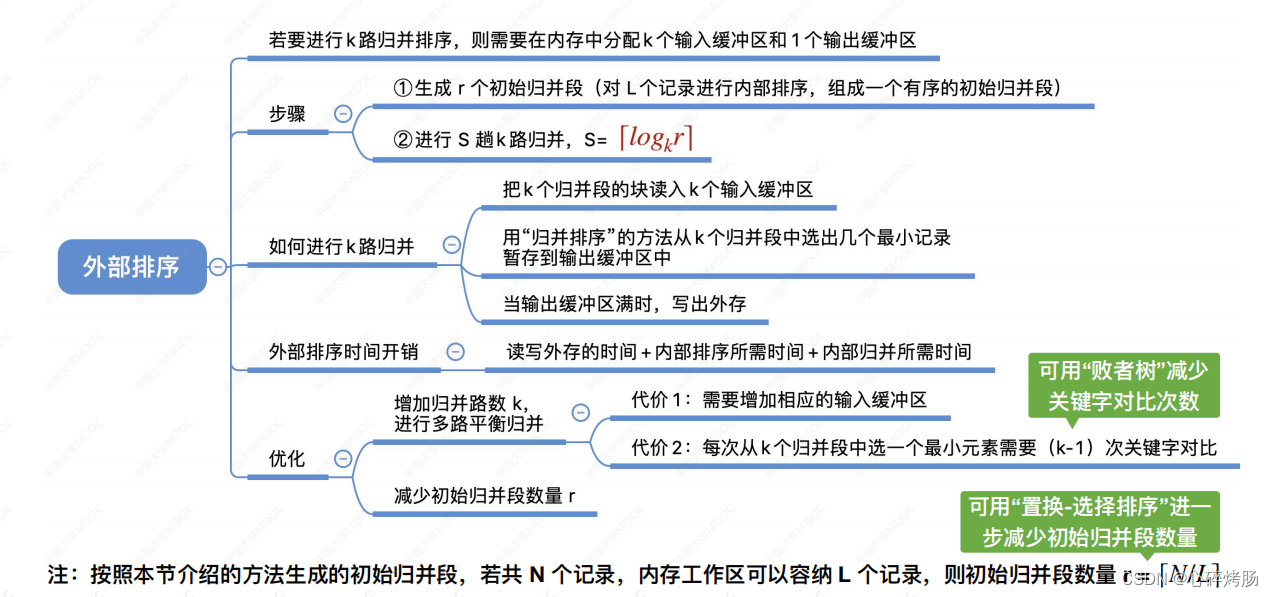
外部排序

复习提示

1.外部排序的基本概念

2.外部排序的方法

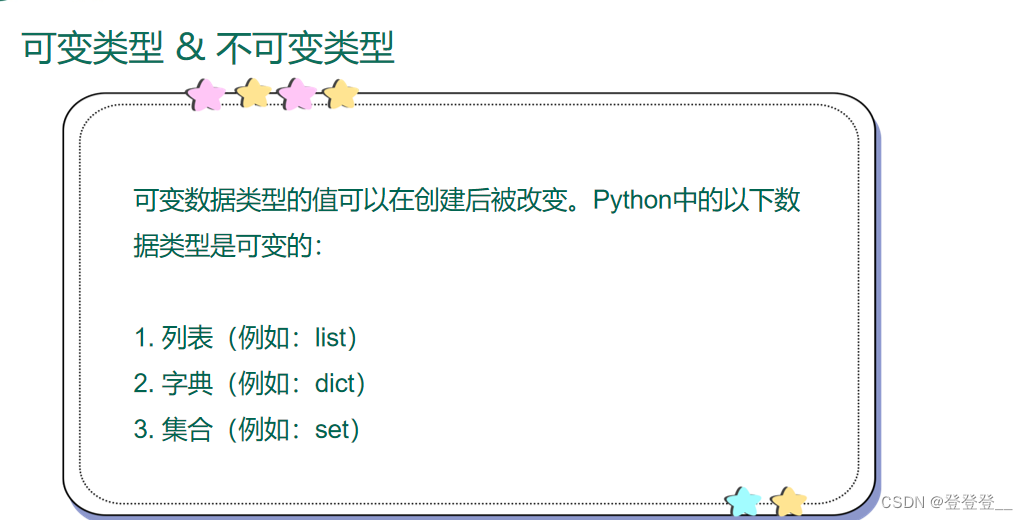
2.1对大文件排序时使用的排序算法（2016）

3.多路平衡归并与败者树

4.置换-选择排序（生成初始归并段）

4.1置换-选择排序生成初始归并段的实例(2023)

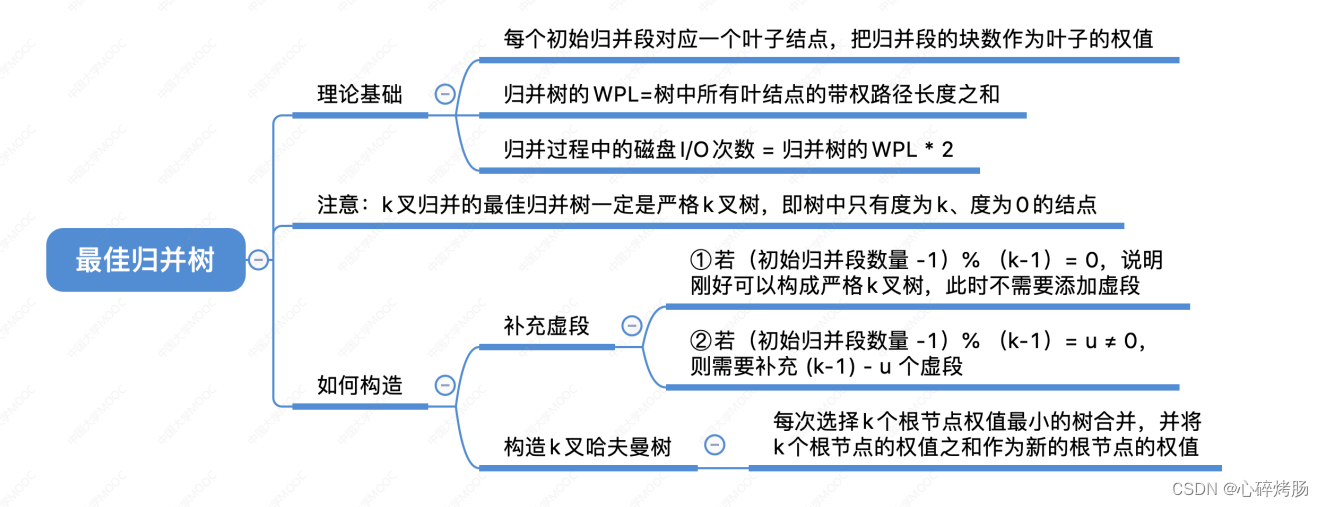
5.最佳归并树

5.1构造三叉哈夫曼树及相关的分析和计算(2013)

5.2实现最佳归并时需补充的虚段数量的分析(2019)

知识回顾

外部排序

复习提示

外部排序可能会考查相关概念、方法和排序过程，外部排序的算法比较复杂，不会在算法设计上进行考查。

本节的主要内容有:

① 外部排序指的是大文件的排序，即待排序的记录存储在外存中，待排序的文件无法一次性装入内存，需要在内存和外存之间进行多次数据交换，以达到排序整个文件的目的。

② 为减少平衡归并中外存读/写次数所采取的方法：增大归并路数和减少归并段个数。

③ 利用败者树增大归并路数。

④ 利用置换-选择排序增大归并段长度来减少归并段个数。

⑤ 由长度不等的归并段进行多路平衡归并，需要构造最佳归并树。

1.外部排序的基本概念

前面介绍过的排序算法都是在内存中进行的(称为内部排序)。

而在许多应用中，经常需要对大文件进行排序，因为文件中的记录很多，无法将整个文件复制进内存中进行排序。

因此，需要将待排序的记录存储在外存上，排序时再把数据一部分一部分地调入内存进行排序，在排序过程中需要多次进行内存和外存之间的交换。

这种排序算法就称为外部排序。

2.外部排序的方法

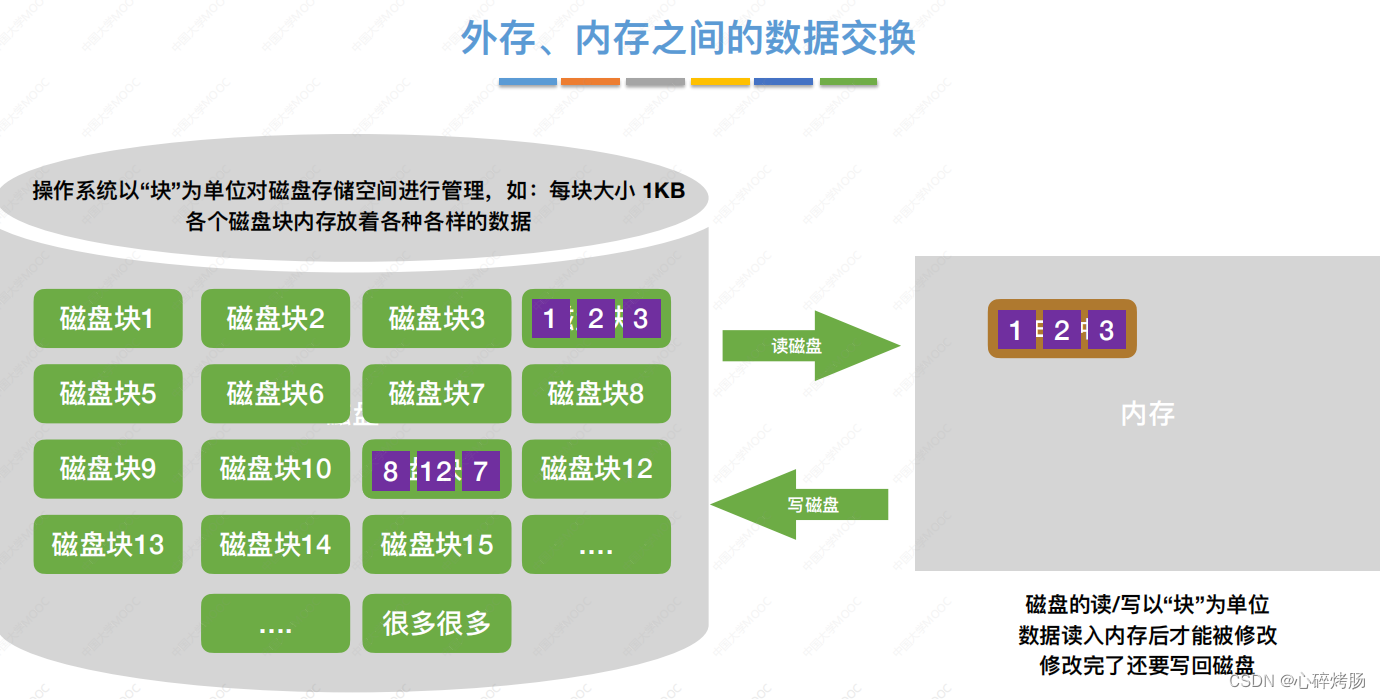
文件通常是按块存储在磁盘上的,操作系统也是按块对磁盘上的信息进行读/写的。

因为磁盘读/写的机械动作所需的时间远远超过在内存中进行运算的时间(相比而言可以忽略不计)，

因此在外部排序过程中的时间代价主要考虑访问磁盘的次数，即I/O次数。

2.1对大文件排序时使用的排序算法（2016）

外部排序通常采用归并排序算法。它包括两个阶段：

① 根据内存缓冲区大小，将外存上的文件分成若干长度为 L 的子文件，依次读入内存并利用内部排序算法对它们进行排序，并将排序后得到的有序子文件重新写回外存，称这些有序子文件为归并段或顺串；
② 对这些归并段进行逐趟归并，使归并段(有序子文件)逐渐由小到大，直至得到整个有序文件为止。

例如，一个含有 2000个记录的文件，每个磁盘块可容纳 125 个记录，首先通过8次内部排序得到 8个初始归并段 R1~R8，每段都含 250 条记录。

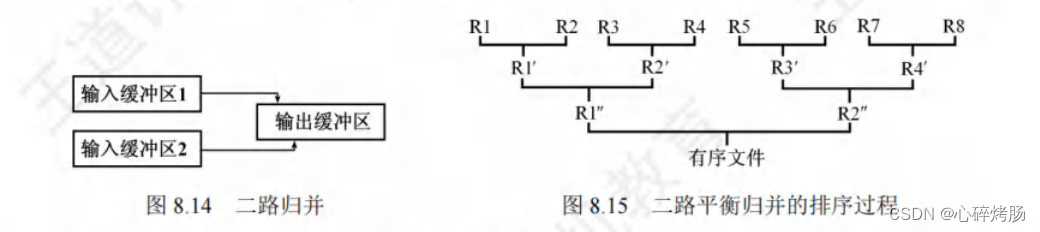
然后对该文件做如图 8.15 所示的两两归并，直至得到一个有序文件。

可以把内存工作区等分为三个缓冲区，如图8.14所示，其中的两个为输入缓冲区，一个为输出缓冲区。

首先，从两个输入归并段R1和 R2 中分别读入一个块，放在输入缓冲区1和输入缓冲区2中。

然后，在内存中进行二路归并，归并后的对象顺序存放在输出缓冲区中。

若输出缓冲区中对象存满，则将其顺序写到输出归并段(R1')中，再清空输出缓冲区，继续存放归并后的对象。

若某个输入缓冲区中的对象取空，则从对应的输入归并段中再读取下一块，继续参加归并。

如此继续，直到两个输入归并段中的对象全部读入内存并都归并完成为止。

当 R1 和 R2 归并完后，再归并 R3 和 R4、R5 和 R6、最后归并 R7和 R8，这是一趟归并。

再把上趟的结果 R1'和 R2'、R3'和 R4'两两归并，这又是一趟归并。

最后把 R1"和 R2"两个归并段归并，得到最终的有序文件，一共进行了3趟归并。

在外部排序中实现两两归并时，由于不可能将两个有序段及归并结果段同时存放在内存中，因此需要不停地将数据读出、写入磁盘，而这会耗费大量的时间。

一般情况下：

外部排序的总时间 = 内部排序的时间 + 外存信息读/写的时间 + 内部归并的时间

显然，外存信息读/写的时间远大于内部排序和内部归并的时间，因此应着力减少 I/O 次数。

由于外存信息的读/写是以“磁盘块”为单位的，因此可知每趟归并需进行 16 次读和 16 次写，3趟归并加上内部排序时所需进行的读/写，使得总共需进行 32x3 +32=128 次读/写。

若改用 4 路归并排序，则只需2趟归并，外部排序时的总读/写次数便减至 32x2+32=96。

因此，增大归并路数，可减少归并趟数，进而减少总的磁盘 I/O 次数，如图 8.16 所示。

一般地，对 r 个初始归并段，做 k 路平衡归并(即每趟将 k 个或 k 个以下的有序子文件归并成一个有序子文件)。

第一趟可将 r 个初始归并段归并为 $\left \lceil r/k \right \rceil$ 个归并段，以后每趟归并将 m 个归并段归并成 $\left \lceil m/k \right \rceil$ 个归并段，直至最后形成一个大的归并段为止。

树的高度-1= $\left \lceil log_kr \right \rceil$ = 归并趟数S。

可见，只要增大归并路数k，或减少初始归并段个数r，都能减少归并趟数 S，进而减少读/写磁盘的次数，达到提高外部排序速度的目的。

3.多路平衡归并与败者树

增加归并路数 k 能减少归并趟数 S，进而减少 I/O 次数。

然而，增加归并路数 k 时，内部归并的时间将增加。

做内部归并时,在 k 个元素中选择关键字最小的元素需要k-1次比较。

每趟归并 n 个元素需要做 (n-1)(k-1) 次比较，S趟归并总共需要的比较次数为

$S(n-1)(k-1)=\left \lceil log_kr \right \rceil(n-1)(k-1)=$ $\left \lceil log_2r \right \rceil(n-1)(k-1)/\left \lceil log_2k \right \rceil$

式中， $(k-1)/\left \lceil log_2k \right \rceil$ 随 k 增长而增长，因此内部归并时间亦随 k 的增长而增长。

这将抵消因增大 k 而减少外存访问次数所得到的效益。因此，不能使用普通的内部归并排序算法。

为了使内部归并不受 k 的增大的影响，引入了败者树。

败者树是树形选择排序的一种变体，可视为一棵完全二叉树。

k 个叶结点分别存放 k 个归并段在归并过程中当前参加比较的元素，内部结点用来记忆左右子树中的“失败者”，而让胜利者往上继续进行比较，一直到根结点。

若比较两个数，大的为失败者、小的为胜利者，则根结点指向的数为最小数。

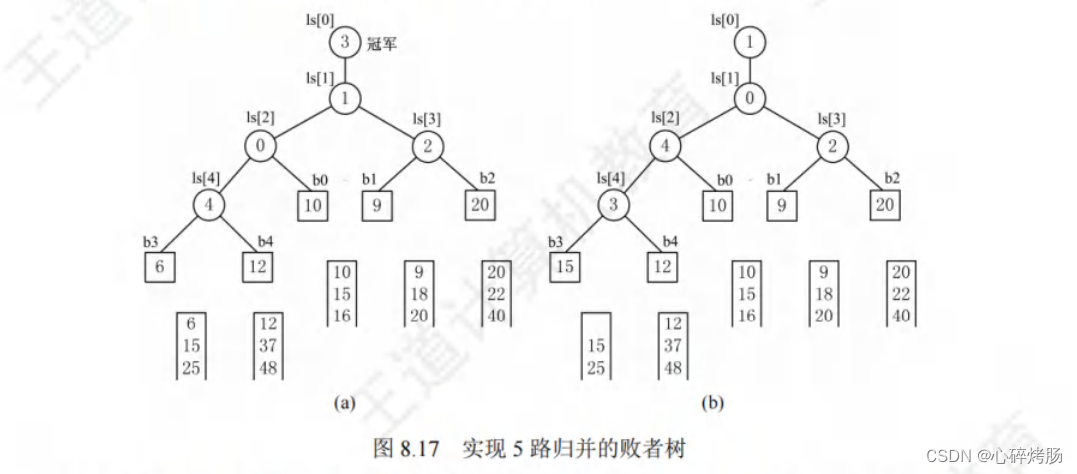
如图 8.17(a) 所示，

b3 与 b4 比较，b4 是败者，将段号 4 写入父结点 ls[4]（l为小写的L，并非大写的i，下面同理）。
b1 与 b2 比较，b2 是败者，将段号 2 写入 ls[3]。
b3 与 b4的胜者 b3 与 b0 比较，b0 是败者,，将段号0写入 Is[2]。
最后两个胜者 b3 与 b1 比较，b1是败者，将段号1写入Is[1]。
而将胜者b3 的段号3写入 ls[0] 此时，根结点 Is[0] 所指的段的关键字最小。

对于k路归并，初始构造败者树需要k-1次比较。

b3 中的 6 输出后，将下一关键字填入 b3，继续比较。

因为 k 路归并的败者树深度为 $\left \lceil log_2k \right \rceil+1$ ，所以从 k 个记录中选择最小关键字，仅需进行 $\left \lceil log_2k \right \rceil$ 次比较。

因此总的比较次数约为

$S(n-1)\left \lceil log_2k \right \rceil=\left \lceil log_kr \right \rceil(n-1)\left \lceil log_2k \right \rceil=(n-1)\left \lceil log_2r \right \rceil$

可见，使用败者树后，内部归并的比较次数与 k 无关了。

因此，只要内存空间允许，增大归并路数 k 将有效地减少归并树的高度，从而减少 I/O 次数，提高外部排序的速度。

值得说明的是，归并路数 k 并不是越大越好。

归并路数 k 增大时，相应地需要增加输入缓冲区的个数。

若可供使用的内存空间不变，势必要减少每个输入缓冲区的容量，使得内存、外存交换数据的次数增大。

当k值过大时，虽然归并趟数会减少，但读/写外存的次数仍会增加。

4.置换-选择排序（生成初始归并段）

从《外部排序的方法》节的讨论可知，减少初始归并段个数，也可以减少归并趟数 S。

若总的记录个数为n，每个归并段的长度为 l（此l为小写的L，并非大写的i），则归并段的个数 $r=\left \lceil n/l \right \rceil$ 。

采用内部排序算法得到的各个初始归并段长度都相同(除最后一段外)，它依赖于内部排序时可用内存工作区的大小。

因此，必须探索新的方法，用来产生更长的初始归并段，这就是本节要介绍的置换-选择算法。

4.1置换-选择排序生成初始归并段的实例(2023)

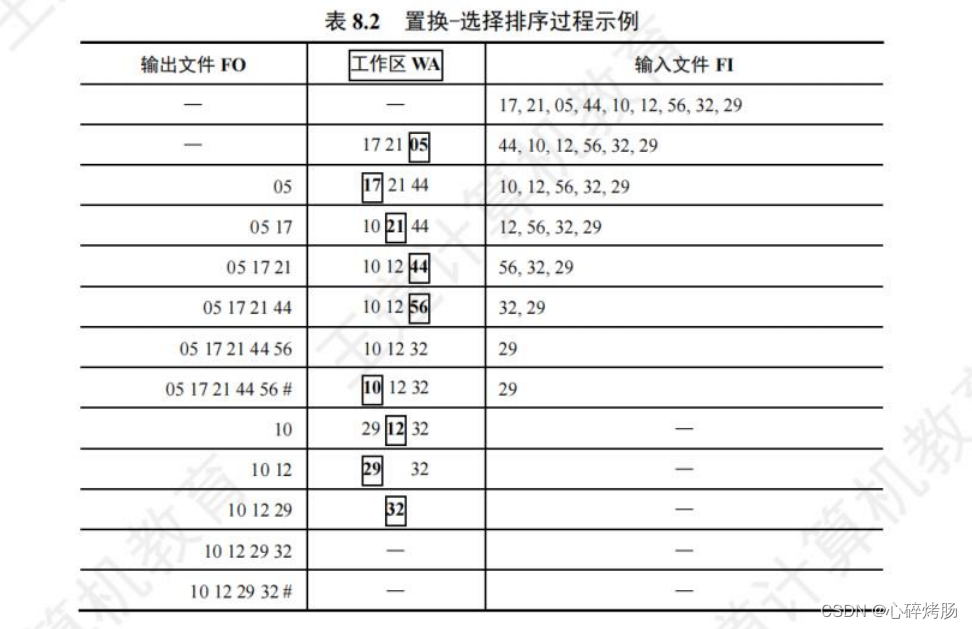
设初始待排文件为FI（此I为大写的i，非小写的L），初始归并段输出文件为FO，内存工作区为 WA，FO 和 WA 的初始状态为空，WA可容纳 w 个记录。

置换-选择算法的步骤如下:

1) 从 FI 输入 w 个记录到工作区 WA。

2) 从 WA 中选出其中关键字取最小值的记录，记为 MINIMAX 记录。

3) 将 MINIMAX 记录输出到 FO 中去。

4) 若 FI 不空，则从 FI 输入下一个记录到 WA 中。

5) 从 WA 中所有关键字比 MINIMAX 记录的关键字大的记录中选出最小关键字记录，作为新的 MINIMAX 记录。

6) 重复 3)~5)，直至在 WA 中选不出新的 MINIMAX 记录为止，由此得到一个初始归并段，输出一个归并段的结束标志到FO中去。

7) 重复 2)~6)，直至 WA 为空。由此得到全部初始归并段。

设待排文件 FI={17,21,05,44,10,12,56,32,29}，WA 容量为3，排序过程如表 8.2 所示。

上述算法，在 WA 中选择 MINIMAX记录的过程需利用败者树来实现。

5.最佳归并树

文件经过置换-选择排序后，得到的是长度不等的初始归并段。

下面讨论如何组织长度不等的初始归并段的归并顺序，使得 I/O 次数最少。

假设由置换-选择排序得到 9个初始归并段，其长度(记录数)依次为9,30,12,18,3,17,2,6,24。

现做 3 路平衡归并，其归并树如图 8.18 所示。

在图 8.18中，各叶结点表示一个初始归并段，上面的权值表示该归并段的长度，叶结点到根的路径长度表示其参加归并的趟数，各非叶结点代表归并成的新归并段，根结点表示最终生成的归并段。

树的带权路径长度 WPL为归并过程中的总读记录数，所以I/O 次数=2xWPL=484。

5.1构造三叉哈夫曼树及相关的分析和计算(2013)

显然，归并方案不同，所得归并树不同，树的带权路径长度(I/O次数)亦不同。

为了优化归并树的 WPL，可以将哈夫曼树的思想推广到 m 又树的情形，在归并树中，让记录数少的初始归并段最先归并，记录数多的初始归并段最晚归并，就可以建立总的 I/O 次数最少的最佳归并树。

上述 9 个初始归并段可构造成一棵如图 8.19 所示的归并树，按此树进行归并，仅需对外存进行446 次读/写，这棵归并树便称为最佳归并树。

图 8.19 中的哈夫曼树是一棵严格 3 叉树，即树中只有度为 3 或 0 的结点。

若只有8个初始归并段，如上例中少了一个长度为 30 的归并段。

若在设计归并方案时，缺额的归并段留在最后，即除最后一次做二路归并外，其他各次归并仍是 3 路归并，此归并方案的 I/O 次数为 386。

显然这不是最佳方案。

正确的做法是：若初始归并段不足以构成一棵严格 k 叉树(也称正则 k 叉树)时，需添加长度为 0的“虚段”，按照哈夫曼树的原则，权为0的叶子应离树根最远。

因此，最佳归并树应如图 8.20 所示，此时的 I/O 次数仅为 326。

如何判定添加虚段的数目?

设度为 0 的结点有 $n_0$ 个，度为k的结点有 $n_k$ 个，归并树的结点总数为n，则有:

$n=n_k+n_0$ (总结点数 = 度为k的结点数 +度为 0 的结点数)
$n=kn_k+1$ (总结点数 = 所有结点的度数之和+1)

因此，对严格 k 叉树有 $n_0=(k-1)n_k+1$ ，由此可得 $n_k=(n_0-1)/(k-1)$ 。

若(n0-1)%(k-1)=0(%为取余运算)，则说明这n0个叶结点(初始归并段)正好可以构造 k 叉归并树。此时，内结点有 $n_k$ 个。

若(n0-1)%(k-1)=u≠0，则说明对于这 n0个叶结点，其中有u个多余，不能包含在 k叉归并树中。

为构造包含所有 n0 个初始归并段的 k 叉归并树，应在原有 $n_k$ 个内结点的基础上再增加 1 个内结点。

它在归并树中代替了一个叶结点的位置，被代替的叶结点加上刚才多出的 u 个叶结点，即再加上k-u-1个空归并段，就可以建立归并树。

5.2实现最佳归并时需补充的虚段数量的分析(2019)

以图 8.19 为例，用 8 个归并段构成 3 叉树，(n0-1)%(k-1)=(8-1)%(3-1)=1，说明7个归并段刚好可以构成一棵严格 3叉树(假设把以5为根的树视为一个叶子)。

为此，将叶子5变成一个内结点，再添加 3-1-1=1个空归并段，就可以构成一棵严格3叉树。